Hello.

I fight this problem already long time.

As we know naive z coordinate reconstruction from x and y coordinates doesn't work properly since there is a sign loss.

That is why i use cry engine approach:

The formulas are very simple:

Normal to GBufffer:

G=normalize(N.xy)*sqrt(N.z*0.5+0.5)

GBuffer to Normal:

N.z=length2(G.xy)*2-1

N.xy=normalize(G.xy)*sqrt(1-N.z*N.z)

I checked it in python and it gives very small error for normalized normal vector - 8.0e-07

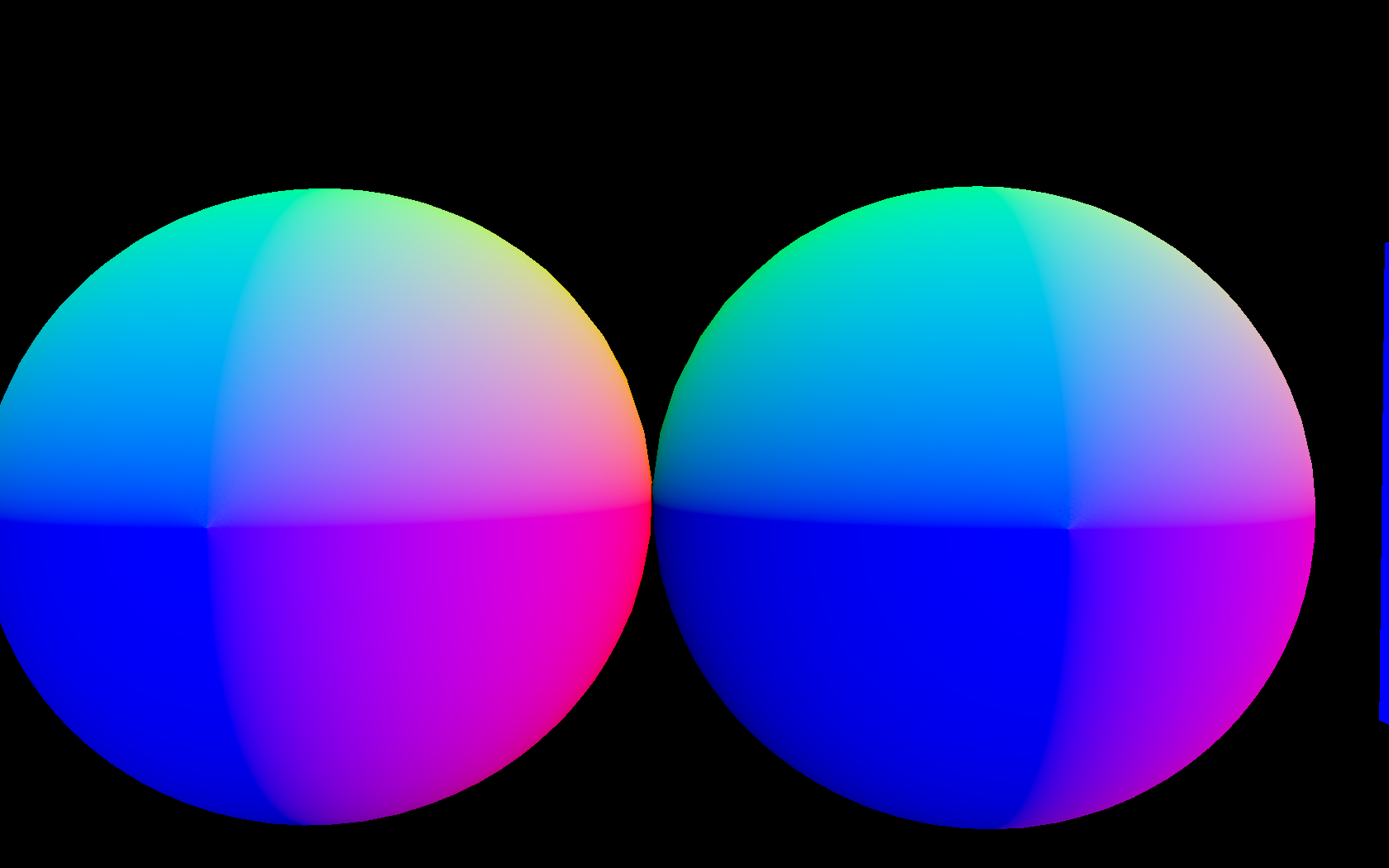
But the image with this approach has visible problem. It looks like there is a cone for some reason.

You can see in the center of sphere there is a cone that has right direction.

I use RGBA16F texture format for framebuffer. There is no such artefacts if i use 3 components normal. Any ideas what can cause such strange effect?

Here are normal map images.

original 3 component normal.

2 component normal with decoding.

It is almost same as above but we can see a cone in the sphere center.

Looks like all compact algorithms have some errors and they are quite visible at some circumstances.

Here is image of “Spherical Coordinates” algorithm.

Looks like i cannot use any compact algorithm if i strive for the best quality possible.

_Flame_ said:
G=normalize(N.xy)*sqrt(N.z*0.5+0.5)

Given the above formula, I would expect an artifact at N.xy = (0, 0), since you can't normalize a zero vector. This seems consistent with your images, where the problem seems to be concentrated at a single point. Have you tried testing if the normalization yields a zero vector, and substituting an arbitrary unit vector for the zero vector if it does?

Have you read this? https://aras-p.info/texts/CompactNormalStorage.html

The way you typically reconstruct a two-component normal (typically screen space) is to assume a value for the Z coordinate. Somewhere between 0.1 and 1.0, depending on whether you need more “oomph” at the very steep edges, or detail at the center. You construct by doing:

G.xy = N.xy * 0.5/max(N.z, 0.00001)

Then reconstruct by doing:

N = G; N.z = 0.5; N = normalize(N);

or, alternatively, simply recover Z assuming x/y are unwarped:

G.xy = N.xy

N.z = 1.0 - sqrt(dot2(N.xy, N.xy));

In screen space, there is no sign loss – you will never see a normal pointed into the screen, because those are away-facing. If you use normal maps, there may be an artifact around the edges of objects, but that artifact is there no matter what, in one way or another.

a light breeze said:

_Flame_ said:
G=normalize(N.xy)*sqrt(N.z*0.5+0.5)

Given the above formula, I would expect an artifact at N.xy = (0, 0), since you can't normalize a zero vector. This seems consistent with your images, where the problem seems to be concentrated at a single point. Have you tried testing if the normalization yields a zero vector, and substituting an arbitrary unit vector for the zero vector if it does?

Indeed. A condition would be enough to solve this problem but it is better not to have it. I'm wondering if in the cry engine this issue is addressed. Thanks for pointing the source of the problem.

hplus0603 said:

The way you typically reconstruct a two-component normal (typically screen space) is to assume a value for the Z coordinate. Somewhere between 0.1 and 1.0, depending on whether you need more “oomph” at the very steep edges, or detail at the center. You construct by doing:

G.xy = N.xy * 0.5/max(N.z, 0.00001)

Then reconstruct by doing:

N = G; N.z = 0.5; N = normalize(N);

or, alternatively, simply recover Z assuming x/y are unwarped:

G.xy = N.xy

N.z = 1.0 - sqrt(dot2(N.xy, N.xy));

In screen space, there is no sign loss – you will never see a normal pointed into the screen, because those are away-facing. If you use normal maps, there may be an artifact around the edges of objects, but that artifact is there no matter what, in one way or another.

Yes i was wondering why should i have any problem in a view space. The fist approach is clever but probably it has errors too. I will try to use the second one.