11 minutes ago, LorenzoGatti said:

In your original example, the formation doesn't fit through the gaps: for instance, 4 and then 2 hit a X on their right as V enters the gap as drawn in the third figure. What are the exact constrains your formation need to obey? How large can they be?

Since the map appears to be quite static, you could precompute pathfinding graphs for different formation shapes (i.e. the leader can walk into an adjacent walkable cell only if the other formation members can walk into the respective offset cells). It would be easy, exact, and cheap unless you have too many formation types for your memory budget or really huge maps.

I think at least some of this has been addressed (or at least discussed) in the thread. Regarding formations fitting through gaps, the formations can fit through even one-cell-wide gaps (see the video for an example) - it's just that that's intended to be a last resort.

As for precomputing information for different formation shapes, I think the complexity there is that (as mentioned above) formations aren't limited by their shape, so you can't necessarily use (e.g.) a naive clearance algorithm. The complexity is that formations can traverse any path, but should prefer paths for which the formation isn't significantly compromised. That seems to be the particular complexity that Rammschnev is trying to address.

Also, I did suggest preprocessing earlier, but in this case that's complicated by the fact that the map may have dynamic obstacles.

Hey all, big thanks for all the responses and ideas, definitely more help than I figured I would get. The weekend has passed, so it's harder for me to spend a lot of time on this, but I want to hit on some general points from the responses, in no particular order:

• Big point of importance here, the number of possible formation configurations is essentially unlimited. The only rule is that the leader needs one empty space around itself in each direction. Anything else goes, no limits on size and no limits on how far apart units can be. This opens the door to a lot of stupid and game-breaking possibilities when the player creates new formations, and I imagine this could be very confusing to the average player who doesn't understand the underlying mechanics of the game. I wouldn't design things this way if the final product was really intended for anyone other than me. I plan to make the game available to play, but the goal is to enjoy playing the game myself and really nothing else, so I accept the complexities that come with that choice. It's basically the essential core mechanic of the game. Everything else is fairly basic. Anyway, point being, all of the algorithms involved in formation behavior need to be extremely flexible.
• Using a distance field is an approach I tried, and while I did not profile to get a specific difference in time, it was noticeably more expensive than the current approach, although there could be a way to improve the speed of that, which is something I will think on. I will also profile it alongside the current when I get a chance. The advantage that the current approach has is that, in most cases, it will not do calculations on the entirety of the map, even if it still does on quite a large portion of it. Using a distance field requires running the clear_area function a number of times equal to the area of the map, which is currently 1500 and I would like to increase when/if I get this issue sorted out. A little more on this in the next point.
• On the point that my map looks fairly static, from which it follows that preprocessing could play an important role, this is a testing map which is not reflective of what a typical encounter will look like. Depending on how large I can get the maps while maintaining performance, I expect 10 - 25 times the number of units running around the map, and I have been working on the assumption so far that all units not in the given formation need to be treated as obstacles during pathfinding. However, your points lead me to consider the possibility that this might not be a necessary assumption, and if I in fact can treat the map as static, only considering the obstacles which do not move, without creating new behavior problems, then I can have a single distance field which updates only in the rare case that a new static obstacle is added to the map, and that would pretty much solve my issue. Will definitely be thinking about this one.
• Thanks to @Andor Patho for introducing me to the concept of morphological erosion. When I first set out to work on this algorithm, I wanted a concept like this but didn't know how to search for it. I'm thinking it probably isn't the solution here, since we are talking about a number of iterations equal to the area of the map (again, currently 1500) * the number of different structuring elements I need to try. I'm still considering ways I could adapt the idea though, so it could end up being something I use.
• When I get some time this week, I will do some proper profiling so we can all be more certain about where specifically the slowdown is happening, but I will note that I am confident that the issue isn't in the implementation of my A*, as I have done nothing but crank out slightly different versions of A* with no significant differences in the core logic/methods for the past 6 weekends that behave much better than this. Knowing that the algorithm in question considers ~1300 out of ~ 1400 possible nodes in the worst cases makes it pretty clear to me that the issue is strictly in the volume of nodes I'm considering combined with the extra calculations to calculate the c_cost. Also, I did profile the clear_area and c functions at one point, and I can't remember their specific values anymore, but they were very small. I believe the issue is running what is otherwise a very efficient calculation 1300 times in a single frame, alongside the regular A* calculations.

Thanks again to everyone for the suggestions and insight! I'll be updating when I can

One thing you might not have considered yet, is that precomputing the "distance field" or in your case the clear_area function for static obstacles does not mean you cannot consider dynamic obstacles as well. Note, that dynamic obstacles have a localised effect on the distance field. That means you can take the static precomputed field, make a copy of it, recompute or adjust values only in the vicinity of dynamic obstacles, and then use it for pathfinding. That way, instead of map_size number of calculations of clear_area, you do unit_count * unit_influence_area calculations per turn, which should be a much lower number hopefully. Also, just to point this out, if multiple leaders are doing pathfinding in the same turn (which I'm still not sure happens in you game), you can fully reuse the precomputed + adjusted map for each of them (with maybe some minor adjustments so they don't consider their own formation as an obstacle, but I'm sure this can be solved reasonably easily).

Maybe this is outside of what you want to do or can do, but have you thought of writing the pathfinding bit in C or C++ to increase the speed?  If you're interpreting Python, it should definitely be a speed up, but if you're compiling python, maybe there won't be as much an improvement, but it was just a thought. 

I know, in general C++ is much faster than python 

https://benchmarksgame-team.pages.debian.net/benchmarksgame/fastest/gpp-python3.html

In the CPython reference implementation, each atomic integer is an independent object with a pointer to the type definition. This is how the language can execute without static type safety, but also makes it thousands of times slower compared to hand optimized assembly. The way you're supposed to use Python is to let another language do the heavy lifting. This takes away the major bottleneck and reduces the number of virtual instructions being executed in the huge switch statement running CPython.

* If you work mostly with low resolutions and are fine with fixed functions, take a look at OpenCV which is made for computer vision but also useful for graphical effects and AI. It comes with the ability to load and execute deep learning models from popular frameworks.
* If you want more performance and the ability to write own image filters, use a framework based on OpenCL. The overhead of Python will be insignificant if you give the GPU a heavy workload. OpenCL is a highly advanced library even for senior professionals, so look for a user friendly abstractions that fit your use case.
* If you want more speed without messing around with libraries, you can also look at other high-level languages that are compiled instead of interpreted. Static type safety may feel like a burden at first but it reduces the time spent on debugging when you catch errors earlier.
* If you don't mind going overkill while learning, you can learn SIMD intrinsics for C/C++ and get a 10000X performance boost without GPU dependencies.

Hey fam, very excited to say I've worked out a solution that's working perfectly, although it still needs some stress testing as it came together very late last night and I went to sleep in victory. I'll update with details tonight. Didn't happen exactly the way I thought it would, but it wouldn't have been possible without the help here, so big thanks to everyone!

So there's an interesting twist to the story of this algorithm: I'm not 100% sure why it works. It will probably make sense when I've actually had some time to look back over it, but the thing is, I stumbled upon the solution while writing messy code after about 5 drinks (I made a backup first, of course), and whatever makes this work, I don't think I would ever have tried it on purpose.

If you're not interested in the narrative, the short version is what I needed was very simple all along: just a slightly modified brushfire algorithm that only allows the node(s) with highest clearance to continue expanding its neighbors. Code and images are below.

So first, when I set out working yesterday morning, I refactored and wrote functions for generating and updating both static and dynamic 'clearance' and 'distance' maps, in my terminology, distance referring to the number of square rings around a position before hitting an obstacle or edge of world and clearance referring to the total clear area enclosed within the largest of those square rings. Clearance is a lot more helpful for the end purpose, distance is helpful for updating the clearance map locally rather than generating a whole new one, as suggested earlier in the thread. That code has done what it needs to from the beginning and stuck around through the rest of my experimenting.

When I set about reworking the algorithm itself, I first tried the approach that I previously said was most promising, simply adding in the precomputed maps to the existing algorithm, requesting a map adjusted for dynamic obstacles at the time the algorithm is run. It did produce correct results and did result in a speedup, but only a very small one, roughly 0.4 seconds, better than nothing but not overly helpful.

After this, I tried an approach that created contiguous 'rooms' with edges defined by changes in distance (yes, distance rather than clearance, as the numbers vary much less but are not specific enough to be as helpful as needed, it turns out). I don't think I've ever written more disgusting code, maybe apart from the one time I tried messing around with GL shaders. Suffice it to say, it did not work. Maybe it could have been made to work, but it revealed quickly that, where I had imagined rooms being messy, convex blobs, they more tended to be concave rings that clung to the walls and world edges. One particularly important problem that arises from this is, how would I define the approximate location of a room like this relative to the destination? I was calculating a rough center of mass for each room, but if the room is a thin ring around a wide area, that center of mass has little to do with where that room actually is. Maybe this approach could have been made to work another way, but looking over the data it produced led me to the approach that did end up working.

So as I already mentioned, despite my specific needs being a fairly unique case, a very simple solution that only needed a little tweaking has already existed for a long time, and that is the brushfire algorithm. In its basic form, all a brushfire algorithm does is expand nodes such that all paths considered are kept to the same length until one of them reaches the destination. It doesn't use any heuristic; it just accepts the first path that gets there, relying on the principle that the shortest path will get there first. I'm not an expert on it, but my understanding is that it only considers horizontal and vertical neighbors so that there isn't any consideration of diagonal movement cost, updating existing paths with shorter alternatives, etc. This is actually one of the earliest approaches I considered, long before I posted here, but I shied away from doing it the right way because I thought I would end up having to do weird things to incentivize it to consider diagonal paths correctly and instead put together what essentially amounted to a stupid version of A*. Should have trusted it. It finds diagonal paths just fine, the only thing being that it will produce a 'staircase' type of path, repeatedly moving horizontally and then vertically, since that's all it's allowed to do. The final path just needs some smoothing, and it's perfect.

Where my implementation differs is that, rather than keeping all path lengths consistent, it only allows the node with the highest clearance to expand. This still means a lot of nodes are considered, but there is essentially no calculation to be done on them apart from acknowledging that they exist and adding them to a few lists. Paths stop expanding at narrow passages and continue when no higher-clearance options are available. It's pretty simple, ultimately; I just wasn't thinking about it the right way from the start.

So now it's time for the actual results. On my worst-case-scenario map, shown below, I've gotten a speedup from 1.99 seconds with the A* approach down to 0.13 seconds with the brushfire approach, less than 10% of the original runtime. Perfect. This is now something I can confidently allow to run multiple times in a frame in the course of a complicated game with lots of player and AI formations running around.

Here is the code that finally freed me from this mental prison, although it will probably be ever so slightly tweaked when I understand the anomaly I will explain shortly:

static_clearance_map = [[0 for y in range(game_height)] for x in range(game_width)]
static_distance_map = [[0 for y in range(game_height)] for x in range(game_width)]
# Distance in this context refers to the number of square rings around the given position until an obstacle is hit
# We use this information to update only necessary parts of static_clearance_map when new static objects are spawned

def update_static_maps():

    global static_clearance_map
    global static_distance_map

    write_log('updating static maps globally')

    for x in range(game_width):
        for y in range(game_height):
            area, distance = clear_area_and_distance_static((x, y))
            static_clearance_map[x][y] = area
            static_distance_map[x][y] = distance

    write_numeric_2D_list_to_file(static_clearance_map, 'static_clearance')
    write_numeric_2D_list_to_file(static_distance_map, 'static_distance')


def update_static_maps_local_to(position):

    global static_clearance_map
    global static_distance_map

    write_log('updating static maps locally')

    positions_to_update = [position]

    distance = 0
    new_positions_found = True
    while new_positions_found:

        distance += 1
        corner_a = (position[0] - distance, position[1] - distance)
        corner_b = (position[0] + distance, position[1] + distance)
        ring = rectline(corner_a, corner_b)

        new_positions_found = False
        for point in ring:

            if not within_game_bounds(point):
                continue

            distance_at_point = static_distance_map[point[0]][point[1]]
            x_diff = abs(position[0] - point[0])
            y_diff = abs(position[1] - point[1])

            if x_diff <= distance_at_point and y_diff <= distance_at_point:
                positions_to_update.append(point)
                new_positions_found = True

    updated_positions = [[0 for y in range(len(static_clearance_map[0]))] for x in range(len(static_clearance_map))]

    for pos in positions_to_update:

        updated_positions[pos[0]][pos[1]] = 1

        area, distance = clear_area_and_distance_static(pos)
        static_clearance_map[pos[0]][pos[1]] = area
        static_distance_map[pos[1]][pos[1]] = distance

    write_numeric_2D_list_to_file(static_clearance_map, 'static_clearance')
    write_numeric_2D_list_to_file(static_distance_map, 'static_distance')
    write_numeric_2D_list_to_file(updated_positions, 'updated_positions')

def clear_area_and_distance_static(position):
    """ Check in square rings around the position for static obstacles/edges of map, then return the total area that is passable
        within the square that first hits an obstacle/edge of map and the size of that square """

    if static_obstacle_at_position(position):
        return (0, 0)

    distance = 0
    hit_obstacle = False
    while not hit_obstacle:
        distance += 1
        corner_a = (position[0] - distance, position[1] - distance)
        corner_b = (position[0] + distance, position[1] + distance)
        ring = rectline(corner_a, corner_b)
        for point in ring:
            if not within_game_bounds(point):
                hit_obstacle = True
                break
            elif static_obstacle_at_position(point):
                hit_obstacle = True
                break

    tent_area = rectfill(corner_a, corner_b)
    area = 0
    for point in tent_area:
        if within_game_bounds(point):
            if not static_obstacle_at_position(point):
                # Some stray diagonals may get counted here occasionally, but that should be acceptable for this purpose
                area += 1

    return (area, distance)

def get_dynamic_clearance_map(treat_passable = [], treat_impassable = []):
    """ Return a modified version of static_clearance_map that accounts for objects that can move (units) """

    global objects
    global static_clearance_map
    global static_distance_map

    dynamic_clearance_map = [static_clearance_map[x][:] for x in range(len(static_clearance_map))]
    dynamic_obstacles = []
    for obj in objects:
        if 'frames_to_move' in obj.keys():
            dynamic_obstacles.append(obj)

    positions_to_modify = treat_passable + treat_impassable

    for obstacle in dynamic_obstacles:

        position = obstacle['position']
        if not position in positions_to_modify:
            positions_to_modify.append(position)

        distance = 0
        new_positions_found = True
        while new_positions_found:

            distance += 1
            corner_a = (position[0] - distance, position[1] - distance)
            corner_b = (position[0] + distance, position[1] + distance)
            ring = rectline(corner_a, corner_b)

            new_positions_found = False
            for point in ring:

                if not within_game_bounds(point):
                    continue

                distance_at_point = static_distance_map[point[0]][point[1]]
                x_diff = abs(position[0] - point[0])
                y_diff = abs(position[1] - point[1])

                if x_diff <= distance_at_point and y_diff <= distance_at_point:
                    if not point in positions_to_modify:
                        positions_to_modify.append(point)
                    new_positions_found = True

    for position in positions_to_modify:

        area = clear_area_and_distance_dynamic(position, treat_passable = treat_passable, treat_impassable = treat_impassable)[0]
        dynamic_clearance_map[position[0]][position[1]] = area

    write_numeric_2D_list_to_file(dynamic_clearance_map, 'dynamic_clearance')
    return dynamic_clearance_map

def get_dynamic_distance_map(treat_passable = [], treat_impassable = []):
    """ Return a modified version of static_distance_map that accounts for objects that can move (units) """

    global objects
    global static_clearance_map
    global static_distance_map

    dynamic_distance_map = [static_distance_map[x][:] for x in range(len(static_distance_map))]
    dynamic_obstacles = []
    for obj in objects:
        if 'frames_to_move' in obj.keys():
            dynamic_obstacles.append(obj)

    positions_to_modify = treat_passable + treat_impassable

    for obstacle in dynamic_obstacles:

        position = obstacle['position']
        if not position in positions_to_modify:
            positions_to_modify.append(position)

        distance = 0
        new_positions_found = True
        while new_positions_found:

            distance += 1
            corner_a = (position[0] - distance, position[1] - distance)
            corner_b = (position[0] + distance, position[1] + distance)
            ring = rectline(corner_a, corner_b)

            new_positions_found = False
            for point in ring:

                if not within_game_bounds(point):
                    continue

                distance_at_point = static_distance_map[point[0]][point[1]]
                x_diff = abs(position[0] - point[0])
                y_diff = abs(position[1] - point[1])

                if x_diff <= distance_at_point and y_diff <= distance_at_point:
                    if not point in positions_to_modify:
                        positions_to_modify.append(point)
                    new_positions_found = True

    for position in positions_to_modify:

        distance = clear_area_and_distance_dynamic(position, treat_passable = treat_passable, treat_impassable = treat_impassable)[1]
        dynamic_distance_map[position[0]][position[1]] = distance

    write_numeric_2D_list_to_file(dynamic_distance_map, 'dynamic_distance')
    return dynamic_distance_map

def clear_area_and_distance_dynamic(position, treat_passable = [], treat_impassable = []):
    """ Check in square rings around the position for all obstacles/edges of map, then return the total area that is passable
        within the square that first hits an obstacle/edge of map and the size of that square """

    if (not position_is_passable(position)) and (not position in treat_passable):
        return (0, 0)

    distance = 0
    hit_obstacle = False
    while not hit_obstacle:
        distance += 1
        corner_a = (position[0] - distance, position[1] - distance)
        corner_b = (position[0] + distance, position[1] + distance)
        ring = rectline(corner_a, corner_b)
        for point in ring:
            if not within_game_bounds(point):
                hit_obstacle = True
                break
            elif (object_at(point) is not None) or (point in treat_impassable):
                if not point in treat_passable:
                    hit_obstacle = True
                    break

    tent_area = rectfill(corner_a, corner_b)
    area = 0
    for point in tent_area:
        if within_game_bounds(point):
            if (object_at(point) is None) or (point in treat_passable):
                # Some stray diagonals may get counted here occasionally, but that should be acceptable for this purpose
                if not point in treat_impassable:
                    area += 1

    return (area, distance)

def leader_pathfind(leader, going_to, treat_passable = [], treat_impassable = []):

    global formation_dict

    at_now = leader['position']

    if at_now == going_to:
        return []

    treat_passable.append(going_to) # Prevents indefinite hanging while rerouting if an obstacle has moved to the destination

    formation_obj = formation_dict[leader['id']]
    vectors = formation_obj.get_formation_vectors()
    optimal_distance = 0
    for vector in vectors:
        for axis in vector:
            if abs(axis) > optimal_distance:
                optimal_distance = abs(axis)

    dynamic_clearance_map = get_dynamic_clearance_map(treat_passable = treat_passable, treat_impassable = treat_impassable)

    def c(position):
        if within_game_bounds(position):
            distance = dynamic_clearance_map[position[0]][position[1]]
            return distance
        else:
            raise ValueError('leader_pathfind: c: position ' + str(position) + ' not in game bounds')

    c_dict = {at_now: c(at_now)}
    g_dict = {at_now: 0}

    open_set_this_frame = [at_now]
    open_set_next_frame = []
    closed_set = []
    get_last = {}

    c_threshold = c_dict[at_now]
    highest_c_last_frame = c_dict[at_now]

    search_map = [[0 for y in range(game_height)] for x in range(game_width)] # This is just for visualizing the algorithm's behavior

    found_path = False
    while len(open_set_this_frame) > 0:

        if highest_c_last_frame != c_threshold:
            c_threshold = highest_c_last_frame
            
        write_log('leader_pathfind: main while: highest_c_last_frame and therefore c_threshold is ' + str(c_threshold))

        highest_c_last_frame = 0

        current = open_set_this_frame[0]
        for op in open_set_this_frame:

            if op == going_to:
                found_path = True
                current = op
                break

            if c_dict[op] > c_dict[current]:
                current = op

        if current == going_to:
            found_path = True
            break

        open_set_this_frame.remove(current)

        if c_dict[current] > highest_c_last_frame:
            highest_c_last_frame = c_dict[current]

        if c_dict[current] > c_threshold:
            open_set_next_frame.append(current)
            write_log('leader_pathfind: --- --- delaying current ' + str(current) + ' with c = ' + str(c_dict[current]) + ' compared to c_threshold = ' + str(c_threshold))
            pass #continue
        write_log('leader_pathfind: --- --- accepting current ' + str(current) + 'with c = ' + str(c_dict[current]) + ' compared to c_threshold = ' + str(c_threshold))
        
        closed_set.append(current)
        search_map[current[0]][current[1]] = g_dict[current]

        write_log('leader_pathfind: main while: considering ' + str(current))

        for neighbor in neighbors_brushfire(current):

            write_log('leader_pathfind: --- --- considering neighbor ' + str(neighbor) + ' of original ' + str(current))

            if not within_game_bounds(neighbor):
                continue
            if neighbor in closed_set:
                if neighbor == going_to:
                    write_log('leader_pathfind: destination ' + str(going_to) + ' has been found in closed_set')
                continue
            if neighbor in open_set_this_frame:
                if neighbor == going_to:
                    write_log('leader_pathfind: destination ' + str(going_to) + ' has been found in open_set_this_frame')
                continue
            if neighbor in open_set_next_frame:
                if neighbor == going_to:
                    write_log('leader_pathfind: destination ' + str(going_to) + ' has been found in open_set_next_frame')
                continue

            tent_c = c(neighbor)
            if tent_c == 0:
                continue

            tent_g = g_dict[current] + 1

            open_set_next_frame.append(neighbor)
            c_dict[neighbor] = tent_c
            g_dict[neighbor] = g_dict[current] + 1
            get_last[neighbor] = current

            if neighbor == going_to:
                write_log('leader_pathfind: destination ' + str(going_to) + ' has been added to open_set_next_frame in the usual way')

        open_set_this_frame, open_set_next_frame = open_set_next_frame, open_set_this_frame

    write_numeric_2D_list_to_file(search_map, 'search_map')

    if found_path:

        path = [going_to]
        current = path[-1]
        while current != at_now:
            current = get_last[current]
            path.append(current)

        path.reverse()
        path.pop(0)
        return path

    else:
        write_log('leader_pathfind: could not find path from ' + str(at_now) + ' to ' + str(going_to))
        return False

(I've forgotten to mention, my code is in Python 2.7, not the most current version, which is not ideal and honestly wasn't on purpose.)

Here is my worst-case scenario map, which I call 'bottleneck:'

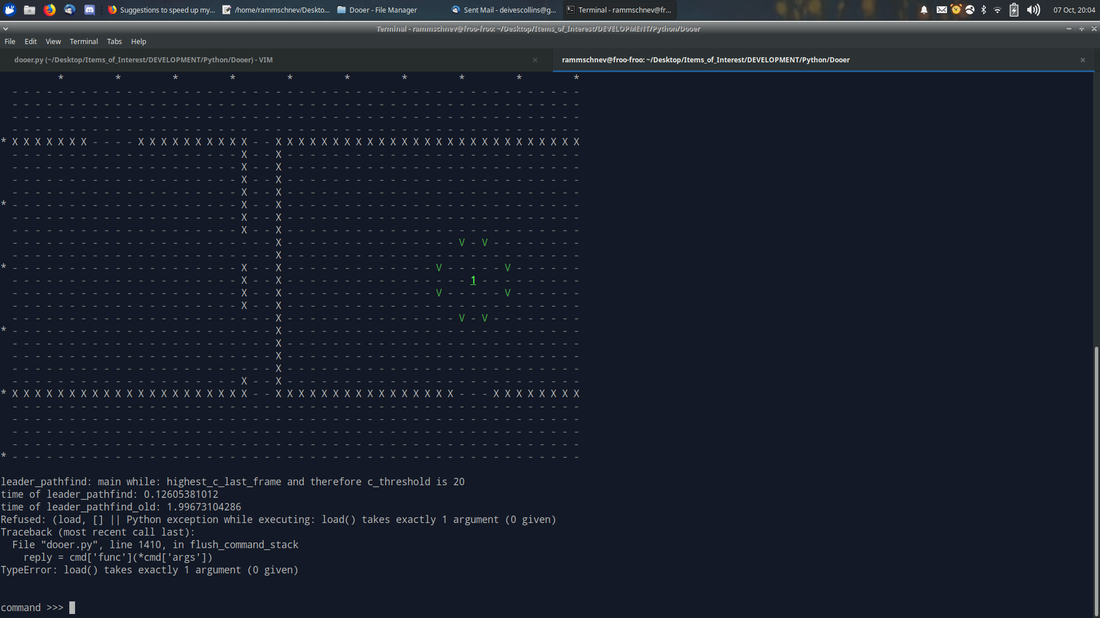
Here is the path we want returned by the algorithm (assuming diagonal smoothing has taken place):

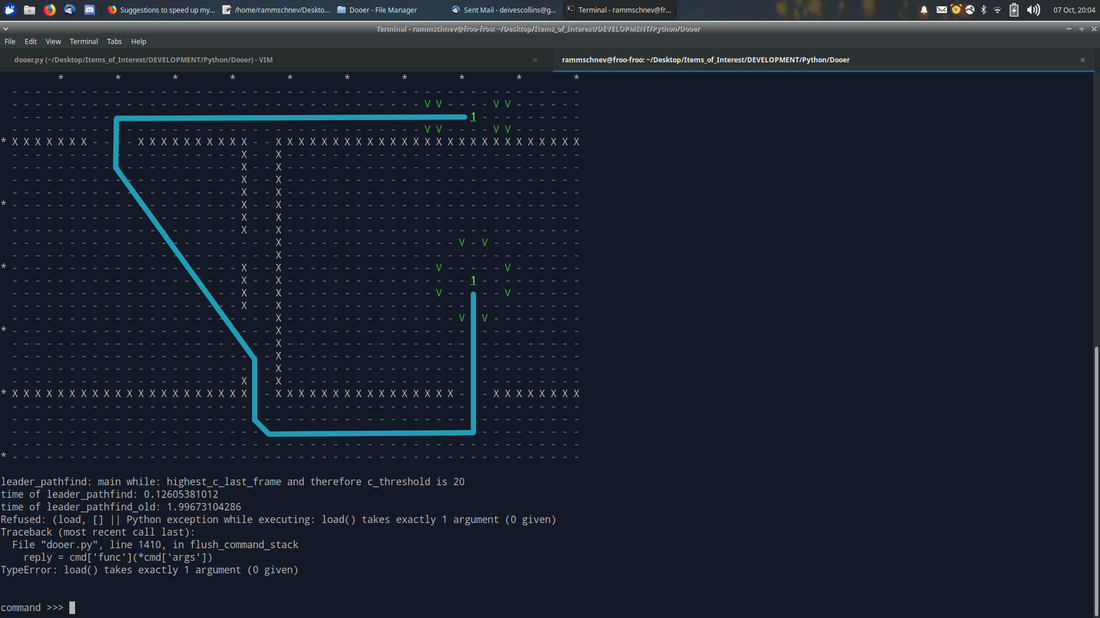
Here is a visualization of what the algorithm considers, where the value of a cell represents how many steps have been taken to find that cell. Only considered (expanded) nodes get a value, not neighbors awaiting consideration.

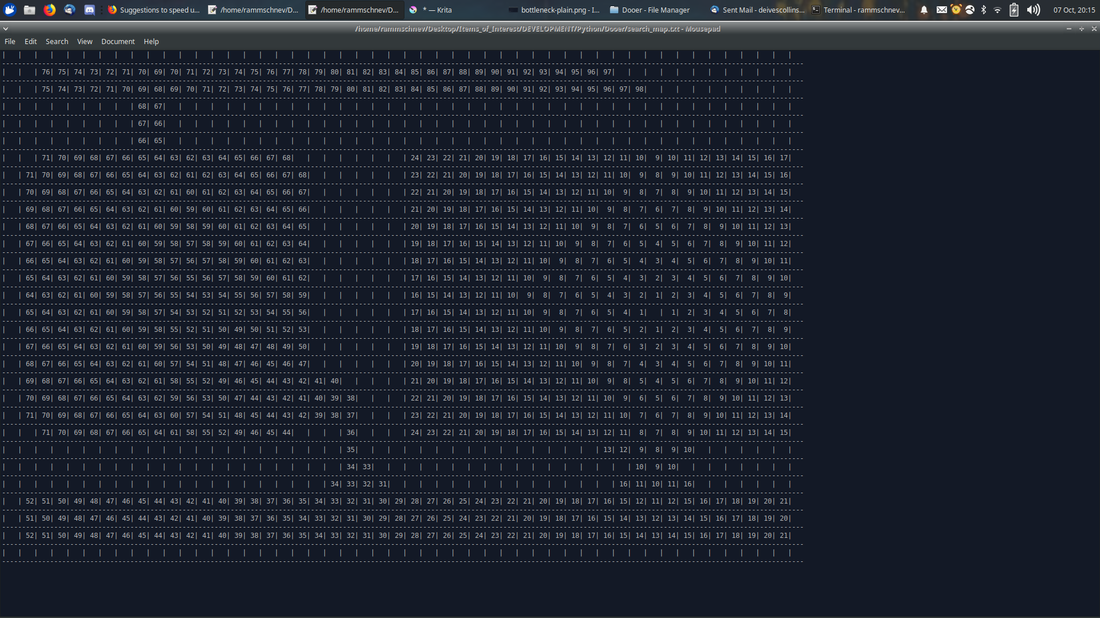
And this is the clearance map which the algorithm used to produce these results:

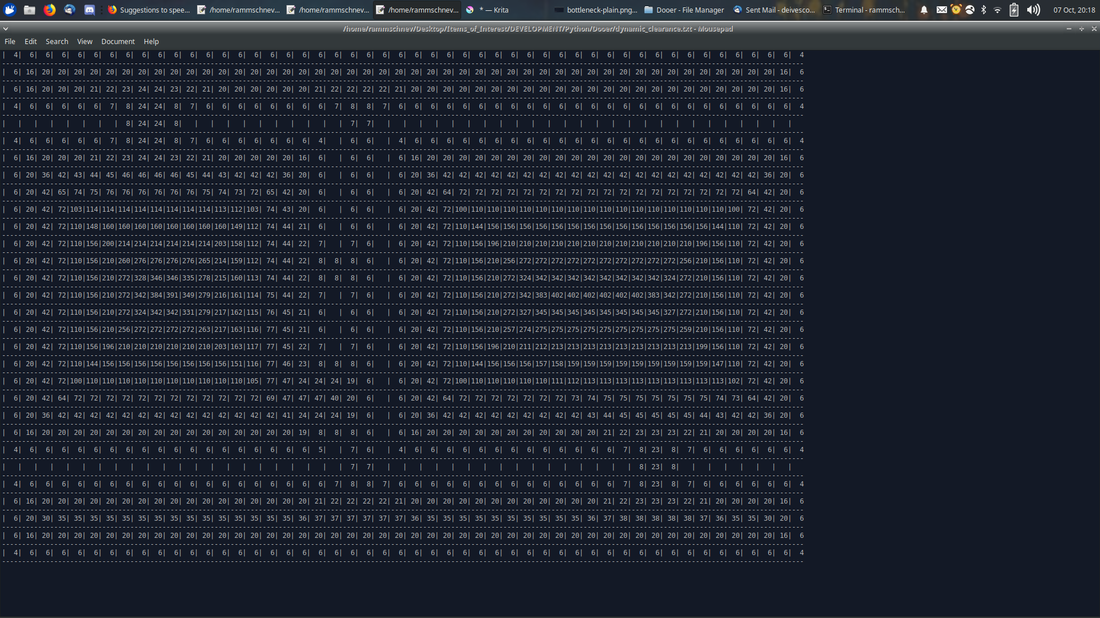
So there's what's important. It works and performs beautifully. I could leave this alone and move on, if I didn't consider it important to understand what serendipitously went right in my final algorithm. Read on if you want to know about that.

What the algorithm actually does is pretty close to what I meant for it to do when writing it. However, rather than considering the node with the very highest clearance every iteration, I meant to identify a batch of acceptable nodes above a certain clearance threshold (c_threshold), bump rejected nodes into a second set along with discovered neighbors that would move up to first priority next frame** (and continue to bump them for however long they remain below the changing threshold), and create a new empty list to replace the second set once it gave up its contents to the first list. Solely for the purpose of recycling memory, instead of actually creating a new lists, I intended to swap the values of the first and second lists once the first was empty. We see this happen at line 356 of the above code:

** It's misleading of me to use the term 'frame' here. I'm not talking about frames in the context of the execution of the game, but rather treating each batch of nodes as a 'frame'

        open_set_this_frame, open_set_next_frame = open_set_next_frame, open_set_this_frame

If you're not familiar with Python, this operation swaps the value of two variables without the need to create a third temporary variable.

What I failed to do was have this happen only when the first list (open_set_this_frame) was empty. Instead, this happens every iteration. Meanwhile, I also accidentally bumped nodes with values above rather than below the c_threshold into the second list, which you can see at line 312:

        if c_dict[current] > c_threshold:
            open_set_next_frame.append(current)
            write_log('leader_pathfind: --- --- delaying current ' + str(current) + ' with c = ' + str(c_dict[current]) + ' compared to c_threshold = ' + str(c_threshold))
            pass #continue

Originally the block would continue (i.e. not proceed with considering this node) rather than simply pass (do nothing, effectively just an empty line). Interestingly, the algorithm works either way, although opting to continue rather than pass leaves a few puzzling holes in the search map that I'd rather not have become problems later. However, a consequence of this is that the node gets considered and therefore ends up in the closed_set while also existing in open_set_next_frame, potentially multiple times over. And somehow, this doesn't cause any problems.

So instead of dealing with a batch of nodes and choosing from it the node with the highest_c above the c_threshold, the algorithm chooses the node with the highest clearance each iteration and bounces between two fluctuating open sets full of duplicates. Before writing this, I spent a quick minute in a more sober state of mind tweaking the code to run the way I originally intended it to, and for reasons I've not yet taken the time to determine, the algorithm in fact fails altogether that way. It also fails if the greater than is changed to a less than in line 312. But by the mysterious hand of fate, as it stands now, it serves all my needs, and only my curiosity keeps me bound to ever looking at it again.

So with that, the case is almost entirely closed. I will post a small update when I figure out what sorcery is at play in those implementation details. If you actually read all of this, you're an athlete and deserve to know it. Big thanks again to everyone who contributed ideas that helped me get here, and hopefully this eventually helps another hobby dev or two down the line.

Thanks for the detailed update ? It's always nice when people report back and share their results in threads like this. (If nothing else, it can be helpful to future readers, as you note.)