I'm working on a step-time strategy game (not sure if that's the proper term, but it moves in discrete time steps, about 4 frames, before pausing for input) with positively monstrous pathfinding calculations. I've solved the biggest of my problems already, but there is one algorithm that causes significant slowdown, and I'm sure it could be optimized, but I'm not sure how best to do that because my case has a unique property that isn't covered in any A* optimizations I've researched. (Or perhaps I'm just not thinking about it the right way.)

My game allows the creation of formations, which are defined as positional groupings of units relative to a leader. It's extremely important to the gameplay that these formations keep their shape as best as possible while balancing the need to move smoothly through any narrow spaces that constrict their shape. The algorithm I'm asking about now is responsible for choosing a path for the leader of the formation that (1) avoids unnecessarily traveling into narrow spaces and (2) always allows a certain amount of clearance between itself and obstacles, whenever those things are possible. Where I have found typical clearance-based approaches to A* fall short in addressing my problem is, ultimately, the leader will choose a path that goes through areas even just 1 space wide if there is no other option. In other words, I can't have the algorithm disregard those, but I can't have it explore those nodes either until it has explored the entirety of the rest of the map.

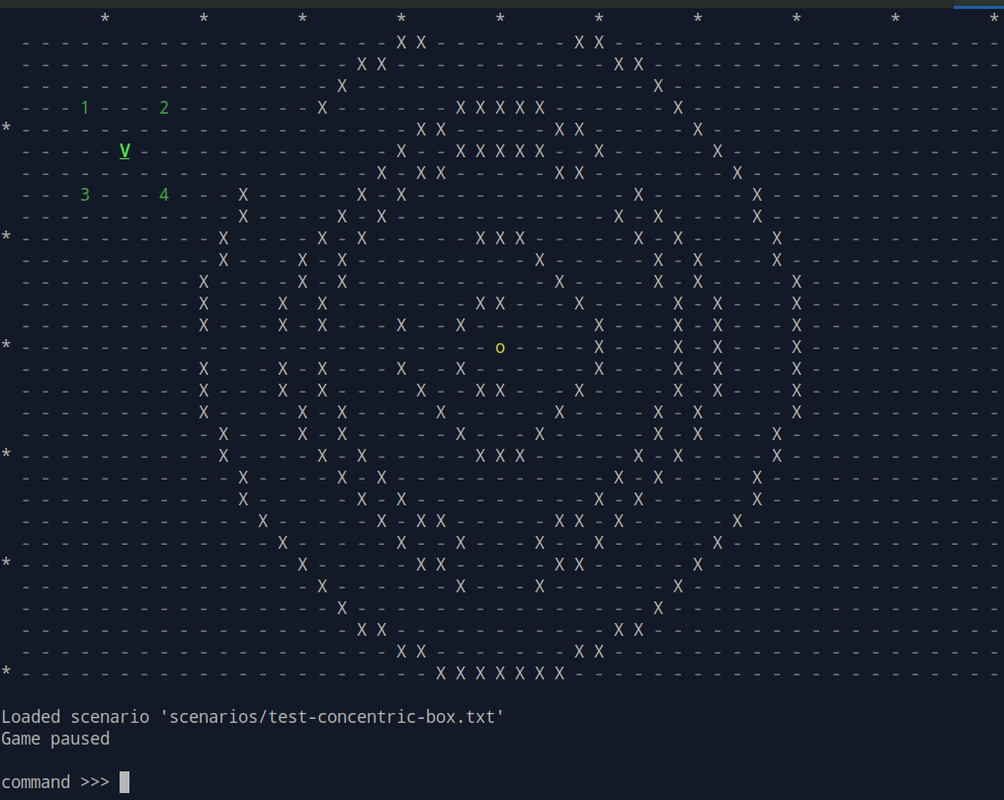
Here is my basic test map for this. The 5 green symbols at the top-left represent a formation led by the V in the center. The yellow circle at the center of the map is the goal.

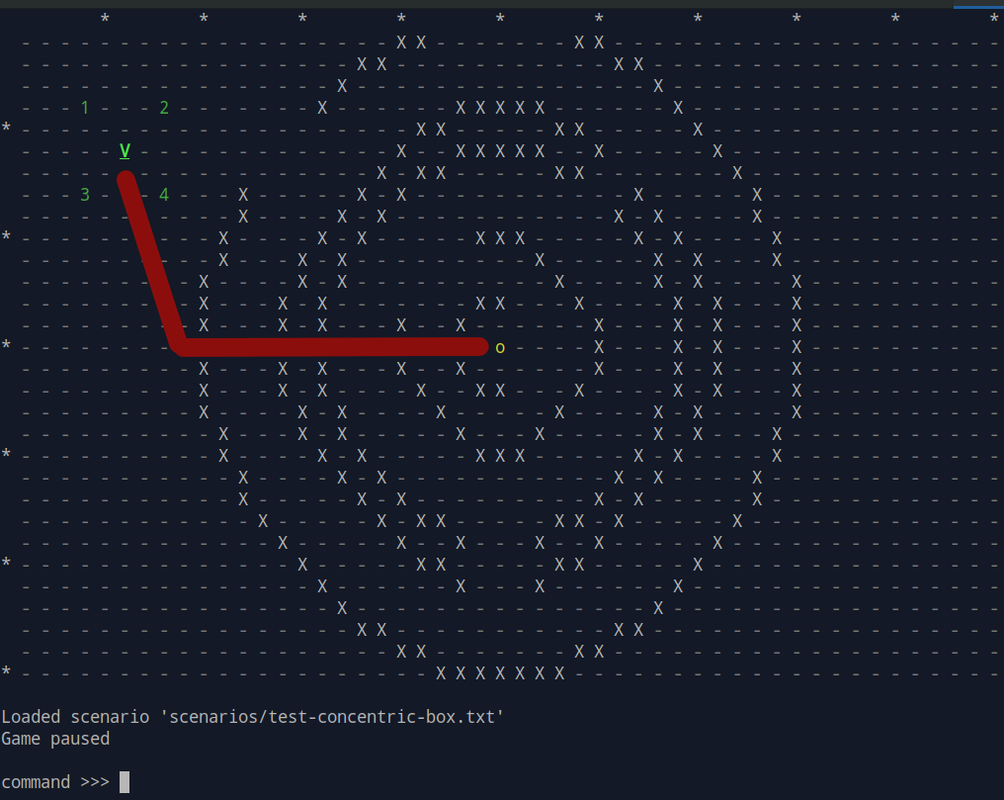
Here is the solution that a regular A* would give, finding the shortest path:

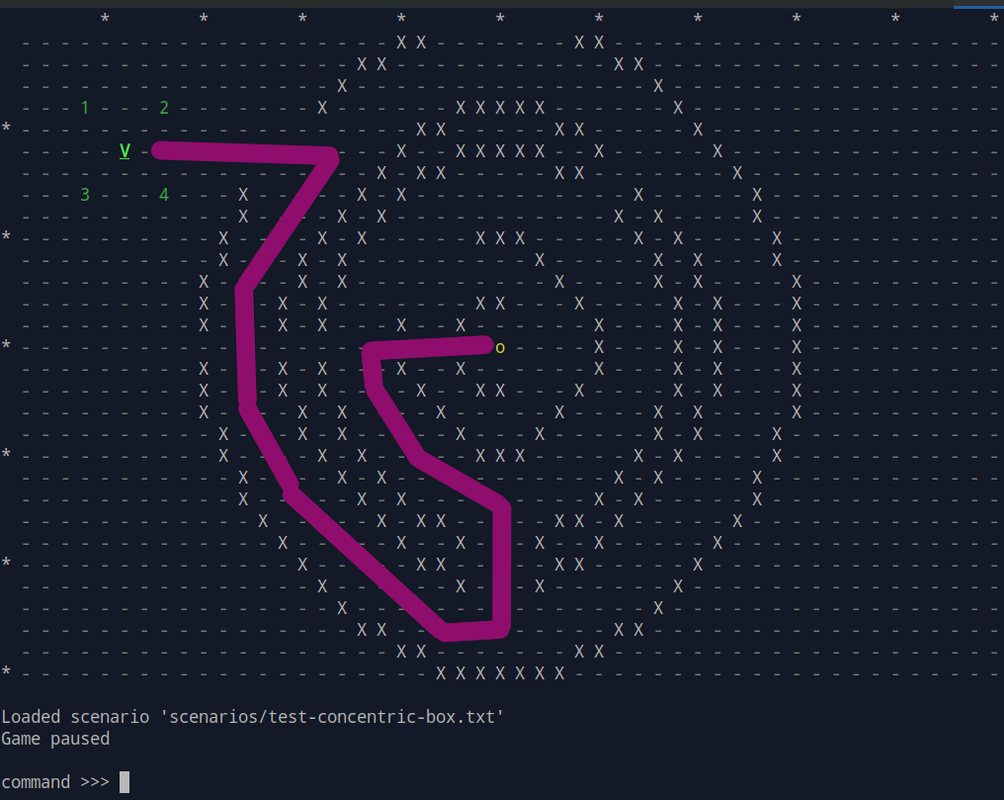
Here is the solution I want (and the algorithm already does this, just slowly)

Here is the Python code that achieves this -- I know there are going to be some questions about what the vectors are and all of that, but basically, this is just a typical A* setup with the addition of a "c_cost," which is 0 if the given node has all the space that it wants (as defined by optimal_area), or 2 ^ the number of spaces missing from the amount of space we want.

def leader_pathfind(leader, going_to, treat_passable = [], treat_impassable = []):
    """ Seek the shorest path that attempts to avoid obstacles at a distance equal to that of the furthest member in the formation """

    global game_width
    global game_height
    global diagonal_movement_cost
    global formation_dict

    at_now = leader['position']

    treat_passable.append(going_to) # Prevents indefinite hanging while rerouting if an obstacle has moved to the destination

    if at_now == going_to:
        return []

    formation_obj = formation_dict[leader['id']]
    vectors = formation_obj.get_formation_vectors()
    max_dimension = 0
    for vector in vectors:
        for axis in vector:
            if abs(axis) > max_dimension:
                max_dimension = abs(axis)
    optimal_area = basic_pow(max_dimension * 2 + 1, 2)

    def clear_area(position):
        """ Check in square rings around the position for obstacles/edges of map, then return the total area that is passable
            within the square that first hits an obstacle/edge of map """

        if not position_is_passable(position, treat_passable = treat_passable, treat_impassable = treat_impassable):
            return sys.maxint

        distance = 0
        hit_obstacle = False
        while not hit_obstacle:
            distance += 1
            corner_a = (position[0] - distance, position[1] - distance)
            corner_b = (position[0] + distance, position[1] + distance)
            outline = rectline(corner_a, corner_b)
            for point in outline:
                if not within_game_bounds(point):
                    hit_obstacle = True
                    break
                elif not position_is_passable(point, treat_passable = treat_passable, treat_impassable = treat_impassable):
                    hit_obstacle = True
                    break
                elif distance == max_dimension: # We have all the space we want, no need to compute further
                    hit_obstacle = True
                    break

        tent_area = rectfill(corner_a, corner_b)
        area = 0
        for point in tent_area:
            if within_game_bounds(point):
                if position_is_passable(point, treat_passable = treat_passable, treat_impassable = treat_impassable):
                    # Some stray diagonals may get counted here occasionally, but that should be acceptable for this purpose
                    area += 1

        return area

    def c(position): # c_cost is in terms of clear area relative to the optimal clearance
        area = clear_area(position)
        c_cost = 0 if area >= optimal_area else basic_pow(2, abs(area - optimal_area)) # Cost grows exponentially by powers of 2 for each point less than the optimal area
        return c_cost

    # Traditional A* #

    def h(position):
        return basic_distance(position, going_to) / 100.0

    f_dict = {at_now: h(at_now)}
    g_dict = {at_now: 0}

    open_set = [at_now]
    closed_set = []
    get_last = {}

    found_path = False
    current = at_now

    while len(open_set) > 0:

        current = open_set[0]

        for op in open_set:
            if op in f_dict.keys():
                if f_dict[op] < f_dict[current]:
                    current = op

        open_set.remove(current)
        closed_set.append(current)

        if current == going_to:
            found_path = True
            break

        for neighbor in neighbors(current, treat_passable = treat_passable, treat_impassable = treat_impassable):

            if neighbor in closed_set:
                continue
            if not neighbor in open_set:
                open_set.append(neighbor)

            movement_cost = diagonal_movement_cost if diagonally_adjacent(current, neighbor) else 1

            tent_g = g_dict[current] + movement_cost
            tent_f = tent_g + c(neighbor) + h(neighbor)
            if not neighbor in f_dict.keys():
                g_dict[neighbor] = tent_g
                f_dict[neighbor] = tent_f
                get_last[neighbor] = current
            else:
                if tent_f < f_dict[neighbor]:
                    g_dict[neighbor] = tent_g
                    f_dict[neighbor] = tent_f
                    get_last[neighbor] = current

    if found_path:

        path = [going_to]
        current = going_to

        while current != at_now:

            current = get_last[current]
            path.append(current)

        path.reverse()
        path.pop(0)
        return path

    else:
        write_log('leader_pathfind: could not find a path from ' + str(at_now) + ' to ' + str(going_to))
        return False

Jump Point Search, which I've used elsewhere, relies on the assumption of a uniform-cost grid, so I believe I need to rely on abstracting my map down to a smaller number of abstract nodes, and I'm at a loss for how I would do that for this case. What I've read on using abstract nodes rely on things like identifying entrances/exits from abstract nodes, but that won't be useful if the algorithm chooses a node with acceptable entrance/exit points but lots of obstacles in the middle. Here is an arbitrarily chosen slice of the map with the correct path:

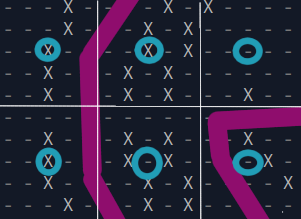
Broken up into abstract 5x5 nodes, I am failing to see a pattern I could rely on to give the algorithm the information it needs, especially since a crucial part of the path rests right on the right edge of the two leftmost abstract nodes. To know that this is the correct path, i.e. has sufficient clearance, it would need to calculate the clearance from that edge, dipping into the nodes in the middle. So I can't choose nodes that will be helpful without already having the information that I need the nodes to speed up the calculation of.

That's as far as I've gotten with my thought process. Can anyone make any suggestions, general or specific? Thanks in advance

I don't have an answer, but that's a very clear and informative post So maybe I can at least help start the discussion.

Quote

Where I have found typical clearance-based approaches to A* fall short in addressing my problem is, ultimately, the leader will choose a path that goes through areas even just 1 space wide if there is no other option. In other words, I can't have the algorithm disregard those, but I can't have it explore those nodes either until it has explored the entirety of the rest of the map.

For some reason I'm having trouble parsing this. Are you saying typical clearance-based algorithms do or do not allow for taking 'narrow paths' if there are no other options?

You said the algorithm finds the desired path, but too slowly. I know this is a prosaic question, but is the slowness due to too many nodes being explored? If so, maybe you've already done this, but it might be interesting to see some analytical graphics showing all the nodes explored for your example path, or even a step-by-step display thereof. Although one can make some guesses about what sort of work the pathfinder is doing, it might be interesting to see it explicitly.

Quote

...but I can't have it explore those nodes either until it has explored the entirety of the rest of the map.

It seems like this could lead to performance problems of its own if there are no 'wide' paths to the goal available. Is that a concern?

Another obvious question, but have you tried making the cost of narrow paths so high that the pathfinder basically has to explore all other options first? (That doesn't address the question of performance problems when no wide paths are available though.)

I'm also wondering if some sort of preprocessing could play a role. I don't know how many formation sizes you have, but assume for the sake of discussion that only one size is needed. My casual observation about your example map is that (or so it seems) there's no cell accessible via the left-center narrow path that isn't accessible via the center-bottom wide path. As such, it seems that narrow path could just be considered solid as far as the pathfinder was concerned. I realize that if the map has dynamic elements it might not be that simple, and I haven't thought through it beyond that simple observation, but it does bring to mind some sort of preprocessing and/or formation-specific metainformation.

I haven't read any literature on clearance-based pathfinding or related topics, and I may be missing the obvious here. In any case, apologies if any of this is unuseful and/or naive, but maybe it'll at least lead to some discussion.

Thanks @Zakwayda for the thoughtful response! I'll go down the line here:

58 minutes ago, Zakwayda said:

Quote

Where I have found typical clearance-based approaches to A* fall short in addressing my problem is, ultimately, the leader will choose a path that goes through areas even just 1 space wide if there is no other option. In other words, I can't have the algorithm disregard those, but I can't have it explore those nodes either until it has explored the entirety of the rest of the map.

For some reason I'm having trouble parsing this. Are you saying typical clearance-based algorithms do or do not allow for taking 'narrow paths' if there are no other options?

Yes, what I was able to find on the subject made the assumption that clearance-based pathfinding was being done for a unit of a set, non-flexible size, which simply would be able to fit through an opening or not. It seems my case is fairly unique in that the size of the formation can be fluid, as the subordinates in the formation are programmed to pack in tighter and move around each other as necessary. If it wouldn't be possible for the formation to get through a tight space whatsoever, then I could treat the extremely narrow openings as off-limits (getting at one of your later questions a little bit). They will get through, but even in a best-case scenario, it will be ugly and inconvenient, stripping the formation of its purpose really until it has a chance to regroup on the other side, and at worst, it can get stuck entirely as the units compete for the same space. These are inherent risks in allowing this much flexibility, which I suspect is a large part of why most strategy genre developers don't try to do this, but having this system of avoiding the tight passages mitigates a lot of that risk unless the map is simply tight all over, which would in turn call for the player to use a different strategy when assembling formations. Managing this risk is part of the gameplay, but it would make things drastically less fun if the player risked losing an encounter over a formation choosing a tight route when a wide open route is available.

1 hour ago, Zakwayda said:

You said the algorithm finds the desired path, but too slowly. I know this is a prosaic question, but is the slowness due to too many nodes being explored? If so, maybe you've already done this, but it might be interesting to see some analytical graphics showing all the nodes explored for your example path, or even a step-by-step display thereof. Although one can make some guesses about what sort of work the pathfinder is doing, it might be interesting to see it explicitly.

Yes, the slowness is without a doubt 100% on account of the large quantity of nodes being explored. I do wish I had foreseen how complex the pathfinding was going to be earlier in the project (I had the blissful fantasy that I could be done with it in an afternoon lol, six weeks ago), because at this point, representing the pathfinding process graphically would be cumbersome on account of how interwoven the various functions are with each other. It is definitely possible, and I would still consider it if I was more in the dark about what's happening, but I have tracked how many nodes the algorithm considers, and in harder cases, it's upwards of 2/3 of the entire map. Vanilla A* (which itself leaves some optimizing to be desired) is an improvement over its predecessors due to the fact that it makes good guesses about which node is the best to consider next and therefore finds the goal with a minimal number of nodes considered, terminating once it's done so. In my case, I very specifically don't want that to happen, because a much nicer path with lower penalties could exist further away, but I am paying a price in performance. I do in fact want it to look at most of the map, but my intuition says there's a better way to do it. It's just fast enough that I would still allow it in the game if I can't improve upon it at all, because this is a big gameplay-changing difference and the slowdown is about 1-2 seconds (in a ~4 fps game) only when a formation initially chooses its path (and if it needs to reroute).

1 hour ago, Zakwayda said:

Quote

...but I can't have it explore those nodes either until it has explored the entirety of the rest of the map.

It seems like this could lead to performance problems of its own if there are no 'wide' paths to the goal available. Is that a concern?

Definitely, these are the cases when the algorithm takes the longest. Even worse when the player tries to move a formation to a space that is not actually reachable.

It's also worth noting that it's a bad idea for a player to try to squeeze a formation, other than a very small one, through tight spaces, and that will be covered in the tutorial. In addition to being able to construct formations of virtually any configuration, the game can be played on maps of virtually any configuration, so an approach that is reasonably prepared for any situation is needed. Smaller formations would have less issues with tight spaces in terms of performance because the penalty will be lower, as it is relative to the distance between the leader and the subordinate furthest away (when the formation was originally formed and its shape was saved).

1 hour ago, Zakwayda said:

Another obvious question, but have you tried making the cost of narrow paths so high that the pathfinder basically has to explore all other options first? (That doesn't address the question of performance problems when no wide paths are available though.)

This is in fact the reason that the c_cost increases exponentially rather than linearly and the h_cost is divided by 100, because it was difficult at first to convince the algorithm that I was serious about my intentions lol. A difference of 5 or 10 in h_cost, fairly standard numbers to expect, was the equal of 2 or 3 squares of reduced area in c_cost, so it was still favoring shorter, tighter paths. The numbers get huge very fast with the exponential approach, so closeness to the goal is almost an afterthought. As I already covered mostly, this is exactly what I want, and the only hope I really have for a speedup is if I can find a clever way to make reliable assumptions about a few nodes at a time rather than evaluating each individual one.

1 hour ago, Zakwayda said:

I'm also wondering if some sort of preprocessing could play a role. I don't know how many formation sizes you have, but assume for the sake of discussion that only one size is needed. My casual observation about your example map is that (or so it seems) there's no cell accessible via the left-center narrow path that isn't accessible via the center-bottom wide path. As such, it seems that narrow path could just be considered solid as far as the pathfinder was concerned. I realize that if the map has dynamic elements it might not be that simple, and I haven't thought through it beyond that simple observation, but it does bring to mind some sort of preprocessing and/or formation-specific metainformation.

Indeed, the map will certainly have dynamic elements, and an enemy in place will be treated the same as an obstacle. (I do treat members within a formation as passable to each other during pathfinding, though, to keep that from being chaos.) I did try some other approaches that involved doing the c_cost search beforehand and trying to get around using a heuristic (h_cost) function at all by instead reconstructing the path by following a trail of lowest c_cost values, but they all ended up being more expensive and/or less reliable than the current approach. This is something I will give some thought to, but another thing to consider is that this same function will be called in the middle of an already calculated route if the leader is blocked by something, namely another unit, along the way. Nothing jumps out at me immediately as pre-processable, but it is an angle I haven't given much thought.

But hey, solution or no, I appreciate you!

Thanks for the detailed response In a real-time context it seems like using multithreading and/or running the pathfinding algorithm iteratively might be of help, perhaps with cosmetic effects such as response animations or audio being used to help cover up the delay. I'll admit though I can't quite visualize how the 'step time' aspect works, and it may be that these ideas aren't applicable in that context. (And of course dynamic changes to the map could complicate both those approaches.)

Anyway, if you find yourself still looking for a solution, it might be useful to know exactly how the time spent on pathfinding impacts gameplay - in other words, in the context of 'step time', what it is exactly that gets delayed or slowed down by the pathfinding.

Just to be thorough, I'll also mention something you've probably already pursued, which is to profile if possible to see if there are any obvious remediable hot spots in your pathfinding implementation.

Multithreading is a thought I hadn't considered, if I break up the calculation of the path into parts. I was reading earlier about an approach that simultaneously approaches the destination from the start and the start from the destination and joins them where they meet. That is a serious candidate for a potential solution, thank you. Not sure entirely what you mean by running the algorithm iteratively though, could you explain?

Thanks for the video. The 'smart' formation movement is very impressive.

In a real-time context, by iterative I mean that you'd run some number of steps of the pathfinding algorithm each frame. That could be a fixed number of steps, or however many steps you could fit into an allotted time slice.

However, I still don't know whether multithreading or iteration will help here or not. The purpose of those techniques would be to allow other aspects of the game to proceed while the path is being computed. For example, in a real-time game, the units could respond, animate, mill around, etc. while the path was being computed, and all other aspects of the game (other units moving, interacting, etc.) could continue. But it may be that none of that is relevant in your case.

Can you identify where in the video the (presumed) pause or delay due to the pathfinding occurs? Is it after you issue the 'target' command and before the 'command' prompt returns? Or somewhere else?

Sorry if I'm being a bit dense about how the game works. The video is illustrative, but I'm still not entirely clear on how it all works in practice.

At the risk of asking a dumb question, is this the game itself - that is, is the game played in a terminal with a command prompt? Or is this just a testbed? (Sorry if you've already addressed that or if it seems like a ridiculous question - I'm just trying to get a clearer picture of what's going on exactly.)

Couple of ideas:

If you modify your test example to force classic A* to find the indicated correct route (by closing off all passages that are smaller than required), and run simple A* on it, is it faster? By how much? If it is, the problem should be your extra "obstacle finding" addition to A*. If it's not, the problem is your implementation.

If "classic" A* is much faster (e.g. order of magnitude or more):

1.  you could try running multiple A* searches with clearance, with gradually decreasing the required clearance (thus avoiding the problem of not finding any solution), or
2. running simple A* on multiple versions of the map (which you could get by processing your map with e.g. morphological erosion or something similar that gradually narrows "paths"). You could do the multiple maps in preprocessing, although you mentioned dynamic obstacles, which would mean you would need a clever way of updating multiple versions of the map. If you go the route of multiple searches, you can even do them in parallel.
3. you could generate a distance field on you map to have the path "gap" sizes available without searching locally at every node.

If "classic" A* is not much faster, then you have to optimize your code. Try measuring with a profiler. I'm not experienced enough in python to spot a performance problem just by looking at your code, but the usual suspect in algorithms like this is using containers suboptimally - wrong type of container, copying containers when it's not necessary, etc. You can also consider rewriting the pathfinding in C/C++ and calling it from your Python code.

Can you profile your code? I guess a lot of your time is going into the computation of `c(position)' (a better name for that function would be nice, by the way). Perhaps you could memoize that function, or just pre-compute its value for the whole map? You can probably pre-compute the value of the function in every location much faster than calling the function at every location. Also, in your implementation of `clear_area', you could pass in the value of `optimal_area', so you can stop looking at larger and larger rings around the position when you really don't care what the exact result is.

5 hours ago, Andor Patho said:

you could generate a distance field on you map to have the path "gap" sizes available without searching locally at every node.

I had a similar idea:

For each cell, calculate how open it is (trivially by counting how much blocked cells are in a 5x5 neighbourhood, or using some smarter method like obstacle distance field). Then use this openness as weights (or cost) for the traditional A* algorithm. 

Woudn't the leader then follow paths with low amount of surrounding obstacles, avoiding all the complexities, but ensuring the entire group has enough space to keep the formation most of the time?

In your original example, the formation doesn't fit through the gaps: for instance, 4 and then 2 hit a X on their right as V enters the gap as drawn in the third figure. What are the exact constrains your formation need to obey? How large can they be?

Since the map appears to be quite static, you could precompute pathfinding graphs for different formation shapes (i.e. the leader can walk into an adjacent walkable cell only if the other formation members can walk into the respective offset cells). It would be easy, exact, and cheap unless you have too many formation types for your memory budget or really huge maps.