Hello dear graphics folk,

 I have a game that uses tiles of (flat-topped) hexagons. I want the hexagon to be separated into six triangles (n=0), and those triangles separated into another six*four = 24 (n=1) triangles, and so on...

I (hypthetically) need the vertices of various depth for height-mapping (n=3), but also for pathfinding purposes(n=4) and structure placement(n=2). (See attached reference)

I am using the Unity3d Mesh class and managed to create the hexagon with this page on hexagons.

What I need is an algorithm that can tessellate the hexagon into triangles with depth n. I do not want to dublicate vertices (except where two hexagons meet, for simplicity). There seems to exist a button in Blender, which does exactly what I need. But I want to do it myself on runtime to use Perlin Noise (or similar) for height.

Is there already such an algorithm? Do you recommend some resource? Maybe I am missing the right term to google it properly?

To be more accurate: How do I find, count and order the vertices in a smart way, that makes constructing the triangles as elegant as possible?

If you had a pregenerated hex mesh, its just dividing triangles into 4 smaller ones. Stitching means being aware of neighbours and their level. That mesh class you linked is pretty stupid, not in an insulting way but I mean it is not aware of its neighbours so how will you deal with stitching different levels together? Also how do you know if you already made a new vertice for a subdivision and what is its index? A triangle in that link is just 3 indices to vertices, so I would add more verts for the smaller triangles and then be able to find them. I would probably add an additional field to the triangle class to index its children and mid point vertices and neighbours:

Struct Triangle // or class whatev's

{

int[3] corners; // indices to the array of vertices for the corners

int[3] midpoints; // these would be -1 if not made yet, and indices if they are

int[4] childTris; // indices to the triangles array -1 for no children or an index if the child has been made

}

Also maybe an int pointing to the parent to make walking the whole thing easier, and if you are displaying levels based on LOD (not sure that seemed like a requirement) some kind of value to help the GPU know what level to render (like the mid point position of the parent and then you could render the level based on distance from camera). I'm confident that would also be adequate for stitching on a height map.

I do almost exactly this and it's actually quite simple, but......I use a data structure with explicit edges, which are shared by neighboring triangles. trangles are stored in a quadtree. So each tri can have four children. The edges are in a binary tree, and so each edge has two children. Then the whole thing is simple. When you ask an edge for its midpoint and child edges, if it needs to, it subdivides, otherwise it just returns the data it already has, because its neighbor has asked already. BTW, this is the perfect place to implement some sort of reference counting, but there are a few details. The edge trees should have weak back pointers and the edge child pointers should also be weak.  When an edge is deleted, it deletes it's reference in its parent. Strong pointers are from parent faces to child faces and also from faces to edges and from edges to vertexes. Now when a parent face deletes its children, everything else that needs to be deleted, is deleted automatically.

the number of unique vertices per triangle per level of subdivision (not per hex) should be integer sequence https://oeis.org/A028401

btw: if all triangles are supposed to have the same depth of subdivision, don't use pointers - just use a flat array and calculate indices.

Hello, and thank you for your support!

On 10/18/2018 at 11:14 AM, TeaTreeTim said:

That mesh class you linked is pretty stupid

Yes, I linked it to show what I have available, so basically nothing. It also shows what I need to feed to the class to make a mesh appear. What I need is to fill the Mesh.vertices[] and the Mesh.triangles[].

To make my questions more precise: (They mainly revolve arround the structure/architecture of data storage)

1. In what fashion do I index the vertices? Is there some "best practice" amongst graphic programmers?

2. Is there a fitting, elegant algorithm already existing that matches the indices of the vertices[]-array to the triangles[]-array?

3. (Partly answered) How do I store the information for later usage in the pathfinder?

This is what I got so far (creating a flat hexagon in C#):

using UnityEngine;

public class D_HexTile : MonoBehaviour
{
    public float mSize = 1f;
    public Material mMaterial;

	void CreateHex()
    {
        gameObject.AddComponent<MeshFilter>();
        gameObject.AddComponent<MeshRenderer>();
        Mesh mesh = GetComponent<MeshFilter>().mesh;

        mesh.Clear();

        // === Vertices ===
        Vector3[] vertices = new Vector3[7];
        vertices[0] = transform.position;
        for(int i = 1; i < vertices.Length; i++)
        {
            vertices[i] = GetCorner(transform.position, mSize, i - 1);
        }
        mesh.vertices = vertices;

        // === Triangles ===
        int[] triangles = new int[6 * 3];
        int triNum = 1;
        for(int l = 0; l < triangles.Length; l++)
        {
            if (l % 3 == 0)
            {
                triangles[l] = 0;
            }
            else if(l % 3 == 1)
            {
                triangles[l] = 1 + (triNum % 6);
            }
            else if(l % 3 == 2)
            {
                triangles[l] = triNum;
                triNum++;
            }
        }

        mesh.vertices = vertices;
        mesh.triangles = triangles;
	}

    private Vector3 GetCorner(Vector3 center, float size, int i)
    {
        float angleDeg = 60f * i;
        float angleRad = Mathf.Deg2Rad * angleDeg;
        return new Vector3(center.x + size * Mathf.Cos(angleRad),
                           center.y,
                           center.z + size * Mathf.Sin(angleRad));
    }
}

I omitted parts for UV's and normals. I show this to give an example usage of the Mesh-class ... Now I have to feed it.

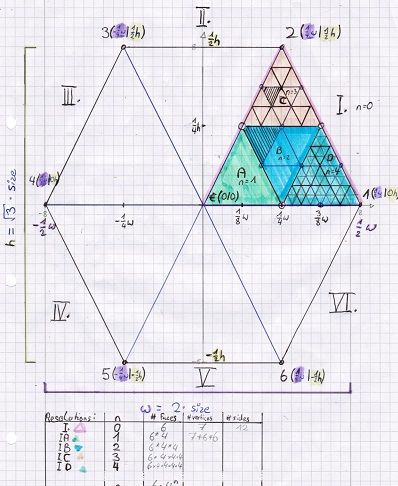
So, this is obviously not enough. GetCorners() will suffice for the hexagon corners, but using the midpoints by doing vector-math for sub-devided triangles (as you suggested) seems more appropriate. So, now I have to deal with the questions above.

I can't seem to wrap my mind arround what question to prioritize first. The answer to question 2. depends on how I deal with 1. and 3.

If I want the indices stored in a certain way, I will have to traverse the QuadTree / BinaryTree in a certain way (whatever that will look like).

The other way arround: When I store the sub-devided triangles in a certain way, they may predefine the indices of the vertices.

On 10/18/2018 at 12:08 PM, Gnollrunner said:

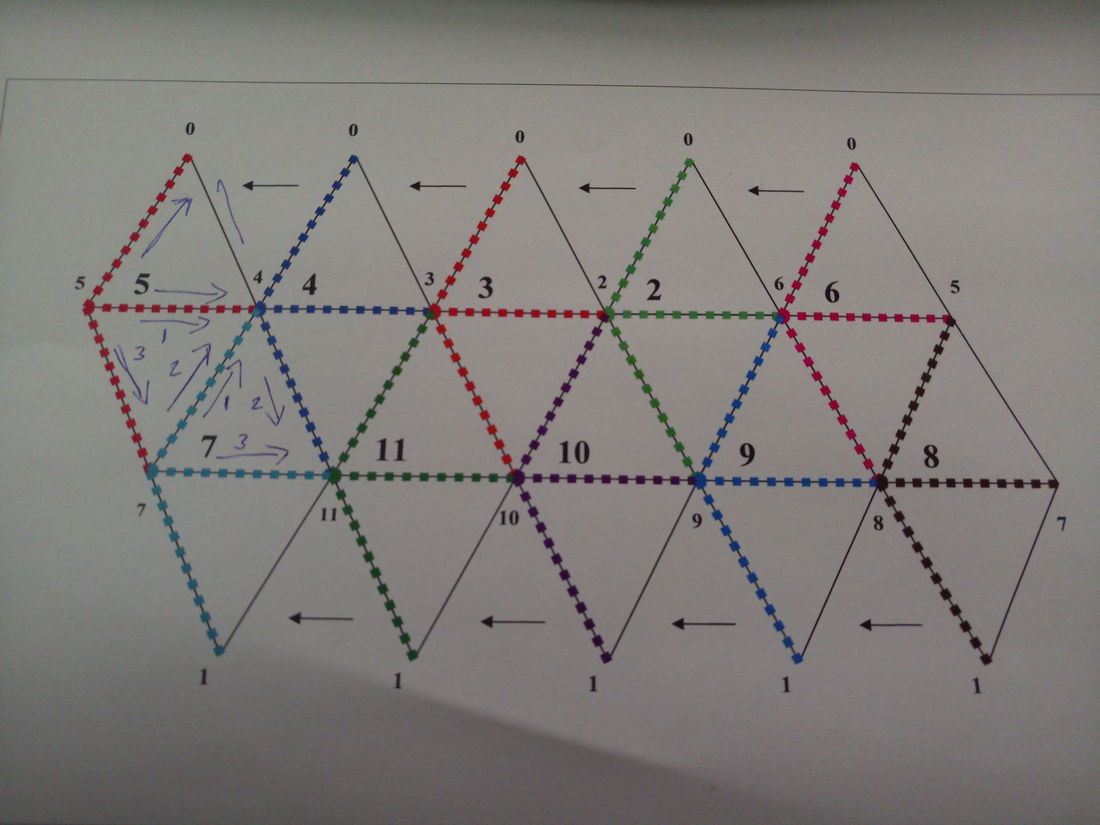
I use a data structure with explicit edges, which are shared by neighboring triangles. trangles are stored in a quadtree.

 I found this idea very inspiring and would like to know more. I will probably need the edges more often than the faces (pathfinding).

Do I understand this correctly, when I say the following?

 I have a List of edges. When it is just the hexagon, I have 12 of them. 6 of those contain data for two triangles, the other 6 have only one triangle (the outer edges). I thereby have 3 references to any one triangle. When I call SubdevideTri() on any triangle, it will tell all three edges to SubdevideEdge() and then .... .... well, this is where my brain locks up ....

To the point: @Gnollrunner Could you ellaborate on how you did this?

How is your data stored? Do the edges contain the corners and the triangles? Why do I need the triangles stored in a QuadTree, when I already have their reference in the edges, stored in 6 BinaryTrees? What about the new edges "in between" midpoints?

Or is the QuadTree of triangles the "dominant" storage? Do the triangles reference the edges? Do I really need the BinaryTree in that case?

Or do you do both, to simplify access?

I will try things out a bit and come back to you.

On 10/18/2018 at 5:29 PM, ninnghazad said:

the number of unique vertices per triangle per level of subdivision (not per hex) should be integer sequence https://oeis.org/A028401

Valueable knowledge, thank you for this!

Thanks again for your support! Cheers!

2 hours ago, Rockroot said:

 

To the point: @Gnollrunner Could you ellaborate on how you did this?

How is your data stored? Do the edges contain the corners and the triangles? Why do I need the triangles stored in a QuadTree, when I already have their reference in the edges, stored in 6 BinaryTrees? What about the new edges "in between" midpoints?

Or is the QuadTree of triangles the "dominant" storage? Do the triangles reference the edges? Do I really need the BinaryTree in that case?

Or do you do both, to simplify access?

I will try things out a bit and come back to you.

Ok where to begin.... First off I just noticed you were using Unity which means you are probably using C#.  I haven't used C# in a long time an in general I don't like managed languages for algorithmic work, because I feel it handcuffs you somewhat in how you build your data structures.  I guess you sill have some sort of weak pointers in C#, but I'm not exactly sure how they work. However maybe you can do something similar to what I did in C++.

So just to reiterate. We have vertexes, edges, and faces (triangles) .  You are starting with hexes so you could also do a top level hex class if you want with six sub faces which gets you to your tri-faces. Or you could just do all tri-faces and flag the internal edges as special. It really depends on the details of what you want to do.

In any case once you get to the tri-faces, each tri-face references  3 edges and each edge references two vertexes. so there's the basic structure.  Now you want to subdivide tri-faces to n levels. Each tri-face needs to be able to reference 4 child faces.  Three will have the same orientation, and the center one (I call face 4)  will be upside down. Likewise each edge needs to be able to reference 2 child edges. Edges are naturally directed meaning there is a vertex #1 and a vertex #2.  What I do is I keep 3 bits in the tri-face that describe the orientation of each edge relative to it's face. This way it's easy to go clockwise or counterclockwise around your face. Remember an edges will have the opposite orientation for the face on the other side of it. You can also add a 2 slot array of weak pointers from edges back to faces and you can index that with your bit codes or rather the inverse ( ! ) of your bit code to get to the opposite tri-face. That will let you do your path-finding quickly. It's also useful for going around a vertex and calculating mesh normals (although there is a faster way to do this depending on your specific needs)

Again when you need to subdivide a singe tri-face, just ask the edge to return it's two child edges. If it doesn't have any it creates them at that time. Now you have six edges (2 from each face) but you still need an additional 3 crossing edges for the center, which you can simply create from the appropriate end points of the 6 child edges you received. Once you have all 9 edges you can now build your 4 child faces and and add them as children to the parent. Each of those new faces can be subdivided in the same way and they will share edges and vertexes correctly. 

As for lists and stuff like that, I don't use any. You don't really need them except maybe for the very top level face geometry.  In certain cases having a vertex list might be useful, but if you are using this for LOD you will be creating and destroying vertexes, edges and faces in semi-random order and a list will just get in your way. I just ended up doing a post processing step that walks the whole faces tree, visits nodes and assigns indexes to the nodes. It also simultaneously writes them to the graphics card.  You just need a flag bit on the vertex to make sure you don't write a vertex more than once.  If you aren't using this for LOD your requirements are a bit simpler and you might want to use a vertex list in that case.

This is a place where the exact implementation will likely be different from C++ to C#. In C++ you will typically have a custom heap and might use reference counting.  In C#.... well.... someone with more C# experience will be able to better help you. You also have the option of writing most of this code in C++, and then linking it into C#.

Another issue you will have if you are building meshes this way is cracks. You can even see where you will have them in the picture in your first post. There are a couple ways to handle this.  First I want to say I recommend not having more than one level of difference between neighboring triangles.  There are two reasons for this.  First to fix the cracks you might need to have some special triangles subdivisions . Here's a little drawing I made when I did mine:

Notice you don't have more than 3 sub-faces so you can store those in your child-face fields without modifying your data structure.  if you have one faces next to a highly sub-divided neighbor you will need a more complex crack healing strategy. Most likely you will put a point in the middle then put radials out to the edge vertexes.  At big levels of difference this looks crappy, especially with noise based stuff. In order for this to be useful you have to sub-divide based on some error between the noise function and the new nodes you want to add. However I tried this, and I found the function would quite often fool the algorithm. The edge points would look like they were close to the function but the center could vary quite quite a bit. In short it just looked crappy in places. Having one level of of mesh difference ended up being way better and simpler to boot. You just base it on the square of the distance to the viewer. Again I'm assuming you're doing LOD here.

A few more points .... I talked about edge direction above. If you terrain is flat you might be able to get a way with a standard edge direction. I'm doing a sphere so there is a minor difference in the way I handle it. In any case my standard is as such:  Edge 1 goes clockwise, Edge 3 goes counter clockwise and Edge 2 can go either way.  I label my tri-faces as as either Point Up or Point Down. If your terrain is flat then Edge 2 of all Point Up faces will be clockwise, and counter clockwise for all Point Down faces. This next picture is a flattened icosahedron.  Just ignore the colors and numbers for a second. Those are for a special coordinates system for trees and rocks, etc.  Look at the left where I drew in some stuff for you. The bottom red tri-faces is Point Down, The the upper teal tri-face is Point Up.  Note the directions and the edge numbers. Even though this standard works, you still might want to keep the bit codes to handle the special crack healing faces. If you are doing this on a sphere like me, you need to support both directions of Edge 2 to handle the low and high latitudes of the world, but the rest is the same.  Also this is just my standard. It's not some common thing. You can use whatever standard you like for this.

So I guess that's about it for now. It might sound a bit complex but I implemented the system in about a day minus the crack healing code. This was the second time around. First time it took me quite a while to figure it all out but once you know the tricks it's not that bad.