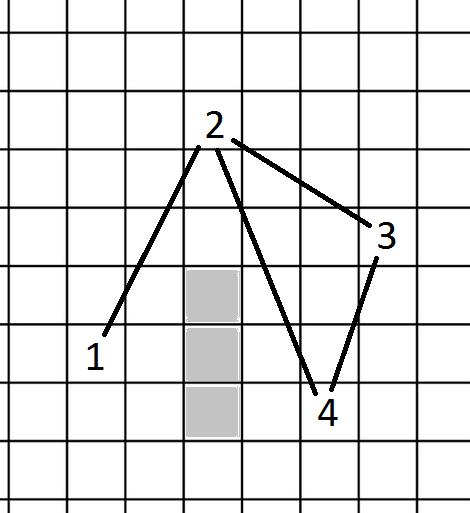
Im using micropather, a c++ implementation of a* pathfinding in my games. I got it to work fine with a strict grid-based system, but now need it to also work with "nodes". My setup is like this:

1. I have a collection of nodes. Each node has a X/Y-position, an ID, and an array of max 10 node-ids it can move to ("adjacent nodes").
2. Which nodes are reachable from each node are checked (based on a max distance and not having any obstacles between them).
3. Cost to move from a node to another is simply the distance between the 2 nodes' positions.

I guess some things will be silimar to how a grid works, but im not sure how to reconstruct the code.

It's the exact same, so you'd have to give more details as to your specific case.

If you work with pathfinding, using nodes is always the general case, a grid is a possible optimization / specific case which can improve parts of the algorithm using assumptions about the structure.

Try to outline which parts you're having trouble with, all concepts should have a 1 : 1 mapping between grids and nodes.

I guess its the "find adjacent" and "adjacent costs" i need to fix. (i dont have it in front of me right now:). More info will follow! But in the grid version i just give the pather the pointer to the start of the 2D-array holding map data (terrain type for each tile) so now maybe a pointer to the array of all the nodes?

I assume it's best to calculate the adjacentCost (cost/distance from a node to each of its linked nodes) beforehand and store them (in each node). Otherwise I need to calculated such distances thousands of times each pathfind. When it was a grid i just used the adjacentCost of "1" (or 1.41 for diagonal movement) so no calculation was needed.

So something like:
 

class pathfindingNode{
  int id;
  int posX, posY;
  int adjacent[MAX_ADJACENT]; //the adjacent nodes(IDs) possible to move to. id -1 means no node at that slot
  float adjacentCost[MAX_ADJACENT]; //cost to move to an adjacent node
};

Be careful with what you described. The only reason the A* optimization works is because of the geographic spatial format of the map matches the heuristic function. The heuristic provides a sort, allowing the first match to be the best match.  The more the nodes drift away from the actual map distances, the more the optimization breaks down.

With a regular grid where cells represent motions exactly, A* works great because the heuristic is ideal. You can always estimate the amount left to reach the target by using the map distance.  With nodes representing areas, the heuristic is more difficult because it no longer perfectly represents the sorting criteria. 

When the heuristic breaks down so it no longer represents the approximate best remaining solution, then you need to revert back to plain old Dijkstra's shortest pairwise path algorithm. 

@Frob: not sure if I understand the problem, or if this would be a problem for me.

After code inspection: So much of my code (both finding and storing the path and following it) depends on a grid (and I need one anyway for drawing the world / placing objects) I now consider this setup:

1. Use my tried and tested grid-based A* system.
2. Add a "node-based mode". This is work the same way but also keep track of the "nodes" in the way described above. Basically they inform the pather which are the adjacent "tiles" to each node-tile. So when running the grid-mode each tile has 8 adjacent tiles, but when running the node-mode it will check the structure outlined above for which (up to) 10 adjacent tiles are reachable from that tile.

So basically I would pathfind over a restricted grid where only certain tile-to-tile connections are allowed.

Seems doable?

It's not clear what the problem is here, since 99% of A* implementations are "pathfind over a restricted grid".

It's also not clear how you have a grid but also seem to have up to 10 neighbours, but if your heuristic is guaranteed to be an underestimate, your path length guaranteed to grow monotonically with each node, and each node represents a distinct state, then you should have no problems, no matter how many neighbours each node has.

I  propose to use the grid as normal (a 2d array of tiles), but I also give the pather access to my collection of "nodes". These have (max )10 neighbours which make up the "restriction".

So when a tile checks for "neibours", they used to find all 8 adjacent tiles, but now it looks in the node-collection which tiles it could add as possible neibours. See the pic below. Node 3 would have only node 2 and 4 as neibours for example. It cannot find the tiles "right next to it" as it would in my normal grid-based mode.

The nodes acts as my old tiles in other part of the code, they still have a x/y position which actually describes their position on the grid.

That should 'just work'.  I mean, you have to be careful with any assumptions you're doing with your pathfinding code with regards to the adjacent nodes, but other than that, it should just work.  This is basically how one would implement teleporters, elevators,  jumppads or other shortcuts.

Yay it works!

@Frob Maybe i ran into the problem you mensioned though:
It always finds a path, but in certain circumstances it chooses a valid path that are slightly longer (around 10 %) compared to the most optimal path. I use distance (float) between nodes as movement cost for that connection. If I move that node so that path is now 20-30 % longer it will choose the shortest path instead. Any idea where this slight error may come from?

Yes, that is exactly the issue described above.

Repeating, A* is an optimization based on certain guarantees and requirements.  When you start relaxing the guarantees (such as a range of values rather than a single value) then the quality of your results also relaxes.  The more you relax the rules the worse the results become. You can try to mitigate it such as using the worst point in the range since you no longer have an exact point, but nothing will correct the fundamental issue that you're violating the algorithm's requirements.

It gets back to the simple rules of computer science. Algorithms come with certain requirements. If you cannot meet those requirements then you cannot use the optimizations.  Fundamentally A* is Dijkstra's pairwise shortest path algorithm with some optimizations when requirements are met; break the requirements and you lose the optimizations and need to do the full search.

If you can start to restore those requirements through understating values, you can start to restore the quality of the results.