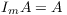In that case, mathematically is subscript Mij always interpreted as the i-th column and j-th row of Matrix M?
Regardless of the major of the matrix?
Rows and columns only exist in your mind.
They don't exist in math, they don't exist in computers (not entirely true, but for now, assume it).
We like to structure information, so we invented rows and columns, as it helps us think in higher level structures. If you look careful though, you'll see they don't really exist. (Or rather, you can choose to ignore them, and everything still works.)
An author may say Mij is a matrix, and then picks either i or j as row. That is however just the author creating structure for us. (Mathematicians tend to use the first index as row, computer scientists tend to take the first index as column, I guess we are more horizontally oriented  )
)
While the author may use words like row or column, in the math "code" itself however, there is no row or column, just M and 2 indices. Its meaning is that for every unique combination of i and j, you have a unique value Mij. It doesn't matter if you see columns, rows, separate variables, or whatever. Each unique combination of i and j gives a unique Mij, that is all it says.
It means that M11, M12, M21, and M22 are all different values. It's like
int p1, p2, p3, p4;
in your mind, you may see "p" here as a row or a column, but it's just 4 different variables, conveniently numbered, as I am too lazy to write
int loop, bar, catchy, fred;
there is no row, just 4 variables, written by a lazy programmer.
On to computer systems.
If you use a programming language other than assembly language for programming, chances are that it supports multi-dimensional arrays in some form, eg "int foo[5][6];". The same as above holds here. The compiler handles memory allocation for you. It also handles making sure that "foo[1][2]" gives you a unique value different from all values "foo[x][y] where x != 1 or y != 2". You can see "foo" like the "M" variable in math, just a lot of unique variables, conveniently numbered to save you the effort of inventing unique names for them.
You are free to interpret "foo" as just 30 separate variables, as 5 rows and 6 columns, as 6 rows of 5 columns, as an array of arrays holding 6 integers, and many other interpretations. As long as you keep in mind foo[a] == foo[x][y] if a==x and b==y, any interpretation you want to have works.
So where does row-major and column-major comes in then?
The problem in computers is that memory is not paper. Computer memory is completely linear, first byte is at address 0, last byte around address 340282366920938463463374607431768211455 (for a 32 bit system). In other words, memory is one VERY long row in memory (like "byte mem[340282366920938463463374607431768211456]"). As a result, only 1-dimensional arrays actually exist
, like
int bar[30]
The question is now how to fit "foo[5][6]" onto that array? The compiler just made us believe "foo[5][6]" exists.
There are 2 common solutions in use: foo[j] == bar[i + j*5] or foo[j] == bar[j + i*6]. This is what the compiler of your programming language is actually doing. You write foo[j], and the compiler then translates that to access in the "bar[x]" array.
As you can see, while you can interpret rows and columns in "foo", they actually don't exist. It's all flattened to one long linear array, since that's the only way the computer allows storage.
Now, by convention, my first solution is called column-major, and my second solution is called row-major. The reason is that mathematicians made the first computers, and thus saw "i" as "row" in their mind. "major" just means "when you increment this index, you make a big jump in memory".
"row-major" thus means "make a big jump in memory if the first index changes".
While sometimes you may want to care about the above foo -> bar mapping done by the compiler (see below), but you can also choose to ignore it. Everything will still work.
And there you have the entire story. Bottom line is
1. you can think in rows and columns as you want, as long as you do it consistently. Any interpretation will work (including my idea that rows and columns only exist in your mind), as long as you use the same interpretation consistently.
2. Secondly, row-major and column-major is completely irrelevant, until
- You want to implement multi-dimensional arrays in your compiler
- You want to use the "bar[30]" interpretation at the same time as the "foo[5][6]" interpretation (eg when loading data from a file)
- You are in a hurry, and want to control when you make big jumps in memory.
Footnote:
Actually, an "int" is bigger than a byte, so bar[0] needs more than one memory address. The foo -> bar mapping is thus foo[j] uses memory[base_of_bar + (i + j*5)*4] to memory[... + 3].