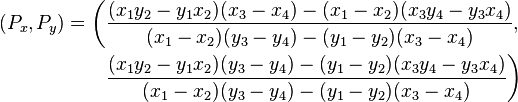Hello.

I have this image first:

Notice:

1:Triangle

2:Rectangle

3:Two green dots

How do i find the two green dots position if objects exist in 2d space?

What i have is a triangle that at one point will be colliding with rectangle and i need to remove the part of the triangle that is colliding with rectangle, to do such i thought about making few triangles from the existing triangles.

I need to end up with following triangles.

The issue is i do not know how to get the green positions on the rectangle if someone would be kind to provide any kind of help or hints i would be glad i do not know from where to start.

Edit::
I made a example to show what i need calculated

I want to write function as:

void Generate_Intersetion_Points(sf::Vector4i rec, sf::Vector2i line, std::Vector<sf::Vector2i> & generatedPointsPosition);

The function would take rectangle and a line and feed intersection point intro the vector, the issue is i don't know the math required, some hints would be great to start with.

Have you tried testing the rectangle against the three separated lines or some other simplified approach?

Have you tried testing the rectangle against the three separated lines or some other simplified approach?

I do not understand what you mean by "the three separated lines" and i do not know other simplified approach.

By looking at images i understand its about two lines intersecting and finding where, wasn't able to find math for that calculation yet.

Edit::
Ok i understand what you wanted me to do, but i do not see how to get the results i need.

Also i feel this is simplified so much from the original problem i am facing.

Putting words into dejaime's mouth/hands:

A triangle has 3 lines.

You can split the "Triangle vs Box" intersection problem into 3x "Line Segment vs Box" intersection problems, 1 per line of the triangle.

There might be more efficient ways of doing it, but it should give you a starting point.

I haven't used this reference personally, but it might be of some assistance:

http://www.3dkingdoms.com/weekly/weekly.php?a=3

It looks like you are underestimating, both, the problem and the proposed simplification.
Testing a rectangle against a line to get the intersection points is easier, it may have zero, one (in case it hits a corner), two intersection points or several (if the line is perfectly over one of the rectangle's sides).
You'll find it with google in no time.

But the rectangle against a triangle is substantially harder.
You can have zero intersections, a single intersection point (one corner on another corner or on a line).
You can also have two points, when one corner of one shape is inside the other, as in your picture.
But there is a problem here, you can have two intersection points if an entire side is inside the other shape, as in here:


Notice it has two intersection points, but on two different sides of the rectangle.

It may also have three points (two line vs line and one "corner vs line"), four (all line vs line), and more...

Sorry for the blur, I had to resize it.

If you break down the triangle in different lines, it will be easier to check how many intersections there are, and how exactly these shapes intersect...

If this is in 2D space, the math can be a bit challenging. I solved this a few years ago by digging up some musty old grade school algebra books. The general principle here is to think of your shapes as a collection of lines, or a collection of vertex points. A triangle has three vertices, a rectangle has four, a pentagon has five, etc. What we want to note is that the number of sides/vertices in a shape shouldn't really matter very much. To detect if any two shapes overlap, or intersect, we can test each line in the first shape against every line in the second shape. If no lines in the first shape intersect with lines in the second shape, then we might not have a collision (note: A shape could still be completely enclosed within another shape!).

How do we do this?

Well, we have to define a "line". Algebraically, it would be defined as "Y = mx + b", but that's a general line formula which stretches on to infinity. For the sides of a shape, you want to define a line by a starting point and an ending point. Then, you want to do a line intersection test against every other line in the other shape (We're looking at an N^2 for loop here... watch out!)

Anyways, the code I came up with is here:

/// <summary>
/// Given the end points for two line segments, this will tell you if those two line segments intersect each other.
/// </summary>
/// <param name="A1">First endpoint for Line A</param>
/// <param name="A2">Second endpoint for Line A</param>
/// <param name="B1">First endpoint for Line B</param>
/// <param name="B2">Second endpoint for line B</param>
/// <returns>true or false depending on if they intersect.</returns>
public static bool DoIntersect(Vector2 A1, Vector2 A2, Vector2 B1, Vector2 B2)
{

	//NOTE: Floating point precision errors can cause bugs here. This can result in false-positives or true-negatives.

	//Based off of the Y = mx + b formula for two lines.

	//calculate the slopes for Line A and Line B
	double mx1 = (double)(A2.Y - A1.Y) / (double)(A2.X - A1.X);
	double mx2 = (double)(B2.Y - B1.Y) / (double)(B2.X - B1.X);  

	//calculate the y-intercepts for Line A and Line B
	double b1 = (double)(-mx1 * A2.X) + A2.Y;
	double b2 = (double)(-mx2 * B2.X) + B2.Y;

	//calculate the point of intercept for Line A and Line B
	double x = (b2 - b1) / (mx1 - mx2);
	double y = mx1 * x + b1;

	if (double.IsInfinity(mx1) && double.IsInfinity(mx2))
	{
		//we're dealing with two vertical lines. If both lines share an X value, then we just have to compare
		//y values to see if they intersect.
		return (A1.X == B1.X) && ((B1.Y <= A1.Y && A1.Y <= B2.Y) || (B1.Y <= A2.Y && A2.Y <= B2.Y));
	}
	else if (double.IsInfinity(mx1) && !double.IsInfinity(mx2))
	{
		//Line A is a vertical line but Line B is not.
		x = A1.X;
		y = mx2 * x + b2;

		return (
			((A1.Y <= A2.Y && LTE(A1.Y , y) && GTE(A2.Y, y)) || (A1.Y >= A2.Y && GTE(A1.Y, y) && LTE(A2.Y, y))) &&
			((B1.X <= B2.X && LTE(B1.X, x) && GTE(B2.X, x)) || (B1.X >= B2.X && GTE(B1.X, x) && LTE(B2.X, x))) &&
			((B1.Y <= B2.Y && LTE(B1.Y, y) && GTE(B2.Y, y)) || (B1.Y >= B2.Y && GTE(B1.Y, y) && LTE(B2.Y, y))));
	}
	else if (double.IsInfinity(mx2) && !double.IsInfinity(mx1))
	{
		//Line B is a vertical line but line A is not.
		x = B1.X;
		y = mx1 * x + b1;

		return (
		((A1.X <= A2.X && LTE(A1.X, x) && GTE(A2.X, x)) || (A1.X >= A2.X && GTE(A1.X, x) && LTE(A2.X, x))) &&
		((A1.Y <= A2.Y && LTE(A1.Y, y) && GTE(A2.Y, y)) || (A1.Y >= A2.Y && GTE(A1.Y, y) && LTE(A2.Y, y))) &&
		((B1.Y <= B2.Y && LTE(B1.Y, y) && GTE(B2.Y, y)) || (B1.Y >= B2.Y && GTE(B1.Y, y) && LTE(B2.Y, y))));
	}

	//figure out if the point of interception is between all the given points
	return (
		((A1.X <= A2.X && LTE(A1.X, x) && GTE(A2.X, x)) || (A1.X >= A2.X && GTE(A1.X, x) && LTE(A2.X, x))) &&
		((A1.Y <= A2.Y && LTE(A1.Y, y) && GTE(A2.Y, y)) || (A1.Y >= A2.Y && GTE(A1.Y, y) && LTE(A2.Y, y))) &&
		((B1.X <= B2.X && LTE(B1.X, x) && GTE(B2.X, x)) || (B1.X >= B2.X && GTE(B1.X, x) && LTE(B2.X, x))) &&
		((B1.Y <= B2.Y && LTE(B1.Y, y) && GTE(B2.Y, y)) || (B1.Y >= B2.Y && GTE(B1.Y, y) && LTE(B2.Y, y))));
}

/// <summary>
/// Equal-Equal: Tells you if two doubles are equivalent even with floating point precision errors
/// </summary>
/// <param name="Val1">First double value</param>
/// <param name="Val2">Second double value</param>
/// <returns>true if they are within 0.000001 of each other, false otherwise.</returns>
public static bool EE(double Val1, double Val2)
{
return (System.Math.Abs(Val1 - Val2) < 0.000001f);
}

/// <summary>
/// Equal-Equal: Tells you if two doubles are equivalent even with floating point precision errors
/// </summary>
/// <param name="Val1">First double value</param>
/// <param name="Val2">Second double value</param>
/// <param name="Epsilon">The delta value the two doubles need to be within to be considered equal</param>
/// <returns>true if they are within the epsilon value of each other, false otherwise.</returns>
public static bool EE(double Val1, double Val2, double Epsilon)
{
return (System.Math.Abs(Val1 - Val2) < Epsilon);
}

/// <summary>
/// Less Than or Equal: Tells you if the left value is less than or equal to the right value
/// with floating point precision error taken into account.
/// </summary>
/// <param name="leftVal">The value on the left side of comparison operator</param>
/// <param name="rightVal">The value on the right side of comparison operator</param>
/// <returns>True if the left value and right value are within 0.000001 of each other, or if leftVal is less than rightVal</returns>
public static bool LTE(double leftVal, double rightVal)
{
return (EE(leftVal, rightVal) || leftVal < rightVal);

}

/// <summary>
/// Greather Than or Equal: Tells you if the left value is greater than or equal to the right value
/// with floating point precision error taken into account.
/// </summary>
/// <param name="leftVal">The value on the left side of comparison operator</param>
/// <param name="rightVal">The value on the right side of comparison operator</param>
/// <returns>True if the left value and right value are within 0.000001 of each other, or if leftVal is greater than rightVal</returns>
public static bool GTE(double leftVal, double rightVal)
{
return (EE(leftVal, rightVal) || leftVal > rightVal);
}

It could probably be improved by someone smarter than me, but it works well enough for the time being. Note that math like this is susceptible to floating point precision errors so I had to write my own floating point comparison "==" methods with a small epsilon value. I'm still not 100% confident this is perfectly bug free.

Also, since the method I suggest above uses an N^2 approach, you might want to consider using a broad-phase and narrow-phase collision check (if you notice performance problems!). The broad phase check could just be sphere vs sphere intersections, where each sphere completely encloses a shape. It's very fast to implement and doesn't cost much. If the spheres intersect, then you can run the N^2 check for more precision.

There's one other thing you might want to consider: If you're just trying to use one shape to overlap another shape, why don't you just toggle the drawing order of the shapes? Is there a game logic reason behind it?

Thank you all on helping me resolve the issue.

Pretty much self explanatory, If anyone will ever search for here it is, i hope images don't get deleted any time soon

void PrintIntersectionOfTwoLines(sf::Vector2f & one, sf::Vector2f & two, sf::Vector2f & three, sf::Vector2f & four)
{
//To not calculate it two times
    int calcFirst = (one.x*two.y)-(one.y*two.x);
    int calcSecond = (three.x-four.x);
    int calcThird = (one.x-two.x);
    int calcFourth = (three.x*four.y)-(three.y*four.x);
    int calcFifth = (three.y-four.y);
    int calcSixth = (one.y-two.y);

//x is the intersection point on x axis
    int x = (calcFirst * calcSecond - calcThird * calcFourth) / (calcThird * calcFifth - calcSixth * calcSecond);
    std::cout<<"X:"<<x<<std::endl;
//y is the intersection point on y axis
    int y = (calcFirst * calcFifth - calcSixth * calcFourth) / (calcThird * calcFifth - calcSixth * calcSecond);
    std::cout<<"Y:"<<y<<std::endl;
}

The function if anyone needs it.

EDIT:: i will probably post how i divided my rectangles in future if i don't forget.

The code looks a lot more simple than mine, so I tested your code to see if it worked -- and I found a few problems!

First problem: You're using integers to store the results of mathematical operations on floating point numbers. This gives you wrong math. So, I went ahead and changed those..

Second problem: If you try the two line segments (-1,0)->(1,0) and (20,1) -> (20, -1) and run the code, you should expect there to not be any intersections. Yet, the results show an intersection at (20,0), which is totally wrong.

Potential problems:

-If two lines are the same, you get infinity results. If you're only expecting one X and Y value, this could be problematic.

-If two lines are parallel, you get infinity and NaN results (you're dividing by zero). This could also be problematic if you're not testing for them.

Here's my test code:

class Program
{
	static void Main(string[] args)
	{
		int a = (int)(1.1f + 1.2f);//<-- see? you lose precision and get wrong values.
		Console.Write(a);
		//PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(2, 1), new Vector2(2, -1));  //good
		//PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(2, 1), new Vector2(2, -1));  //good
		//PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(2, 1), new Vector2(2, -1));  //wrong
		//PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(-1, 1), new Vector2(1, 1));    //parallel: funky values
		//PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(-1, 0), new Vector2(1, 0));    //same line: wrong
		PrintIntersectionOfTwoLines(new Vector2(-1, 0), new Vector2(1, 0), new Vector2(20, 1), new Vector2(20, -1));  //wrong
	}

	static void PrintIntersectionOfTwoLines(Vector2 one, Vector2 two, Vector2 three, Vector2 four)
	{
	//To not calculate it two times
		float calcFirst = (one.X*two.Y)-(one.Y*two.X);
		float calcSecond = (three.X-four.X);
		float calcThird = (one.X-two.X);
		float calcFourth = (three.X*four.Y)-(three.Y*four.X);
		float calcFifth = (three.Y-four.Y);
		float calcSixth = (one.Y-two.Y);

	//x is the intersection point on x axis
		float x = (calcFirst * calcSecond - calcThird * calcFourth) / (calcThird * calcFifth - calcSixth * calcSecond);

	//y is the intersection point on y axis
		float y = (calcFirst * calcFifth - calcSixth * calcFourth) / (calcThird * calcFifth - calcSixth * calcSecond);

		Console.Write("X: " + x + "\nY: " + y);
	}
}

The code looks a lot more simple than mine, so I tested your code to see if it worked -- and I found a few problems!

First problem: You're using integers to store the results of mathematical operations on floating point numbers. This gives you wrong math. So, I went ahead and changed those..

Second problem: If you try the two line segments (-1,0)->(1,0) and (20,1) -> (20, -1) and run the code, you should expect there to not be any intersections. Yet, the results show an intersection at (20,0), which is totally wrong.

Potential problems:

-If two lines are the same, you get infinity results. If you're only expecting one X and Y value, this could be problematic.

-If two lines are parallel, you get infinity and NaN results (you're dividing by zero). This could also be problematic if you're not testing for them.

...

Voted up, thank you on helpful tips.

I did not point some things out so this may not be obvious at first:
The first problem:

I need integer positions so eventually i would need to cast them to int and i never use it as float, so rounding down or up doesn't really matter to me.

The second problem:
I was not aware of that, thank you for pointing that out!

The first problem:

I need integer positions so eventually i would need to cast them to int and i never use it as float, so rounding down or up doesn't really matter to me.

That's a valid need, but you still want to do all your math using floating point numbers since your inputs are floats. When all of your math has been completed, then cast the result into an int (or even better, use a rounding function! casting 1.9f into an int will result in 1, not 2.).

Consider this example:
float 1/3 = 0.3333333333
1/3 + 1/3 + 1/3 = 1.0

If you cast 1/3 as a float, then do the calculations, you get 1.0, a correct answer.

(int)1/3 = 0.0
1/3 + 1/3 + 1/3 = 0.0 (wrong!)

This is a simple example, but the point is that the fractional numbers matter and add up. The same math equations can yield different results. The more fractions you write off, the more off your calculations will be. This can lead to some weird, unexpected bugs later on and you'll be squinting at your code for hours, saying "There is no error here, the math equations are perfect! The logic checks out!"