In my navigation mesh system (made of convex polygons) I want to get out a list of instructions for my AI to follow when finding a path from A to B.
From my A* implementation I get a list of edges in the mesh that the unit has to cross to get to it's goal.
The problem is now *where* on the edges it needs to cross to move the shortest distance.
Ideally it would end up looking like this:
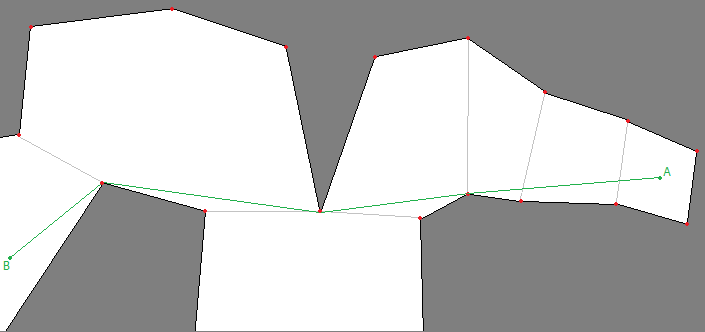
My first thought was to simply make lines to the center-points on each edge it crosses and then do an algorithm that 'relaxes' the lines and merging them if possible.
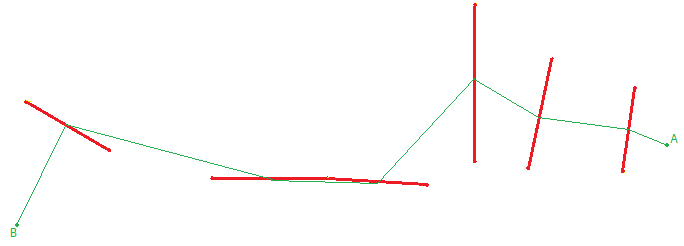
This however smells far away of a worst case O(N^2) algorithm to me (each time I merge two line segments I have to test that the new edge crosses all the edges before. N line segments that needs to have N edges validated = N^2)
Is there a better way to do this?
In the end I want to give the algorithm a radius too to avoid corners and circulate around it:
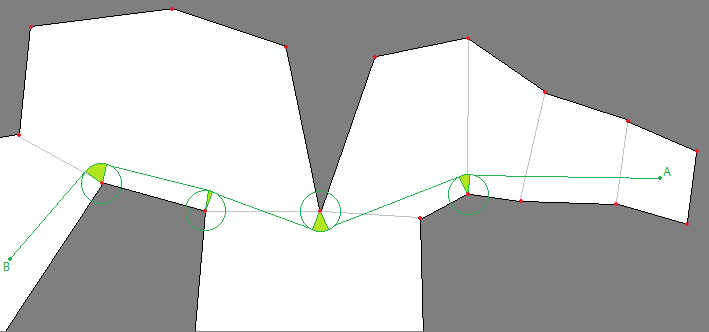
The navigation mesh needs to support any object size/radius so I cannot preprocess my mesh to be that amount smaller as for example the recast algorithm does when it generates the mesh.
My first thought is that I can simply test the point/line distance to each line-segment from the edge-endpoints and test if I need to insert an 'arc' there the object has to follow. I can figure out the points where it will enter and exit the arc using the solution to the Belt and Pulley problem.
What I am worried about is that the inclusion of a radius will alter the line segments too much that it would need to split up some lines that I already merged.
I could get around that in my initial algorithm by shortening my line segments by the radius:
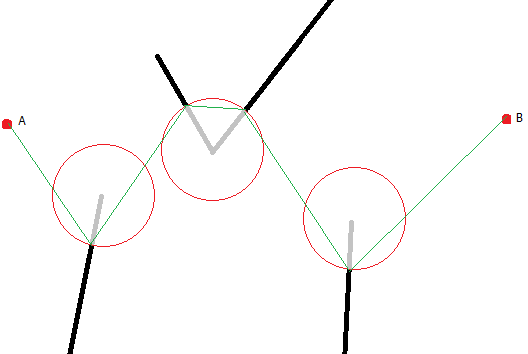
Would this work in all cases? (from there on I could collapse points on the edge of the circle into the 'arc'.
Am I overthinking this? Are there easier ways to do a smooth path though those edges?







