Abstract

In this paper I present a method for creating realistic shadows using a ray tracing technique. The technique calculates the shadows in advance and then adds them to the scene at runtime. Therefore it is not suited for real-time calculations. By using angle based theoretical sun rays the method is able to calculate the shadows shape and brightness in a realistic way. The brightness of the points in the shadows is calculated using a greyscale that simulates the amount of light reaching the different points. To simulate the influence the points have on each other the shadows are blurred. The technique is mainly focused on creating realistic shadows but simplicity is also an important factor.

1. Background

1.1 Introduction

Shadows are a common part of the world. Adding them to your 3D graphics will add a whole new degree of realism. Without shadows scenes often feel unnatural and flat which confuses the viewer. Over the year several techniques have been developed to create these important shadows.

There are two main approaches for shadow calculations: real-time shadow calculations and static shadow calculations. Using a real-time technique shadows are recalculated every frame whether or not the scene has changed. This way the shadows are always accurate when objects or the light sources move. However one mayor drawback to recalculating the shadows every frame is the large amount of processing power it requires, thus slowing down the rendering of the scene. To counter this calculations have to be fast, which decreases the shadows' realism. Static shadows avoid the issue of having to calculate the shadows in real-time. Instead, the shadows are calculated in advance and then added to the scene at runtime. This allows slower and more complicated calculations since the shadows only have to be calculated once during initialization.

Because terrain is static and doesn't change in shape or position there is no need to recalculate the shadows each frame. Therefore the best choice for terrain rendering is static shadows. In this paper I am going to present a way I have developed to calculate the shadows of a terrain using static shadows calculations. By calculating the shadow based theoretical sun rays the method will be able to create smooth and realistic shadows. The method is characterized with the following features:

• Vertical angle based calculations. Giving great flexibility in the positioning of the light source. Offering the ability to simulate different times of a day.
• Soft shadows. The shadows brightness is based on a greyscale. Simulating the amount of light reaching the different points. Giving the shadows more depth and greatly increasing the amount of realism.
• Static shadows. Shadows only have to be calculated once which increases the performance of your engine.
• Not bound to any specific API. The method may be implemented in almost any terrain engine.
• Basic calculations. Making this method a good alternative for both beginners and more advanced programmers.

2. The Algorithm

2.1. Basic Shadows

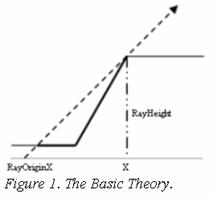
The ray lighting method draws a theoretical ray with an specific angle from each point on the x-axis. It then checks each point on that ray starting from the shadow's maximum width (based on the heightmap's highest point) against the heightmap to see if the terrain intersects the ray. If it does this point will cast a shadow on each point that precedes it that is below the ray. Figure 1 should give you a better understanding.

The method needs a way to calculate the rays' height at different points. For this it uses some trigonometry.

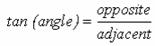
This leads to the following equation:

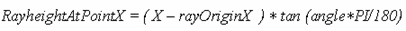
The tan function uses radians for calculation and there has to be made some changes for use of degrees. A full revolution, 360 degrees is the same as 2?. To convert from degrees to radians it has to multiply the angle by the fraction (360/2?) or (180/?).

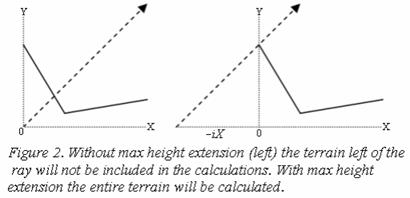
Since the ray is not a vertical line the method can't stop calculating the RayOriginX when it reaches 0. Terrain won't be included if the terrain is higher than the ray at 0. Since the ray never is vertical there will most certainly be terrain that is not included. To prevent this the calculation needs to continue in the -X direction. The distance it has to go is calculated with the following equation:

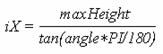
Figure 2 illustrates the problem and its solution.

2.2. Soft Shadows

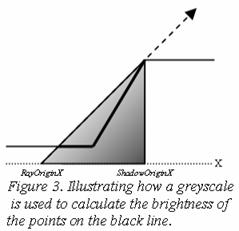
Since different amounts of light reache the ground at different points the different points will have a different amount of brightness. If this is not included in the calculations the shadows will look flat and non-realistic. To simulate the amount of light intersecting the different points a greyscale is used from which the brightness is calculated. This will make points closer to the shadow's origin darker than the ones further away, giving the shadows more depth and making the terrain's outline more visible. Figure 3 illustrates this.

The shadow starts from ShadowOriginX which is the x-coordinate of the highest point that intersects the ray. To keep all the shadows' brightness the same regarding their height, position, etc., a constant greyscale using the coordinates within the current greyscale is used to calculate the different points' brightness. This is shown in Figure 4.

Two variables are needed to hold the x-coordinate of the shadow's origin (ShadowOriginX) and the shadow greyscale's height (ShadowY). Then a variable is used for the greyscale's maximum brightness (because it should be able to modify the shadow's brightness). Then there is an equation to calculate the brightness of the different points.

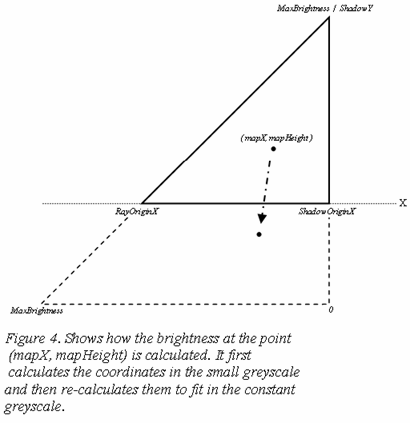
The equation calculates the x and y-coordinates for the point in the small greyscale. It then divides them with the greyscale's x and y-sizes to get a percentage of the entire greyscale, then multiplies that percentage with the maxBrightness value which is the constant greyscale's size.

These are not physically correct calculations but they give very realistic results. They give the shadows more depth and blends the shadows into brighter areas.

2.3. Shadow Blurring

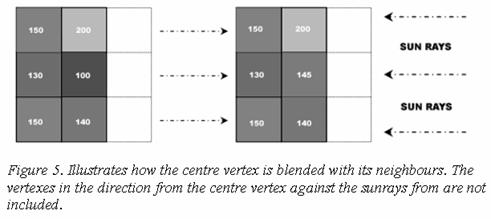
The sun is a large light source causing the shadows to be blurred. The shadows will be blurred by getting the mean value of all the points in the shadow and its neighbours. This way the points get a bit brighter or darker depending on the brightness of surrounding points. The points in the direction of the sun won't be a part of the calculations since they don't reach the shadow.

3. Implementation

3.1. Variables

/////////////// /* Variables */ /////////////// 
// Tells if there is a shadow. 
bool Shadow; 

// Holds the coordinates for the shadow greyscale. 
int ShadowOriginX; int ShadowY; 

// Hold the values for the rays' height and the terrain-maps' height. 
float RayY; 

// Coordinate positions variables. 
int RayOriginX, MapX, z, MapY; 

// The angle in which the rays intersect the x-axis. 
int Angle = 45; 

// The max height on the terrain-map. 
int MaxMapHeight = 255; 

// The max shadow brightness and. 
int MaxShadowBrightness = 255; 

// The size of the terrain 
int MapSize = 128; 

/* Pre-calculations */ 

// Get the tan value for the angle that is used. 
float TanAngle = float( tan(Angle*3.14159/180) ); 

// Calculate the maxHeightExtension 
int MaxHeightExtension = int(MaxMapHeight/TanAngle); 

// Set all points on the lightmap MaxShadowBrightness 
for (z = 0; z < MapSize; z++){
    for ( MapX = 0; MapX < MapSize; MapX ++){ 
        LightMap[MapX][z] = MaxShadowBrightness; 
    } 
} 

3.2. Shadow Calculations

///////////////////////// /* Shadow Calculations */ ///////////////////////// 
/* Ray Lighting */ 

// Loop through the z-axis. 
for ( z = 0; z < MapSize-1; z++ ){ 
    // Loop through the x-axis. 
    for ( RayOriginX = MapSize-1; RayOriginX > -(MaxHeightExtension); RayOriginX-- ){ 
        
        // Reset the shadow values. 
        ShadowOriginX = 0; 
        Shadow = false; 
        
        // If the shadow's maximum width exceeds the mapsize set MapX to mapsize. 
        if (RayOriginX + MaxHeightExtension +1 > MapSize){ 
            MapX = MapSize; 
        }
        // Else set MapX the shadow's maximum width. 
        else{ 
            MapX = RayOriginX + MaxHeightExtension +1; 
        } 
        
        // Loop through the ray from the shadows maximum width until it 
        // reaches the rays' origin. 
        while( MapX > RayOriginX && MapX > 0){ 
            // Get the height values. 
            RayY = float( MapX-RayOriginX * TanAngle ); 
            MapY = HeightMap[MapX][z]; 
            
            // If the MapY intersect the Ray there will be a shadow. 
            if ( RayY <= MapY){ 
                // Set the shadows' origin X coordinate. 
                ShadowOriginX = MapX;
                
                // There will be a shadow. 
                Shadow = true; 
            } 
            // Else if MapY is lower than RayY and there is a shadow. 
            else if ( Shadow ){ 
                // Get the shadow greyscales height. 
                ShadowY = HeightMap[ShadowOriginX][z]; 
                
                // Calculate and set the brightness. 
                LightMap[MapX][z] = unsigned char( 255 * (float(ShadowOriginX-MapX)/ (ShadowOriginX-RayOriginX) + MapY/(float)ShadowY) ); 
            } 
            
            MapX--; 
        } 
    } 
} 

/* Blurring */ 
// Loop through the z-axis. 
for ( z = 0; z < MapSize-1; z++){ 
    // Loop through the x-axis. 
    for ( RayOriginX = 0; RayOriginX < MapSize-1; RayOriginX++){ 
        // If the point isn't already lighted. 
        if (LightMap[RayOriginX][z] != MaxShadowBrightness){ 
            // Get the mean value of vertex and set the brightness. 
            LightMap[RayOriginX][z] = ( LightMap[RayOriginX-1][z+1] + 
                                        LightMap[RayOriginX][z+1] + 
                                        LightMap[RayOriginX-1][z] + 
                                        LightMap[RayOriginX][z] + 
                                        LightMap[RayOriginX-1][z-1] + 
                                        LightMap[RayOriginX][z-1] ) /6; 
        } 
    } 
} 

3.3. Colouring the Light Source

To simulate a warm red sunset or add a bit of a mystic blue light to a scene the brightness values have to be modified. The shadows becomes coloured by multiplying the brightness value for red, green and blue with the specified amount of colour. Using the equation Intensity = brightness * colour, the colour values are sent to the API:

ColorToAPI ( (GetBrightnessAtPoint( x, z ) * Red ), (GetBrightnessAtPoint( x, z ) * Green), (GetBrightnessAtPoint( x, z ) * Blue ) ); 

3.4. Horizontal Rotation

By inverting the coordinates the light source will be rotated. To rotate the light source 180 degrees and set the light direction X+, calculations of RayOriginX start from MapSize towards 0 and MapX from 0 towards RayOriginX.

for ( RayOriginX = -(maxHeightExtension); RayOriginX < MapSize-1; RayOriginX ++ ){ 
    for ( MapX = RayOriginX; MapX < RayOriginX + maxHeightExtension+1 && MapX > 0; MapX++ ){ 

To calculate in the direction of Z+ or -Z the x and z variables have to be exchanged.

        MapY = HeightMap[z][MapX]; 
        ShadowY = HeightMap[z][ShadowOriginX]; 
        LightMap[z][MapX] = 200 * ( float(shadowX-x2)/float(shadowX-x1)+ MapY/ShadowY ); 

This will allow the light source to rotate 90 degrees horizontally. However this is not the best way to do it. The heightmap and textures may be rotated and the shadows then calculated which would give the same results as rotating the light source.

3.5. Optimizations

Without soft-shading some optimizations are possible that will sacrifice quality for performance. Faster calculations may decrease the initialization time of the application.

/* Optimized Ray Lighting */ 
// Pre set the brightness. 
Brightness = 200; 

// Loop through the z-axis. 
for ( z = 0; z < MapSize-1; z++){ 
    // Loop through the x-axis. 
    for (RayOriginX = MapSize-1; RayOriginX > -(MaxHeightExtension); RayOriginX --){ 
        // Reset the shadow value. 
        Shadow = false; 
        
        // If the shadows maximum width exceeds the mapsize set MapX to mapsize. 
        if (x1+ MaxHeightExtension +1 > MapSize){ 
            MapX = MapSize; 
        } 
        // Else set MapX the shadow's maximum width. 
        else{ 
            MapX = x1 + MaxHeightExtension +1; 
        } 
        
        // Loop through the ray from the shadows maximum width until it 
        // reaches the rays' origin. 
        while(MapX > RayOriginX && MapX > 0){ 
            // Get the height value. 
            RayY = float((MapX-RayOriginX) * TanAngle); 
            
            // If the MapY intersect the Ray there will be a shadow. 
            if ( RayY <= heightmap[MapX][z]){ 
                // There will be a shadow. 
                Shadow = true; 
                
                // If all the previous points are already shaded and there will be a 
                // shadow then set MapX the previous point. 
                if (lightmap[RayOriginX+1][z] == 150){ 
                    MapX = RayOriginX +2; 
                } 
            } // Else if MapY is lower than RayY and there is a shadow. 
            else if (Shadow){ 
                lightmap[MapX][z] = Brightness; 
            } 
        
            MapX--; 
        } 
    } 
} 

4. Results

The algorithm has been added to a demo from the book "3D Terrain Programming" by Trent Polack. The shadows shapes become similar to the objects casting them. Using soft-shading and blurring they blend out into the surroundings and become a natural part of the scene. The light source has great flexibility in vertical rotation but not as much in horizontal rotation. Using the optimized implementation the performance was increased by 21% at the sacrifice of soft shading.

4.1 Images

The following screenshots are taken using the demo and demonstrate the appearance of the shadows. The shadows are calculated using a ray intersecting the x-axis at 70 degrees and a maximum brightness of 200.

5. Acknowledgements

A special thank goes to my family and all my friends who have supported me with many comments and ideas.

6. References

[1] Trent Polack, Focus on 3D Terrain Programming.

[2] Matthew Strathan, Real-Time Heightmap Self-Shadowing Using the Strider Technique.

[3] Mircea Marghidanu, Fast Computation of Terrain Shadow Maps.

[4] Charlie 'Chazz' Van Noland, Slope Lighting Terrain.

[5] Kevin Hawkins, Dave Astle, OpenGL Game Programming.

[6] Wendy Stahler, Beginning Math and Physics for Game Programmers.