Introduction
In open landscape games, rivers can add a realistic touch to the look of the terrain. I am going to discuss a method for adding rivers to randomly generated terrain that adds this realistic touch we are looking for. Unfortunately, when we are dealing with random terrain this is not always a menial task. In real life the terrain is usually formed by water carving away at the land and forming valleys and other such terrain features. When generating terrains in a decent load time, however, we don't have this luxury. My final project at Full Sail was a real time tactical game called Liege on random generated terrain with rivers. Throughout this article I am going to discuss the methods I took to create rivers for Liege.


The plan of attack
First we need to formulate a plan of attack. The method that I discuss here is the one that I decided to implement as it best suited my targeted river idea. The goal of my river implementation was to create a single non branching river that passes through a territory in a realistic looking fashion. Using this goal we know that the river will begin and end on an edge of the map as it is only passing through the territory not beginning in it. Another thing we know is that water likes to flow downwards as it would be defying gravity to flow upwards. This implementation brings simplicity to the process while still adding key detail to the map.


What do we need?
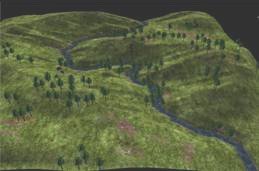To pull this off we are going to need a couple key algorithms:

• A path finding algorithm to determine the path of the river.
• An algorithm to cleanup the terrain around the river.
• A riverbed carving algorithm. Many of these may vary depending on the overall look you are trying to achieve with your river but I will step through the basics and what I have done to accomplish the look I have been going for.
  
  
  The Path
  The path is a key part of the entire process, as a river that doesn't follow a realistic path doesn't appear very river like at all (unless you are going for a non traditional world's river). In order to achieve our goal with the above mentioned restrictions the first thing we do is create a height sorted array of all the edge vertices on the map. In order to assure that we will pick a path that goes downhill whenever possible we will randomly pick our starting point from the higher 3/5[sup]th[/sup] of the edge vertices and a goal point from the lower 1/5[sup]th[/sup] of the edge vertices. The only other restriction we are going to place on the starting and ending points is that they must be on different edges of the map, using two points on the same edge will often result in a very small river that wont look right on the edge of the map. If you are using a smaller size map say for instance 257*257 vertices and you would like to increase your chances of a decent river it is suggested you further restrict the starting and ending points to be on opposite edges.
  
  Now that we have our starting and ending points of our river we need a way to calculate the path. To do this we are going to use to our advantage the fact that water is subject to gravity. Altering a simple 'best first' path finding algorithm to use a heuristic that weighs neighboring nodes by their height as apposed to distance to the goal we can get a fairly realistic path. In efforts to more heavily penalize water from going uphill it is also suggested you add an additional penalty to the heuristic anytime the new node has a higher height than the current node.
  
  Several problems will arise with the path that has been formed. The first problem with the path is that the terrain was not formed with a river in mind and so it is not always possible for the river to make it from start to end without going at least slightly uphill. We will need to alter the terrain to allow the river to always realistically flow downwards but more on this in a bit. Another problem with the path is that when the path intersects and edge of the map before reaching its end point it has a tendency to stick to the edge as it has no terrain to travel to outside the edge of the terrain and chances are if it was driven to the edge of the map then it is lower then the inside of the map. This leads to sections of river "sticking" to the edge of the map.
  
  
  Cleaning up the path
  One of the uglier side effects of the "sticking" to the edge of the map is that the river tends to do "hops" where it hits the edge, then breaks off, then hits the edge then breaks off again. Sometimes it may look like a hop is merely the river coming back from somewhere off terrain but at other times it just looks horrible. In addition to this at the mention of hops the A.I. programmer cringed, so as a solution I suggest you loop through the river nodes looking for the longest hop in the river. In the case where you don't ever hit the edge between the start and goal nodes there will only be one hop which is of course the longest. Once you have located the longest hop, merely eliminate the nodes from all the other hops.
  
  Another ugly artifact is the hop's cousin. This is where the river gets within the rivers width of the edge of the terrain and also results in visible hops although not physical ones path wise. This, however, is rather easy to fix. I merely looped through the river and tested each node's relative closeness of the edge of the map, if it was too close I merely moved it inwards. The rivers path should look realistic enough that pushing in these few nodes will not look bad.
  
  Now that we have the actual path refined we will need to adjust the height of the path, currently it is laying on the surface of the terrain. What we want to do is move each vertex down along the y axis to either its current position minus half the river depth or a hair lower than the previous vertex, whichever is lower. In doing this we assure that the rivers path is always flowing downwards. As we have each of these new heights we will also want to adjust the stored height in the height map for each corresponding river vertex, doing so will scrape the path into the terrain if you will.
  
  for ( i = m_vp3River.size()-1; i >= 0 ; --i ) { // Convert the vertices coordinates to heightmap coordinates int iRX = int(m_vp3River.x/m_MapInfo.fScale), iRZ = int(m_vp3River.z/m_MapInfo.fScale); // Lower the vertices half way down m_vp3River.y -= HALFDEPTH*m_MapInfo.fScale; // If we actually went up (water doesn't go up) // then move us slightly lower than the previous vertex if (i < (m_vp3River.size()-1) && m_vp3River.y >= m_vp3River[i+1].y) m_vp3River.y = m_vp3River[i+1].y-(0.01f*m_MapInfo.fScale); // store the new height in the heightmap m_fHeightMap[iRX][iRZ] = m_vp3River.y; }
  Carving the path
  Now that we have our refined river path, and even scraped the basis of the path into the terrain we need to carve the path. In order to combat any sudden drops we are going to carve a river bank into the terrain around the river, before we actually carve the river bed into the terrain. To achieve this riverbed I traversed through the list of river nodes and for each one I cycled through all terrain vertices within a square distance and found the slope of the line from the current river vertex to the current height map vertex being evaluated. If the slope was too high I merely reduce the height of the terrain. We repeat this cycle until all of the terrain surrounding the river is at a height we find adequate. An alternative to repeating the cycle could be to merely set the height the first time, but this tends to look more artificial and too uniform.
  
  for ( i = m_vp3River.size()-1; i >= 0 ; --i ) { // Convert the vertices coordinates to heightmap coordinates int iRX = int(m_vp3River.x/m_MapInfo.fScale), iRZ = int(m_vp3River.z/m_MapInfo.fScale); // repeat variable bool bAltered = true; while ( bAltered ) { // Our default assumption is that we don't change anything // so we don't need to repeat the process bAltered = false; // Cycle through all valid terrain within the slope width // of the current position for ( int iX = max(0,iRX-SLOPE_WIDTH); iX < min(m_MapInfo.iSize,iRX+SLOPE_WIDTH); ++iX ) { for ( int iZ = max(0,iRZ-SLOPE_WIDTH); iZ < min(m_MapInfo.iSize,iRZ+SLOPE_WIDTH); ++iZ ) { float fSlope; // find the slope from where we are to where we are checking fSlope = (m_fHeightMap[iX][iZ] - m_fHeightMap[iRX][iRZ]) /(sqrt((iRX-iX)*(iRX-iX)+(iRZ-iZ)*(iRZ-iZ))*m_MapInfo.fScale); if ( fSlope > SLOPE_VAL ) { // the slope is too big so adjust the height and keep in mind // that the terrain was altered and we should make another pass m_fHeightMap[iX][iZ] -= HEIGHT_ADJ*m_MapInfo.fScale; bAltered = true; } } } } } This will give us a nice V shaped depression along the path of our terrain. This depression will be based on the half river depth height which we lowered all the river vertices too, not the bottom of the river bed. This is why we didn't lower all the river vertices to the bottom of the riverbed just yet. As some of you may guess this filter we just ran along the path of the river has its side effects and not good ones to say the least. At the edge of the riverbank depending on how far down we are carving into the terrain there may be some quite severe dips in the terrain. This shows mostly in longer rivers where the height was slowly decreased as it went to keep it flowing down, eventually this adds up and some terrain carving can be quite severe. Now one could possible use this to their advantage depending on the effect they are going for along the river, say for instance trying to carve the Grand Canyon, but it didn't really go for the rolling hills theme of my terrain so I will discuss a way to get rid of this nasty artifact. It is actually quite simple. To fix this we will merely cycle through every vertex on the terrain and compare it to each of its four neighbors. If there is too drastic a change in height, then the current vertex is lowered to some amount less than the max difference allowed. We will have to repeat this filter over and over until the desired effect is reached. In my case I wanted all sudden drops eliminated not just worn down so I had to loop through it until no more changes were made. This method is actually quite inefficient but it was not the bottle neck of my load time, however on larger terrains with longer rivers it certainly would be. I am quite confident, however, that an algorithm could easily be formed that smartly expanded from the river over and over until everything was satisfactory as apposed to covering the entire terrain.
  
  Some example code follows:
  
  // Initialize the acceptable height changes in the terrain // this will affect the smoothness float fDeltaY = 0.5f*m_MapInfo.fScale; float fAdjY = 0.3f*m_MapInfo.fScale; // Initialize the repeat bool to run once bAltered = true; // loop while we are making changes while ( bAltered ) { // assume we aren't going to make changes bAltered = false; // for the entire terrain minus the last row and column for ( int x = 0; x < m_MapInfo.iSize-1; ++x ) { for ( int z = 0; z < m_MapInfo.iSize-1; ++z ) { // Check our right and our north neighbors if ( m_fHeightMap[x][z]-m_fHeightMap[x][z+1] > fDeltaY ) { m_fHeightMap[x][z] -= fAdjY; bAltered = true; } if ( m_fHeightMap[x][z]-m_fHeightMap[x+1][z] > fDeltaY ) { m_fHeightMap[x][z] -= fAdjY; bAltered = true; } } } // for the entire terrain minus the first row and column for ( x = m_MapInfo.iSize-1; x > 0 ; --x ) { for ( int z = m_MapInfo.iSize-1; z > 0; --z ) { // check out our south and left neighbors if ( m_fHeightMap[x][z]-m_fHeightMap[x][z-1] > fDeltaY ) { m_fHeightMap[x][z] -= fAdjY; bAltered = true; } if ( m_fHeightMap[x][z]-m_fHeightMap[x-1][z] > fDeltaY ) { m_fHeightMap[x][z] -= fAdjY; bAltered = true; } } } } Now the terrain is ready for our riverbed. This is actually the simplest part; all we simply do is cycle through each vertex of the river and lower all height map vertices within a certain radius to a height less than that of the current river vertex. How much you lower it depends on the depth of the riverbed you are going for. This particular carve can leave some sharp edges but because of the riverbed the sharpness of the edges is already fairly small and can easily be smoothed out with a bilinear filter across the terrains heights. That is pretty much it as far as our actual river carving is concerned. There are so many spins one could apply to these algorithms to create different effects. I have found that in my implementation, it actually carves quite a bit of detail into an otherwise fairly plain terrain.
  
  A note about the riverbed carving, because I carve a square pattern at each river node into the height map not only can it be wasteful time wise but it also causes some step like diagonals in the riverbed. One thing I did to fix this blemish is I go through the river nodes on last time and I average out the heights along the edge of the bed whenever moving diagonally across the map. I found this to be faster than handling it when carving the riverbed as it allowed me to make more assumptions in both cases but results may vary with longer rivers.
  
  
  Level of detail and other considerations
  It isn't too uncommon now a day if not downright required for terrains to be rendered using levels of detail. If using a level of detail algorithm that takes the ruggedness of the terrain into consideration giving more detail where needed, such as the ROAM algorithm, it shouldn't have as much of an impact on the river. If however you are using a simpler method such as geomipmapping, I have found you need to restrict the detail levels of the patches containing portions of the river. Often enough if you don't the terrain will be over simplified in a current patch completely eliminating any obvious sign of the river. This may or may not be a problem depending on your camera angle and how fast you move throughout the world.
  
  
  
  Creating the water
  Creating the water can be quite a tricky task, depending on whether you want it to flow or move up and down, adapt to the LOD or merely remain static. The actual simulation of flowing water is beyond the scope of this article, however, I will cover a very simple way to simulate a static triangle strip of water for this newly formed river. In actual implementations you might want to break it into different triangle strips per terrain patch and adapt it with the current LOD. The first thing we must do is recognize that although it is a seemingly random river there is still a systematic method to its madness. If we always start at one end of the river and traverse through the list of nodes we can visualize each needed vertex in a triangle strip alternating from our right and our left as we traverse the nodes, the real question here is how we figure out their positions.
  
  Let's first lay out some assumptions, we will be traveling from the high end of the river to the low end and we will be creating our triangle strip in a right, left, right, left, ... clockwise fashion. In order to calculate the orientation of the particular vertices we are going to use a little bit of linear algebra, however we will be able to keep it all in 2D space making it much easier. If we imagine a line passing through our current position from where we were to where we are going we will have an approximation of our current orientation (which way the water is flowing). While standing in the middle of the river facing along the direction of orientation the width of the river will be to our left and right. In other words the width of the river will be perpendicular to our orientation. So to find the position of the vertices for our current position we will move out half the rivers width in both directions perpendicular to our orientation. Because we are simplifying the entire process to 2D we can easily represent the perpendicular line as one with the negative inverse slope of our current line. Following is some sample code to hopefully explain the process a little bit better.
  
  // Calculate the perpendicular vector v2Norm.x = -(m_vp3River[i+1].z - m_vp3River[i-1].z); v2Norm.y = (m_vp3River[i+1].x - m_vp3River[i-1].x); v2Norm *= 1.15f*0.5f; // Project our right point our along the normal v3Pos1.x = m_vp3River.x + v2Norm.x*(Width/2.0f); v3Pos1.z = m_vp3River.z + v2Norm.y*(Width/2.0f); v3Pos1.y = m_vp3River.y + Depth*0.4f; // project our left point out along the negative normal v3Pos2.x = m_vp3River.x - v2Norm.x*(Width/2.0f); v3Pos2.z = m_vp3River.z - v2Norm.y*(Width/2.0f); v3Pos2.y = m_vp3River.y + Depth*0.4f; What we see above is v2Norm is defining our perpendicular vector by using the negative/inverse slope of the orientation vector. In this case I negated the delta z of the orientation vector, which one you negate is relative to your winding and which way you are traversing through the river. You may notice that I multiply the normal by 1.15 to slightly extend the projection for the water to slightly stick into the side of the riverbed preventing gaps. I also multiply it by 0.5f which is to accommodate for the fact I am not normalizing the vector. Normalizing the vector would be a more accurate representation but I found an unnecessary slow down in most instances. You can also see that I setup two vertices with this data. This merely shows how we take into consideration our current position and the river width vector. Also I have not yet mentioned how I am initializing the height of the vertices, in this case I stuck with a very simple static height compared to the bottom of the river. Since we used a depth variable twice once to carve the river shore and again for the bed I chose to multiply the depth by 0.4 as it is slightly less than half the depth and therefore shouldn't be hovering above the riverbed. Traversing through the entire river this should form a decent static water surface following your newly carved riverbed. Obviously this method does not take into consideration of LOD nor animated water. You would also want to take special precaution of the edges of the rivers as orientation can't be calculated with both the vertices in front and behind you.
  
  
  Conclusion
  Carving random rivers into a random terrain is not an easy task, what I have presented here is only one of many ways we can accomplish this task. Rivers can add a wonderful change in scenery in an otherwise regular terrain, often adding character and depth. Through breaking down the idea into smaller parts and analyzing what our goals are we can easily move towards accomplishing what we are looking for. This article does not describe the fastest method, the best method, or even the most realistic method for creating rivers but instead presents us with a good base to establish the style we are looking for.
  
  This article was the result of a months worth of research while at Full Sail for my final project Liege and this was the resulting process I used, however there were many more looks and styles one can use by changing different parts of the process. I would encourage everyone to try different path finding algorithms like Dijkstra which can result in pooling, similar to that of small lakes. For a glimpse at how I went about creating this process you can go here, it also includes some information regarding how I later placed trees on the terrain. If anyone has any questions or suggestions about the article feel free to [email="dave@dclyde.com"]email[/email] me or post in the forums. I will be sure to take the time to read them all, hopefully I will get around to doing a couple more articles benefiting from your comments when I find another topic.