There is a C++ library called TetGen. I’m trying to obtain the Voronoi diagram of a tetrahedralization. I know how to get the face count, but how do I know how many vertices make up each face?

taby said:
I’m trying to obtain the Voronoi diagram of a tetrahedralization. I know how to get the face count, but how do I know how many vertices make up each face?

Well, if you place your points at the centers of the tetrahedrons, then the voronoi regions are equivalent to the tetrahedrons themselves, no?
Thus you get 4 vertices per region. \:D/

Sorry for the late reply. I kind of got it figured out now.

Ah, so your points ar not the tetra centers, but the vertices. I see.

But i still speculate you might not need to calculate a voronoi diagram, because the data is already there.
There is the concept of a ‘dual’ mesh:

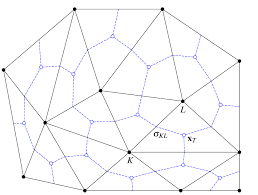
The same must exist for the volumetric version of a mesh, e.g. a tetrahedralization.

For surface meshes there are simple rules, ignoring boundary cases:
Vertices correspond to dual faces, and vice versa.
Edge count remains the same, but they rotate 90 degrees.

Yeah, I had to pull a few tricks, but the problem can be boiled down to being on the surface of a 2-sphere, like I’ve done. In the end I get triangles and their dual, the n-gons (where n is mostly 6).

I appreciate your ponderings on the matter. It makes me think in ways that I would not have otherwise done.

I’ve been messing around with TetGen’s Voronoi diagram output. The output is given sorted, instead of sequential like you’d hope for. So I had to write code to convert the sorted data back into sequential format. Also, TetGen uses random winding order, so that I have to calculate the triangle normal to make sure that it points outward from the centre of the ball.

Other than that, TetGen works like a dream!

taby said:
Other than that, TetGen works like a dream!

Try it with Sponza instead of a simple sphere… ;)

You could feasibly use a Voronoi diagram in 3-dimensions to divide the mesh into parts that act as fragments, when bombarded by rocket propelled grenades and such.

taby said:
You could feasibly use a Voronoi diagram in 3-dimensions to divide the mesh into parts that act as fragments, when bombarded by rocket propelled grenades and such.

Yeah. Such tools can be used to precalculate pieces of destruction, and game / physics engines often have them built in. Though, for that it's enough to have any convex decomposition (e.g. the V-HACD library). Does not need to be a voronoi diagram from given seed points, but if so it gives good art control. (Newton engine dev wanted to implement this many years ago - not sure if it's already in.)

Strict tetrahedralization is often used for soft body simulation.

What do you do with this?

This is my conversation with regard to:

https://gamedev.stackexchange.com/questions/164686/why-are-spherical-worlds-so-rare

Here's a screenshot of the curved hexagons, etc. So I've got the Voronoi stuff working now.

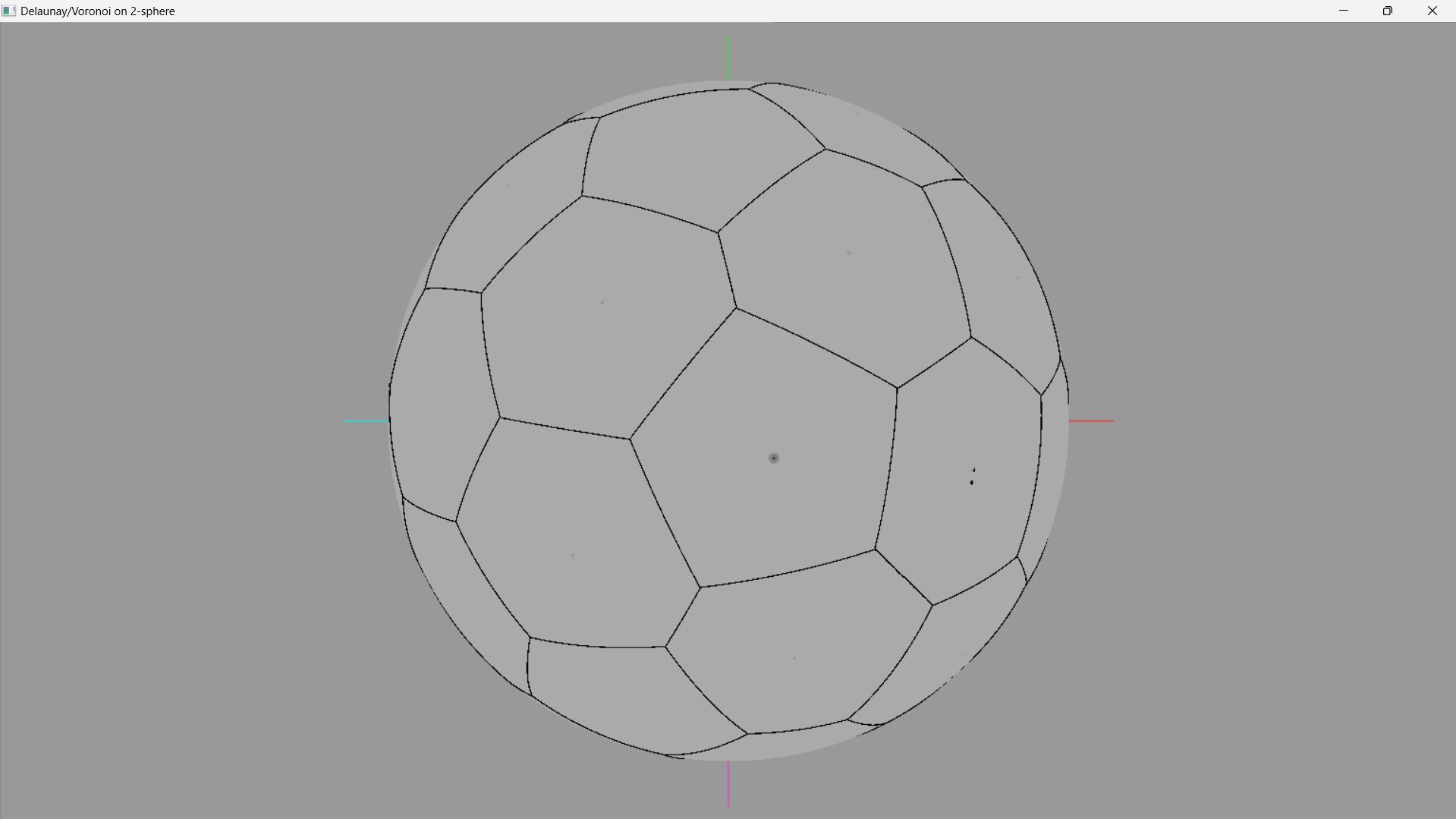
There is no use for this, perhaps maybe for a game, but this is purely an academic exercise; art for art's sake. :)