Hi, I was reviewing some of the solver theory and am a bit confused about how Sequential Impulse works with contacts. I have a working constraint solver, but still would like to understand the theory a bit better.
In the [paper](https://box2d.org/files/ErinCatto_IterativeDynamics_GDC2005.pdf), we see in the time stepping section the equation we want to solve using PGS.
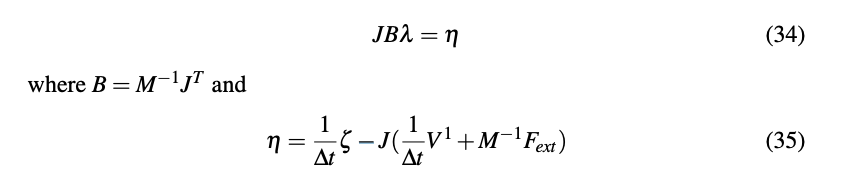
I understand this derivation. How the terms translate to the code we need slightly confuses me. I'm using the Box2D lite code as a reference: https://github.com/erincatto/box2d-lite/blob/master/src/Arbiter.cpp
My original understanding was that:
![]() : the bias. This is clearly computed on 109. and multiplied by 1/dt.
: the bias. This is clearly computed on 109. and multiplied by 1/dt.
![]()
The equation inside the brackets is the updated velocity that we compute before the solver step using the latest external forces. J computes the initial separating velocity (For contacts), which is done in every iteration of the solver, which works with Gauss seidel when solving for JB\lambda. I don't understand why the 1/dt isn't ever applied in the code to the separating velocity. It seems to be only applied to the bias term, but shouldn't it be also applied to the initial separating velocity term?
Any clarification would be really appreciated. On a side note, if anyone has some good resources for understanding the theory solvers in physics engines, that would be appreciated!







