I think I figured out a good chunk of it but I have a question. Let’s say I have a unit A at position 1,2 and two units ( B and C) placed in row at positions 2,2 and 3,2 . Unit A moves to the right and collides with unit B so unit A climbs up to position 1,1 to avoid unit B ( for simplicity let’s say the units move in right angles when avoiding other units) and then moves to the right reaching position 2,1. The goal is to get A reach the position 4,2 . The question is when unit A is in position 2,1 or 3,1 does it need to start moving towards 2,2 or 3,2 until it collides with B (or C ) or there is some automatic way to detect the presence of C at 3,2 allowing A to move directly to 4, 1 (I mean without moving every time downwards and then getting back up to continue the way towards 4,1 ). Thanks

The “automatic way” is ordinary pathfinding with B and C as obstacles, which would probably be more productive than suicide by special cases.

If obstacles are sparse, you can probably accelerate pathfinding enough to do it frequently with approximations (e.g. search to reach the original shortest path beyond an obstacle instead of the distant destination) and with appropriate data structures and algorithms: jump point search, rectangles that don't contain obstacles, cached costs, etc.

LorenzoGatti said:

The “automatic way” is ordinary pathfinding with B and C as obstacles, which would probably be more productive than suicide by special cases.

If obstacles are sparse, you can probably accelerate pathfinding enough to do it frequently with approximations (e.g. search to reach the original shortest path beyond an obstacle instead of the distant destination) and with appropriate data structures and algorithms: jump point search, rectangles that don't contain obstacles, cached costs, etc.

In a previous thread someone was saying pathfinding should not be used when the obstacle is other moving units so I was wandering what that other approach might be. Maybe I misunderstood what that person was talking about.

One problem of using pathfinding when dealing with moving obstacles is that if obstacles move you end up avoiding obstacles that are no longer there

Calin said:
In a previous thread someone was saying pathfinding should not be used when the obstacle is other moving units so I was wandering what that other approach might be.

That was me probably, proposing a simulation approach instead.
Iirc, you responded that you're not very experienced with related math, but that's not hard. In general simulation is easier than graph algorithms needed for path finding.

I can't follow your example description, you'd need to add a picture to illustrate.
But i can illustrate how a simulation approach would work. Related search terms would be ‘flock’ or 'swarm' behavior, which should give many examples.

Say we have some units, each moving at some velocity.
You would use a 2d vector to store x and y of such velocity, and you would use the same class / struct to handle points as well, e.g. the position of a unit.
Here is an example of such 2d vector class:

	struct Vec2
	{
		float x, y;

		Vec2 () {};

		Vec2 (float x, float y) : x(x), y(y) {};


		Point2D operator + (const Vec2 &p) const 
		{
			return Vec2 (x + p.x, y + p.y);
		}
		
		Point2D operator - (const Vec2 &p) const
		{
			return Vec2 (x - p.x, y - p.y);
		}
		
		Vec2 operator * (const float v) const
		{
			return Vec2 (x * v, y * v);
		}
		
		float Dot (const Vec2 &p) const
		{
			return x * p.x + y * p.y;
		}
		
		float SquaredLength (const Vec2 &p) const
		{
			return p.Dot(p);
		}
		
		float Length (const Vec2 &p) const
		{
			return sqrt(SquaredLength(p));
		}
		
		float Perp (const Vec2 &p) const // dot product with perpendicular p
		{
			return x * p.y - y * p.x;
		}
		
		Vec2 Perp () const
		{
			return Vec2 (-y, x);
		}

		float& operator [] (int i) // get x or y using given index of 0 or 1
		{
			return *(&x + i);
		}

		inline float operator [] (int i) const
		{
			return *(&x + i);
		}

	};

That's basically all you need about the math you're probably missing.

Here we have some units, moving at random velocities.
The velocity vector is illustrated with arrows.
It's just two numbers: x and y.
The longer the arrow, the faster the unit moves.
Some code to calculate the future position of a unit would be:

struct Unit
{
	Vec2 pos;
	Vec2 vel;
	
	Vec2 CalculateFuturePosition (float deltaTime)
	{
		return pos + vel * deltaTime;
	}
}

As you see, using a vec2 class we don't need to write duplicated code for the two x and y values.
So that's convenient and also easier to read.

Now, our current unit is the big dot with the green arrow.
It may collide with nearby units.
We want smarter units, tending to avoid collisions from their behavior.

To do this, we iterate all nearby units within some given radius, and accumulate their velocities to calculate an average. E.g. like this:

const float radius = 10.f;
const float mix = 0.02f;
Vec2 currPos = currentUnit.pos;
Vec2 averageVel(0,0);
float weightSum = 0.f;

for each unit
{
	Vec2 diff = unit.pos - currPos;
	float dist = diff.Length();
	if (dist >= radius) continue; // unit too far away; ignore it
	
	float weight = radius - dist; // the closer the unit, the larger the weight
	weightSum += weight;
	average += unit.vel * weight; // adding the weighted velocity to our average
}
if (weightSum > 0.00001f)
{
	averageVel /= weightSum; // divide to get the weighted average of nerby velocities
	
	currentUnit.vel = currentUnit.vel * (1.f-mix) + averageVel * mix; // change our current velocity a little bit so it converges towards the average with time
}

I have added my guess about the average velocity in blue, plus the circle from the given radius.

If we do this for all units, i expect we get something like this:

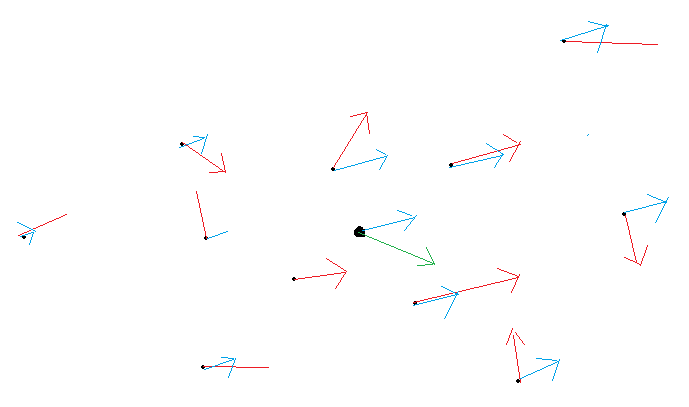
All units would move into a similar direction then their nearby units. Thus they avoid collisions by moving liek a swarm of birds.
In mathematical terms, what we do is blurring the velocity field to minimize divergence.
Which is the primary problem in fluid simulation, and so what i've just described is a very basic form of SPH particle based fluid simulation. Just fyi.

I'm pretty optimistic you can implement this with out a need to learn new math.
Combining this with a grid and path finding is possible, modeling collision response this way is possible as well, but it would take you some time and experimentation ofc. It's something new maybe, but it is not difficult in my experience. (simulating a stack of boxes under gravity would be difficult, for example)

That said, there is a problem with the simple approach i have proposed.
Consider this example:

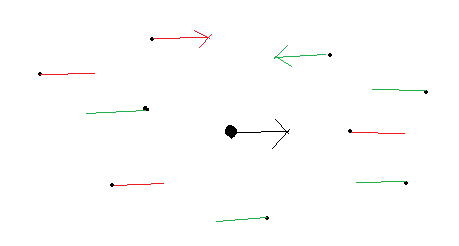
Eventually we have two factions. One moves from the left to the right, and the other moves from the right to the left.

In this case, the average of their velocity will be zero. So it will not work. They would just slow down and eventually stop.

So the simple vector field math from fluid simulations is not good enough to model this.
We would need a line field instead a vector field. Which is already a topic not commonly used in games.
For a ‘line’ it does not matter if the direction is left or right. all that matter is the angle of the line going in both directions.
The math is no longer trivial. In 3D i already need stuff like singular value decomposition of a covariance matrix made from the velocities. This works in 2D too, but is complex math.
Luckily, in 2D there is an easier way: We take the angle of each velocity and multiply it by two, so left and right gives the same angle. Then we sum those angles up, calculate the average, then divide by two to get the average direction vector, which we can nor multiply by 1 and -1 to define our line. The unit can then use the sign which is closer to its current velocity.

I can explain this in more detail when needed. For now you only need to know it can be solved. Algorithm remains the same, just some math changes.

In any case, my proposal only models a general behavior to avoid chaos.
But likely you still need some close range collision avoidance / resolution too.
But that's easy. E.g. you can model velocity so units do not come closer together than some given small radius. This could work only considering positions but ignoring velocities of other units.

Bottlenecks are an issue. Using a steering behavior to resolve almost all of it.

Pathfinding is the reasoning about how to get from point a to point b. It gives a shortest path based on whatever criteria you give it. Generally don't reason about movable objects when doing pathfinding.

Steering is about moving along that path. Steering behaviors can avoid small obstacles, maintain formations, and temporarily slow/stop to let another unit pass. Steering behaviors can also notify a stationary unit in front of them that they need to move out of the way, just like real life.

There are still some scenarios where bottlenecks cause problems to routing, especially when you need bi-directional traffic through a one-unit-wide section. One approach can be to guarantee a path is at least 2 or even 3 units wide, but even then, creative players can find ways to block up choke points. They are important for controlling movement both in real life and games.

JoeJ this is a picture for what I was trying to explain in words

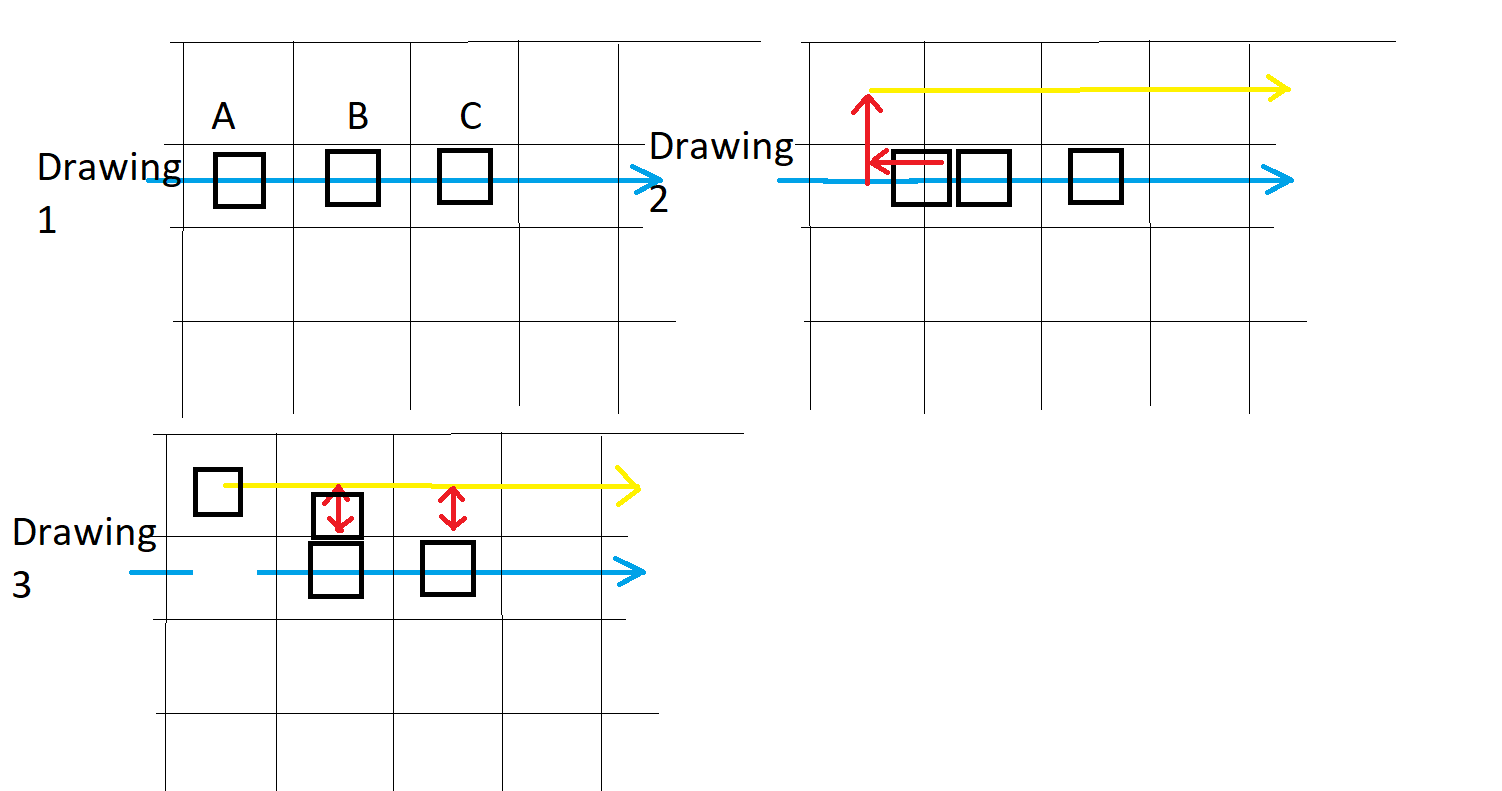
Blue line is the primary lane the path provided by pathfinder, yellow line is the secondary lane (upper lane, left lane etc.)

In Drawing 2 A collides with B goes back until it reaches the center of the tile and then moves to secondary lane and then walks on the secondary lane the length of a tile, then it tries to return to the primary lane (drawing 3 first red arrow), it collides with B and returns to the secondary lane, then it walks another length of a tile and tries to return to the primary lane again and collides again with another unit (C). My question is is there a way to avoid travelling downwards to check if there is someone there?

With regards to your post what you’re talking about is pretty much the approach to unit behavior from Total Annihilation, the units move like car simulators. In Starcraft or Age of Empires units seem confined to the grid. Under the hood it’s probably the same steering you and frob are talking about though.

frob, so steering is what I need.

Calin said:
In Drawing 2 A collides with B goes back until it reaches the center of the tile

That's bad, and you probably want to avoid the need of going back. It looks like dumb behavior to the player, and also it requires to track some complex state of ‘oops, i was running against obstacle, so i need to go back first, and after that i need to find another way around the obstacle’.

To prevent the issue, you need to check for obstacles not only the current cell, but at least the next cell as well. But ideally some amount of 3 or 4 cells, so the path to dodge the obstacle could be made smoother.

The primary limitation here is: If your units exist in only one cell at a time, and can only plan to move to an adjacent cell, smooth paths are not possible. Because they only move in angles of 90 degrees, or 45 if you allow diagonal neighbors as well. Such limitation is often desired, but more so for round based games. Realtime games usually try to avoid the quantization to the grid, or they try to hide it at least visually.

To avoid it, units can be simulated using real numbers for positions (and velocities). Simulation methods to model response to other units, collisions, etc., become possible, replacing complex logic with simple math. But each unit can be still linked to grid cells, still using path finding as usual. Behavior can also be used to smooth the paths so the 45 degree angles become less obvious. Behavior is a mix of natural physics and grid based logic, which is still predictable to the player.

To accept the grid quantization, units usually have integer numbers for position, but may have a fraction for a visual offset to generate an illusion of smooth movement. This mobile game i've made would be an example:

In this game, all enemies moved at the same speed iirc, and they could do only 90 degree turns.
Within those limitations, checking the next cell for obstacles was good enough iirc.
But if there is something in the next cell, i also needed to check its velocity. If the obstacle moves in the same direction than the unit wants to move, it's not blocking and can be ignored. That's a typical ‘devil in the detail’, but isn't hard to handle.

I think you need to decide which of those two directions you want to go. Smooth or quantized. Only then we can give specific advise, and only then you can avoid to code stuff which might be replaced later if you switch direction.

Calin said:
frob, so steering is what I need.

Probably would solve this, yes.

Often a few simple rules create emergent behaviors. For example:

1. Attempt to travel to next spot in chain.
2. If blocked: attempt to travel one square to the right of the chain and continue.
3. If still blocked and you already know it's a movable object: stop, tell the object to move and make a noise (e.g. yell, honk, beep, etc.) The “tell the object to move” makes the thing move one square in a random direction if it can.

The natural result of this if we mix of fast and slow in both directions moving right and left, the system will naturally flow into four rows: fast moving vehicles traveling left, slow moving traveling left, slow moving traveling right, fast moving traveling right. If something goes wrong you'll have a traffic jam with everything yelling and honking and the unit causing a blockage constantly scrambling out of the way, eventually the traffic jam will clear.

frob said:
Attempt to travel to next spot in chain.
If blocked: attempt to travel one square to the right of the chain and continue.

That's a good example for a typical 'quantized' grid game using logic.

For the ‘smooth’ game, the same thing would work a bit different:

The left most unit wants to move right, but is blocked by another unit standing still.

So we get a collision, and resolving it will look like:

(Colliding state in red, resolved state in green. assuming the other unit isn't affected from the collision)

So the left unit moves upwards around the obstacle, because it's initial position was slightly upwards from the blocking unit.
We do not need to decide if we dodge left or right. Because positions are real numbers, height won't be the exact same for both units, and thus it's clear where to go without any logic.
(ofc. one float can be the exact same value than the other, then we just fall back to ‘always go right’ if we use a ≥ for our comparison, or we always go left if we choose >. So we still don't need to worry or care - it does not matter in practice.)

Now i really don't say that one approach is better than the other in general. But i always think you work on the quantized approach, while what you really want is the smooth approach.
You need to clarify for yourself.