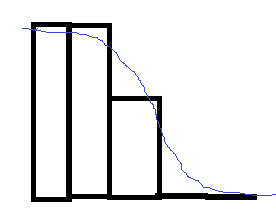
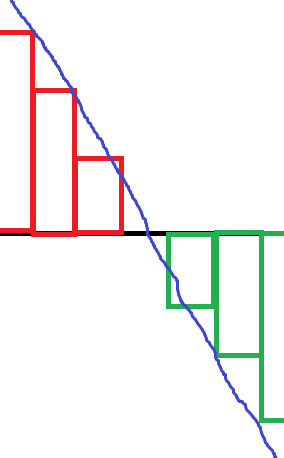
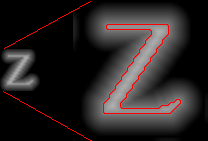
In the original Valve paper about SDF, they compare their paper to alpha-testing (as can seen in the video here or the paper here) the alpha Alpha tested version is a lot sharper than bilinear filtering, but it has a wavy like shape near edges as seen on the image to the left below:

I would appreciate if someone can point me to why it is the way it is.
On another note (which may or may not be related to the original question) why is SDF scalable, or more specifically why does interpolation works in the case of SDF but does not work in the normal case? I am mostly interested really in the math behind it, reading about it online, seems to suggest SDF is similar to Contour lines. I am not entirely sure I see the connection. Any points or links are also highly appreciated, as I feel I am lacking a lot in the basics of text-rendering.
Best,
Ali