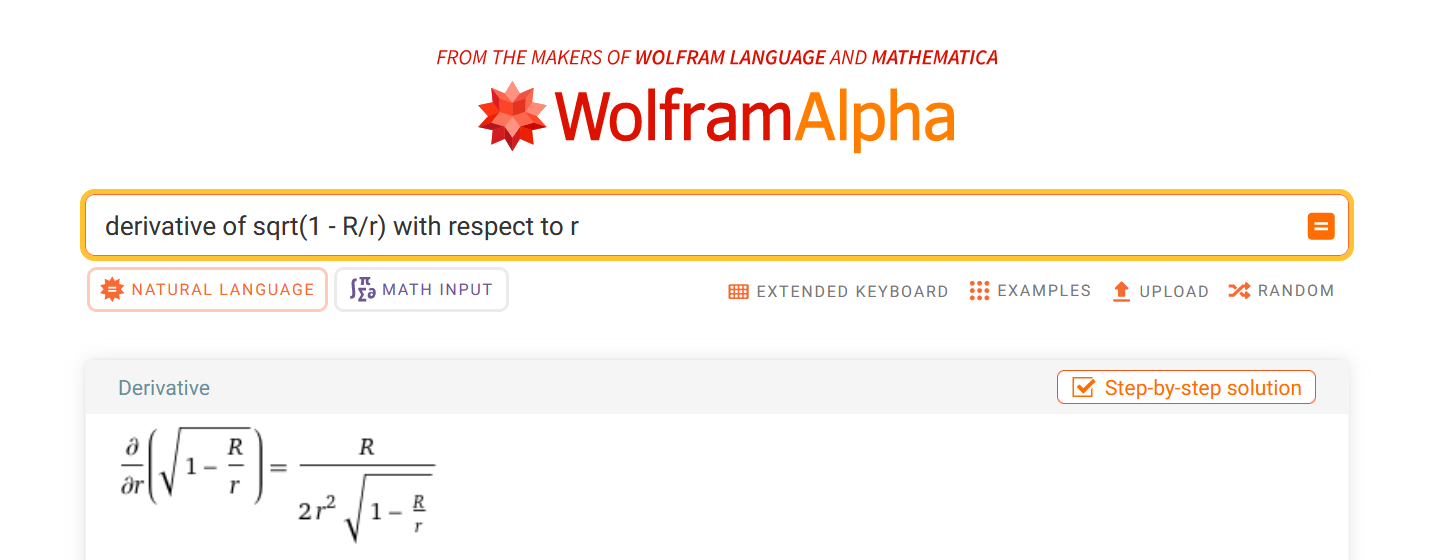
Also, instead of using Newtonian acceleration, I tried out simply using the derivative of the time dilation in the Schwarzschild solution. What I mean is that it's more natural, and it works quite fine:

void proceed_Euler(custom_math::vector_3& pos, custom_math::vector_3& vel, const long double G, const long double dt)
{
	custom_math::vector_3 grav_dir = sun_pos - pos;
	const long double distance = grav_dir.length();
	const long double Rs = 2 * grav_constant * sun_mass / (speed_of_light * speed_of_light);
	const float beta = sqrt(1.0 - Rs / distance);
	const long double gradient = (speed_of_light * speed_of_light * Rs) / (2 * distance * distance * sqrt(1 - Rs / distance));
	const float alpha = 2.0 - sqrt(1.0 - (vel.length() * vel.length()) / (speed_of_light * speed_of_light));

	grav_dir.normalize();
	custom_math::vector_3 accel = grav_dir * gradient;

	vel += accel * alpha * dt;

	if (vel.length() > speed_of_light)
	{
		vel.normalize();
		vel *= speed_of_light;
	}

	pos += vel * beta * dt;
}

Well, if the Universe is infinite in extent, then it's technically a multiverse. The reason is because there can only be a certain amount of mass crammed into a small enough space, a so-called holographic principle that limits the amount of information within a region. That means that, in infinite space, there are an infinite number of exact copies of you living your current life, and an infinite number of slightly different lives, etc, etc. So you're nothing special, just like me. )

The new paper, which uses the derivative of time dilation to calculate acceleration in the weak field, is at:

https://github.com/sjhalayka/gr_paper_2/blob/main/bezier_escape.pdf

Fascinating. I guess your integration gives realistic elliptical orbits around the sun?

But the clipping to speed of light feels fishy to me. Nature never clips. It makes me think there must be another way so the limit can never be reached.

taby said:
That means that, in infinite space, there are an infinite number of exact copies of you living your current life, and an infinite number of slightly different lives, etc, etc.

But if the universe is infinite, the amount of space is unlimited too, and so is mass and information as well?

Anyway, personally i don't have a belief regarding if the universe is infinite or finite.
But i guess if the big bang is true, it must be finite ofc.
If there is a cycle of bangs and contradictions in some form, it would be periodic, but still finite.
So, science has ruined my initial expectation about a infinite universe. But this does not mean much.
Maybe, many worlds and multiverse theories are made up from scientists who can't deal with a finite universe philosophically. No disrespect against science, but for the unknown, there seems no real difference between science, religion or philosophy. Their research might follow their beliefs, desires, convictions.

That's probably also why i say ‘we will never figure it out’, since the unknown is just another form of cozy infinity. ; )

Edit: I got your quote wrong. You mean with infinity there would be also an infinite number of exact copies, beside an even much larger infinite number of completely different things.
I know this idea, and it makes sense.
But i don't believe it.
It only works if it is at all possible to make an exact copy of anything. Which i think is not.
If Heisenbergs uncertainty is true, exact copies are impossible, no?

There is a no cloning theorem, I believe.

Anyway, yes I believe it's THE Universe, finite but super large in size.

I suspect that there's a God, and we're here for his entertainment.

Poor god. He's so lonely he attempts to entertain himself with his own creations…
I've tried that too, and it does not really work. <:/

Nasa ran a supercomputer for 5 days to make this video:

Probably i'm much more entertained from gods creations than he is from mine. : )

We should do this in a game. We're no rocket scientists, but i'm sure we could do this in realtime on a Switch, lol.

Yes, the Switch rules.

Post-Newtonian general relativity revolutionized our understanding of gravity beyond Newton's laws. It describes how massive objects warp spacetime, affecting the motion of nearby objects. This framework is crucial for precision measurements, such as gravitational waves, and for understanding phenomena like black holes, gravitational lensing, and the bending of light.

Right. Thanks for the insight.

It's not even post-Newtonian anymore. It's full-blown relativity now.

https://github.com/sjhalayka/gr_paper_2/blob/main/bezier_escape.pdf

Instead of using the Newtonian acceleration vector, we use the gradient of the gravitational time dilation. Of course, in the weak field, the two match up.