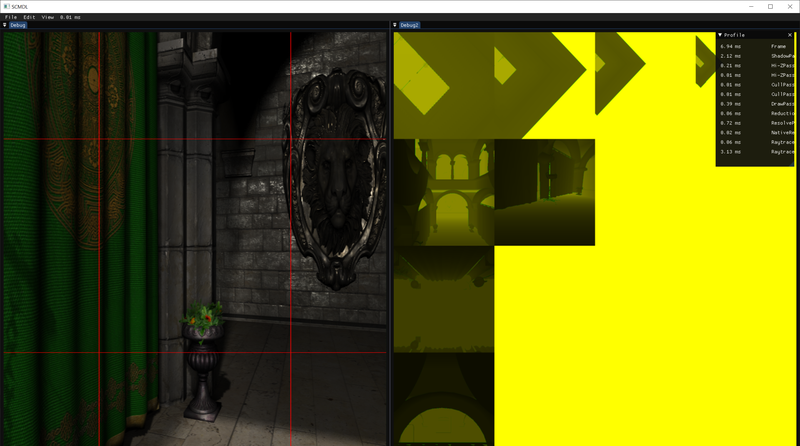
I'm trying to figure out if there exists a clever way to test if a frustum is visible in a frustum. Not even a generic way - I'm using camera frustums to be precise - each is defined by 6 planes and 8 corner points. It has to consider both cases - orthographic and perspective cases (i.e. it can't be generalized to be just OBB in either case)

My first idea was to use generic 3D SAT, which works, but that really seems like "using a nuke on an ant" ... with all of its costs. So I'm trying to figure out if there is a more clever way.

I'm considering using same approach as with AABBs - it is just going to be slightly more expensive. So the situation is like this:

To simplify the case - I sketched this in 2D (thanks Geogebra!), there are 2 frustums GHJI and OPRQ. As frustums are convex objects, the approach could be the same as is used with boxes in general (testing whether longest line along normal in the second frustum is inside the testing plane, intersects it or is outside), i.e.:

result = INSIDE

for (i = 0; i < 6; i++)
{
    if (distance(plane[i], maxPoint) < 0)
    {
    	return OUTSIDE
    }
    else if (distance(plane[i], minPoint) < 0)
    {
    	result = INTERSECT
    }
}

return result

Where minPoint and maxPoint are the points from other frustum sorted by distance to plane (negative distance meaning point being ‘behind’ the plane). When looking at in in the above scenario it yields:

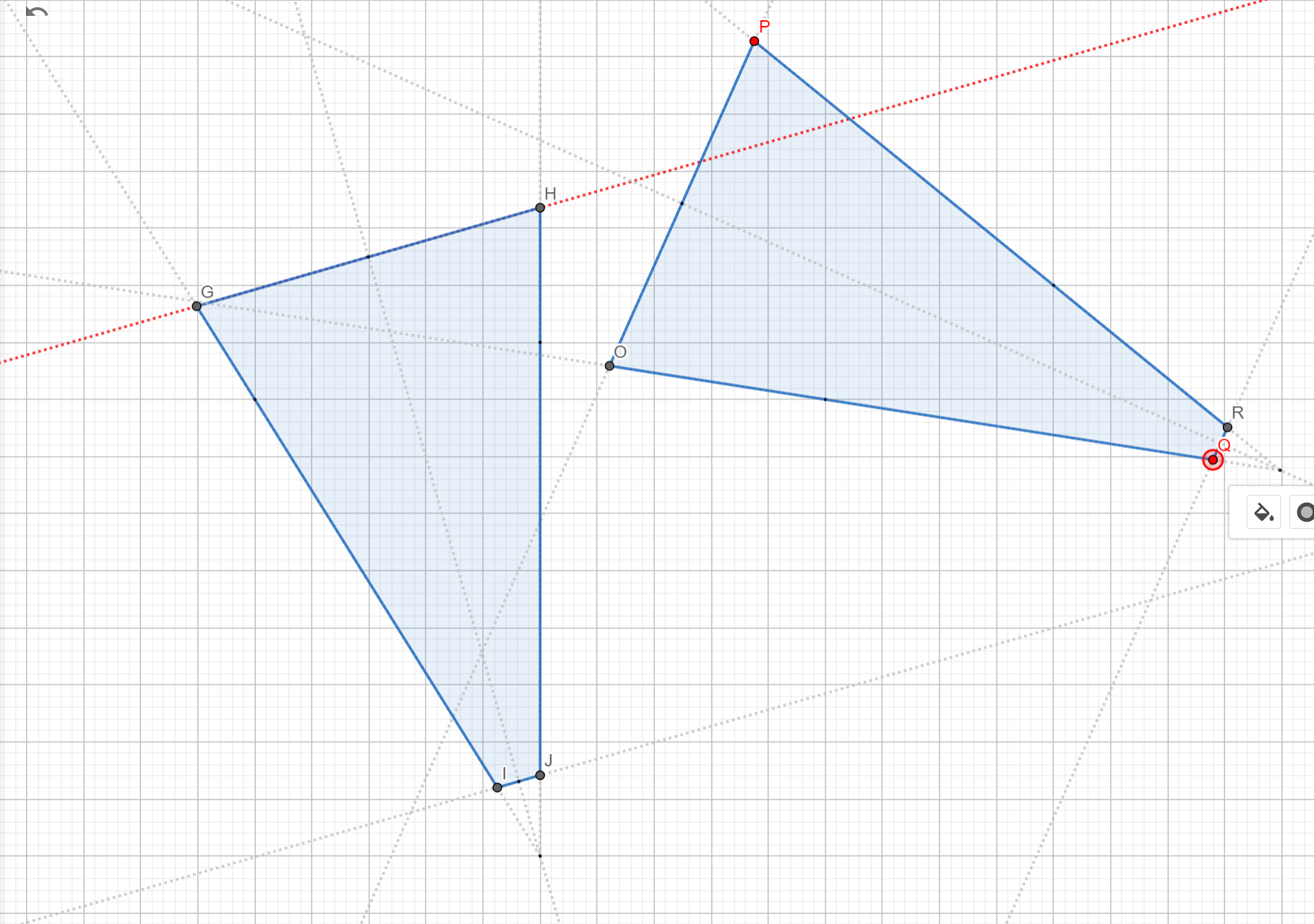
For the first plane result will hold INTERSECT.

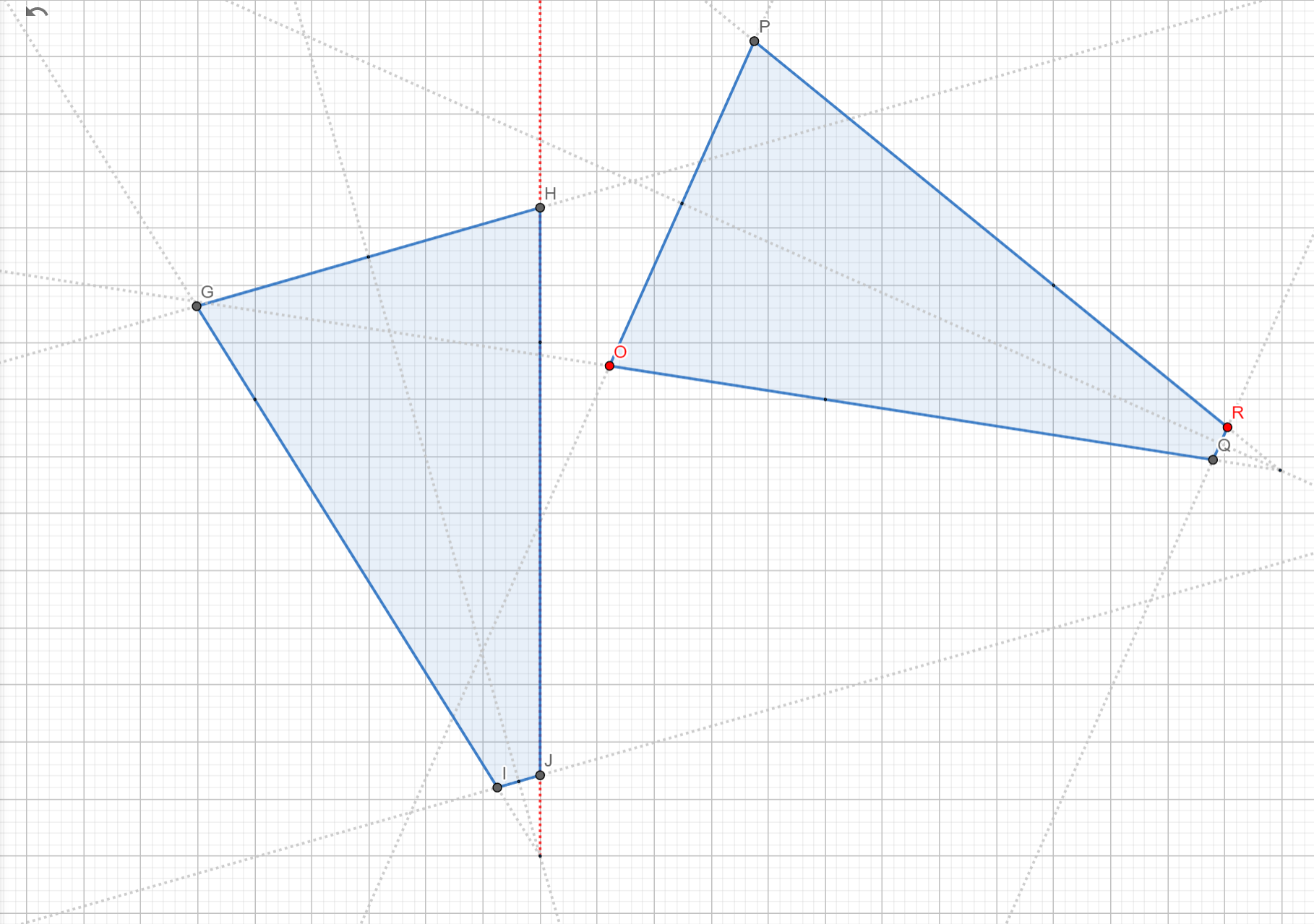
For the second plane it will straight return OUTSIDE.

I did the similar approach for the intersecting frustums, and it seems to work properly.

The only detail (compared to AABB test) is that one has to compute distance to all 8 points of frustum (and can't use axes for optimization) to select minPoint and maxPoint.

To the question - is my approach here correct, or am I missing some case where this test will fail?

I would just take the 8 points of the ostensibly inside frustum, generate vectors from two opposite corners of the outside frustrum, and do the 6 dot products of those vectors with the of the outside frustum plane normals. You check each point like that and if they are all on the correct side of the planes, it's inside. You can get away with only 2 corners because each corner covers 3 planes.

Vilem Otte said:
To the question - is my approach here correct, or am I missing some case where this test will fail?

It would fail if you swap the two frustums. Meaning, if you draw your red lines on the right frustum instead the left, there is no line which has all others frustum points on the outside.

I think the usual way to deal with this is to perform the test a second time with swapped inputs if needed.

I also think this helps with some typical failure cases where frustums intersect, but no other vertex is inside the current frustum.
Such cases are ‘edge crossings’ (edge intersects two other faces - a case only existing in 3D) or one frustum completely inside / outside the other.

To handle all cases, some more checks might be needed, i guess.
Usually it's not easy to think of all cases which might go wrong. But i guess time would tell, e.g. flickering shadows. But ofc. this only reveals accidentally culling, not having processed redundant work.

One alternative i can think of is to look at it like software rasterizing polyhedra.
You treat one frustum as the polyhedra to render, and clip all its faces to the other frustum representing the camera. Just like in the frustum clipping stage of a rasterizer.
If nothing survives the clip, it's outside. If everything survives, it's inside. Otherwise they intersect.
It's slower but robust without uncertainty. And maybe still faster than SAT because it utilizes the frustum property.

Gnollrunner said:
I would just take the 8 points of the ostensibly inside frustum, generate vectors from two opposite corners of the outside frustrum

I'm quickly confused. How do you tell which is ‘ostensibly inside’, why does this matter,
and how do you generate (multiple) vectors from just two points?

JoeJ said:
It would fail if you swap the two frustums. Meaning, if you draw your red lines on the right frustum instead the left, there is no line which has all others frustum points on the outside.

I think the usual way to deal with this is to perform the test a second time with swapped inputs if needed.

Yes, I think that's the part I was missing - as there is 6 planes. The original version works too - but has some false positives (as it misses additional 6 planes to test). Or at least for the test cases compared to SAT approach when I was flying with free camera around the scene.

So far - so good - no flickering shadows, and based on a “good guess (TM)" it does seem to do its job - reducing number of shadow maps to render, at least in my test - which is a sponza with spot light, point light and directional light (and atlas where every shadow was forced to same size, because otherwise it's a nightmare to read what is in it:

I'll switch to that one until the point someone complains about popping/missing shadow (or until I see those).

JoeJ said:

I'm quickly confused. How do you tell which is ‘ostensibly inside’, why does this matter,
and how do you generate (multiple) vectors from just two points?

Let me clarify this. What I meant by ostensibly inside is, the one you are checking to see if it's inside the other. Now a frustum has 6 planes and 8 points, and you want to generated vectors from the planes of the outside frustum to points of the “inside” frustum. So that's 48 vectors. However, since the planes share points at the corners you can just use two opposite corners and get 16 vectors. Now for each point of the “inside” frustrum you do 6 scalar projections (i.e. dot products). You use one of its vectors that you just generated, and the normal of the plane you are checking. Make sure to use the vector associated with that plane. So assuming your outside frustum normals point inward, you will get a positive number if a point is on the correct side of the plane to be inside. If you get 6 positive numbers the point is inside the frustum. If all 8 points of the ostensibly inside frustum are really inside, the frustum is inside since frustums are convex objects.

Gnollrunner said:
However, since the planes share points at the corners you can just use two opposite corners and get 16 vectors.

Thanks, but i'm still confused. It's hard to explain, and i would assume what you describe is the same approach Vilem has illustrated before.
But then you wouldn't reply, thus there might be some optimization i fail to spot.

It's about using just two corners. Vilem does this too, but he needs to iterate all points to find the closest and farthest to the current plane. And he needs to do this process for all planes.
Do you say that's not needed, and we can just select two random but opposite points ignoring all the others?
I mean, this would not work. You would test only a line against a frustum, so you would miss intersections.

That's where i am. Maybe you can clarify further. ; )

Vilem Otte said:
I'll switch to that one until the point someone complains about popping/missing shadow (or until I see those).

Yeah, but i'm worried about the other failure: You render some SMs which you then do not use.
Those cases will be rare, but likely an exact method is worth it to prevent them.

I was thinking about another potential optimization, which works for SMs you regenerate every frame.
Assume you record the planes of the camera frustum which intersect the SM frustum.
You could then add those camera planes as additional clipping planes for the SM render, reducing both vertex and pixel work. Iirc, APIs allow something like 16 additional custom clipping planes.

Btw, recently i've got the covariance matrix stuff to work you have shown me a while back. Calculating Eigenvectors did not work for some reason, but then i replaced this with singular value decomposition code and i got the expected results matching my former, somewhat strange method using spherical harmonics.
That's really great. I'll use this a lot. :D

JoeJ said:

That's where i am. Maybe you can clarify further. ; )

What I descried tells you if the whole frustum is inside another. If you need to do any part the frustum you can just clip successive edges against the planes until you find an edge fragment. You should do it both ways in case the “inside” frustum surrounds the other one in such a way there are no fragments in the first check. There are a bunch of simple early checks you can do of course but it doesn't seem like a complex problem, but maybe I'm missing something.

Gnollrunner said:
What I descried tells you if the whole frustum is inside another.

Ha, ok.
Agree clipping edges is enough, no need to keep forming clipped polygons as i had suggested with the rasterizing example.
Amount of dot products remains the same too, so maybe it's not so much slower either.