Hello, i've been developing my own physics engine for a couple months, and recently i have came across this issue with collision resolution.

the following image represents the problem:

As you can see, since the collisions are solved individually, the sphere get stuck on this ping pong of collisions, one possible solution would be to repeat the algorithm multiple times until the sphere is pushed out of both shapes, but i can't use that solution because it would ruin the performance of the engine, i feel like the solution would be to consider all the colliding planes at once and find the spot where the sphere could fit between the planes, as shown in the next image:

My real question here is, how can i find that plane (the one shown in red) between the contact planes which represent the smallest possible space that sphere can fit between the two planes based on the planes normal orientations and positions?

At the point of contact between the sphere and the plane, a 90 degrees orthogonal plane will go through the sphere center. If you do that for both contact points you get a symmetric (stretched rectangular) shape that is symmetric at both side above and below the plane through the circle center and the common point of the original planes. So take ½ of that rectangular shape and you have a triangle, with known length of the sphere radius side and the ½ the angle between the original planes. From that you can easily compute the length of the triangle side from the common point of the original planes to the contact point.

EDIT: Alternatively you may want to compute the length of the side between the sphere center and the common point of the original planes, as that's the distance that the sphere center must obey wrt the common point of the original plances.

The easiest way I see to calculate where the sphere could be would be to compute two new planes that offset R units from the original positions along the normals. Then, calculate the intersection line of the two planes. This line is all points where the sphere can be touching the original two planes. You can then project the sphere center onto the line to get the closest location where the sphere is touching. This would work easily with just 2 planes, but cases with more than 2 planes would be harder because there isn't necessarily an intersection line, it may be a point. The idea here is similar to inflating geometry by the sphere radius using a minkowski sum, and then treating the sphere as a point.

In practice I'd just use the collision constraint solver to do this, because it will try to satisfy the constraints for all contact points, and will converge to the desired solution. You can try an ad-hoc approach like I describe above, but it is less of a general solution.

This kind of stuff was a big pain in the ass for me. If this is for a character controller you can use sphere sweeping so you never actually enter the geometry in the first place, which makes things a tiny bit simpler. That basically reduces the response movement calculation to two collisions at most, which is the cross product of the two contacts. If you contact more than two you can consider all the pairs and take the best solution. This worked great for me, but again it starts with a different premise which doesn't apply to you if you are entering the geometry.

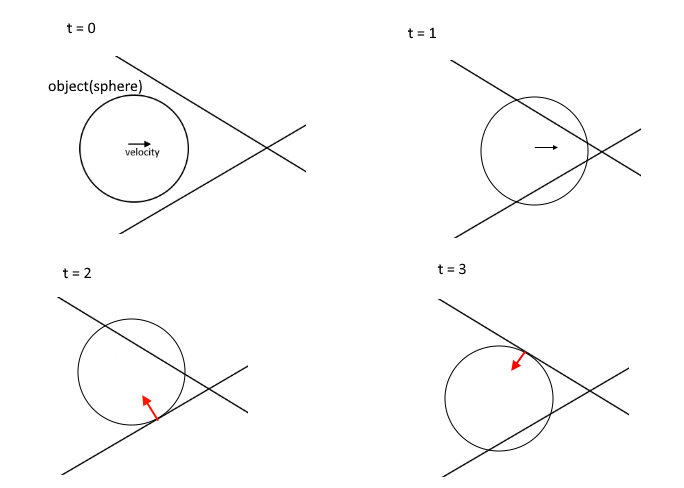
The other thing is you can't just solve a double collision since you will have more than two collisions in one time step, sooner or later (probably sooner if your geometry is anything like mine). If you contact a point where several triangles meet you can have many.

I might try this in your case……. For multiple collisions find the first collision and go back to that spot. Since it's the first, you won't be contacting anything else at that point. Then do the response for that one collision. However, you still have to consider double collisions at some point. Say you are pushing up a small valley. The first plane pushes you into the other, and other pushes you back into the first. So you are at a deadlock, which is where the cross product comes in again.

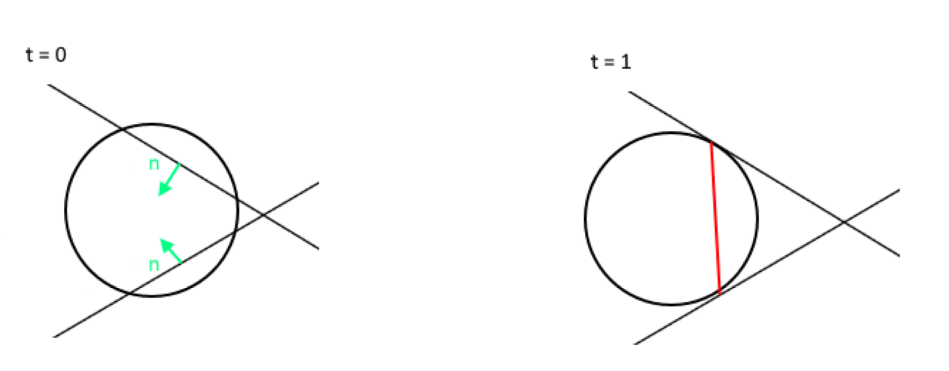
So let's say you are doing a response for a single collision, and you hit another plane. You can check at the end of the movement if you are still next to the original plane that caused the response. If so, now you can use the cross product of the planes and keep going.

There are some caveats. So say you are going down your cross product and you hit yet another plane (which can be a very common case). Now you are touching 3 planes. But you can still take the 3 pairs, calculate the cross products of those and pick the best one by comparing them to your force direction with a dot product. This is really just a generalization of the double plane case.

As I said this is what I do, and it lets me go over very random geometry without locking up.

If this is for a character controller or a physics engine, you should absolutely just iterate multiple times, each iteration pushing out of each plane one by one.

AFAIK this is how all existing physics engines do it, as well as how most character controllers do it (see eg this video: they push out of each plane repeatedly, correcting only 0.2 of the error each time, to converge in a solution to all the planes https://archive.https://archive.org/details/GDC2014Catto​

If you want some tips for how to generate the plane constraints, this paper is great: http://www.codercorner.com/MeshContacts.pdf

@popcorn000 Part of the problem is tunnelling , where the object is already penetrating (or completely passes thru if it's moving fast) a boundary in a time step dT. What I'm doing for collision detection is instead of trying to detect if a collision has occured in time step dT, I calculate the time that will be required for a collision, Tx. If Tx<dt, then a collsion has occured and needs to be handled. When I update the position of my object, I use Position+=Velocity * Tx (not dT). This will put your object at the line's edge. You may still have some time remaining if Tx<dT, and can use that extra time to calculate a ricochet position or whatever.

The trick is how to calculate the amount of time needed for a collsion to occur, if it occurs at all. For a circle and line, it's not too hard. You need to calculate the distance between the center of your circle and the closest point on your line as a function of time. Set the distance equal to the radius of your circle and solve for time. If the distance from the projection to the center of your circle is less than the radius of the circle, there's no collision.

The distance between the center of your circle (a point) and a line can be calculated using a scalar projection.

@scott8 Yes this is basically what I do and I think it's used in many video games for the collision capsule. It's called sweep sphere collision detection. However, I've been told for general physics it's slower. But it does avoid problems of fast moving objects going through relatively thin walls and so forth.

@gnollrunner In general it's Continuous Collision Detection. That's the only way you can accurately resolve collisions between objects (especially when both are moving at non-small velocities). Discrete collision detection is going to work only when objects move rather slowly in between time steps (and even then - the accuracy might hurt … this being said, discrete collision detection can be used to numerically solve continuous collision detection problem as you can oversample).

Continuous collision detections can get somewhat computationally very intensive once you get into swept tests for convex hulls.

Sweep tests aren't a complete solution to this problem, because you'll always need a tiny bit of buffer space to avoid numerical issues. (See the notes in the “Skin Factor” section of this for an explanation: https://github.com/RandyGaul/player2d​ ) This means you're going to have to deal with depenetrating from multiple planes simultaneously no matter what, it's unavoidable. Relaxation (solving the planes individually, iteratively) is the most common solution, as I mentioned before.

raigan said:

This means you're going to have to deal with depenetrating from multiple planes simultaneously no matter what, it's unavoidable. Relaxation (solving the planes individually, iteratively) is the most common solution, as I mentioned before.

I never depenetrate from any collisions. I simply don't enter the geometry. I do have a slop zone since you can end up slightly below the contact sphere due to numerical imprecision, but I never move backwards. Also as far as I know you have to consider at least two contacts for the response sometimes, since if you are in a corner the response can involve both contracts. Three contracts generally means you a stuck so you just exit.