say if I have an object at a certain position and i want to go to a certain position in another object by going around/rotating a pivot or another object.
right now, what i did is I linear interpolate the position every frame but the problem is it zooms inside the object which is not the effect I am looking,
example if the current camera position is at (0,0, -1) looking at the object at (0,0,0), then i want to go to (0,0,1) with linear interpolation, it will go thru inside the object. what i want is to rotate around that object.

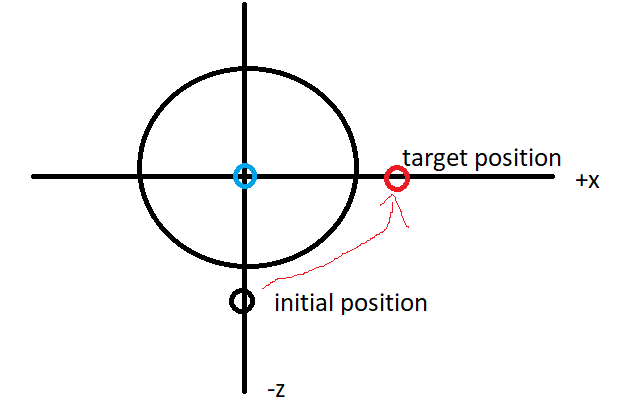
i mean situation like the above is simple to figure out
i can just rotate the point around the pivot object center position (blue) and uses (0, 1, 0) as my axis as it only rotates around the Y axis.

my problem is say the original position is somewhere with x, y and z values, that means i need to rotate it in all axis. such as this drawing

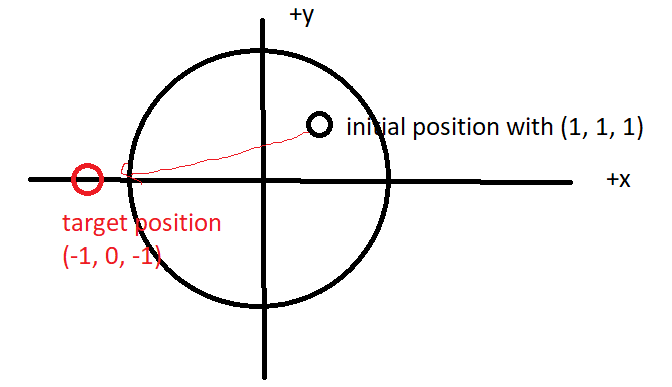
Now i need to figure out the axis to rotate to, and i am confuse on how to compute the axis to rotate to.

one idea i have is to get the difference between each axis, and use it as an angle and rotate them individualy using each axis.

angleX = targetX - origX

angleY = targetY - origY

angleZ = targetZ - origZ

new X position = rotate in axis (1,0,0) with angleX

new Y position = rotate in axis (0,1,0) with angleY

new Z position = rotate in axis (0,0,1) with angleZ

but the above results to new vector3 positions instead and kind of a bit hacky (i think).

Anyone got better or correct idea?

You can calculate a rotation axis using the cross product:

vec3 axis = normalize(cross(pointA - centerOfRotation, pointB - centerOfRotation)); 

JoeJ said:

You can calculate a rotation axis using the cross product:

vec3 axis = normalize(cross(pointA - centerOfRotation, pointB - centerOfRotation)); 

hey thanks for this, and it works somehow but, i got another problem
say if the original position is at (0, 0, 3) and the target position is at (0,0,-3) which is exactly a straight light,
center is at (0,0,0), this case cross product is at (0,0,0), which instead of rotating around the origin, goes straight forward again returning to my original issue.

any idea how to resolve this?

cebugdev2 said:
any idea how to resolve this?

If the two vectors are 180 degrees apart and form a line, there is no single plane shared by those vectors and their origin. Instead we can choose any plane containing the line, which gives us an infinite number of solutions.

So what we can do is to calculate any from those infinite solutions in a somewhat random way. For example by calculating an arbitrary tangent of the line and setting angle of rotation to 180 degrees:

	static inline const vec3 ArbitraryTangent (const vec3 &v)
	{
		float x = fabs(v[0]);
		float y = fabs(v[1]);
		float z = fabs(v[2]);
		vec3 temp;
		if (x<=y && x<=z)		temp = vec3 (1.f, 0.f, 0.f);
		else if (y<=x && y<=z)	temp = vec3 (0.f, 1.f, 0.f);
		else					temp = vec3 (0.f, 0.f, 1.f);
		temp = v.CrossProduct(temp);
		return temp.Normalize();
	}
	
	vec3 a(-1,0,0), b(1,0,0);
	vec3 axis = ArbitraryTangent (a);
	float angle = PI; // -PI would work too, so our angle is arbitrary as well

Here another example where i calculate a quaternion rotation between two vectors (two variants, depending on if they are normalized or not):

__forceinline void FromVecToVec (const sVec3 &dir0, const sVec3 &dir1)
	{
		sScalar dot = dir0.Dot(dir1);
		(*this)[3] = 1.0f + dot;
		if ((*this)[3] >= FP_EPSILON)
		{ 
			*((sVec3*)this) = dir0.Cross(dir1);
			Normalize();
		}
		else
		{
			if (dot<0) *this = sQuat (0, 0, 1.0f, 0); // 180 degrees apart -> 180 degrees rotation around z
			else *this = sQuat (0, 0, 0, 1.0f); // 0 degrees apart -> zero rotation
		}
	}
	__forceinline void FromVecToVecNonUniformLength (const sVec3 &dir0, const sVec3 &dir1)
	{
		sScalar dot = dir0.Dot(dir1);
		(*this)[3] = sqrtf(dir0.SqL() * dir1.SqL()) + dot;
		if ((*this)[3] >= FP_EPSILON)
		{ 
			*((sVec3*)this) = dir0.Cross(dir1);
			Normalize();
		}
		else
		{
			if (dot<0) *this = sQuat (0, 0, 1.0f, 0); // 180 degrees apart -> 180 degrees rotation around z
			else *this = sQuat (0, 0, 0, 1.0f); // 0 degrees apart -> zero rotation
		}
	} 

The code is really hard to read. It's member functions of quaternion class using xyzw convention, so i can cast the quaternion to a vec3 to access it's xyz numbers, while i access the w number with (*this)[3].
SqL(x) gives the squared magnitude of a vector, so the same as dot(x,x). FP_EPSILON is 1.0e-6f for me.

You can see it deals with the special cases of 0 and 180 degrees in the else scope.
Usually this works for me and i almost never need to handle special cases beside that.

The quaternion formulation also shows us optimized code.
Compare all your code of axis and angle rotation construction and dealing with special cases. You'll likely end up with much more transcendental math functions, branches, and redundant code.

JoeJ said:

cebugdev2 said:
any idea how to resolve this?

If the two vectors are 180 degrees apart and form a line, there is no single plane shared by those vectors and their origin. Instead we can choose any plane containing the line, which gives us an infinite number of solutions.

So what we can do is to calculate any from those infinite solutions in a somewhat random way. For example by calculating an arbitrary tangent of the line and setting angle of rotation to 180 degrees:

	static inline const vec3 ArbitraryTangent (const vec3 &v)
	{
		float x = fabs(v[0]);
		float y = fabs(v[1]);
		float z = fabs(v[2]);
		vec3 temp;
		if (x<=y && x<=z)		temp = vec3 (1.f, 0.f, 0.f);
		else if (y<=x && y<=z)	temp = vec3 (0.f, 1.f, 0.f);
		else					temp = vec3 (0.f, 0.f, 1.f);
		temp = v.CrossProduct(temp);
		return temp.Normalize();
	}
	
	vec3 a(-1,0,0), b(1,0,0);
	vec3 axis = ArbitraryTangent (a);
	float angle = PI; // -PI would work too, so our angle is arbitrary as well

Here another example where i calculate a quaternion rotation between two vectors (two variants, depending on if they are normalized or not):

__forceinline void FromVecToVec (const sVec3 &dir0, const sVec3 &dir1)
	{
		sScalar dot = dir0.Dot(dir1);
		(*this)[3] = 1.0f + dot;
		if ((*this)[3] >= FP_EPSILON)
		{ 
			*((sVec3*)this) = dir0.Cross(dir1);
			Normalize();
		}
		else
		{
			if (dot<0) *this = sQuat (0, 0, 1.0f, 0); // 180 degrees apart -> 180 degrees rotation around z
			else *this = sQuat (0, 0, 0, 1.0f); // 0 degrees apart -> zero rotation
		}
	}
	__forceinline void FromVecToVecNonUniformLength (const sVec3 &dir0, const sVec3 &dir1)
	{
		sScalar dot = dir0.Dot(dir1);
		(*this)[3] = sqrtf(dir0.SqL() * dir1.SqL()) + dot;
		if ((*this)[3] >= FP_EPSILON)
		{ 
			*((sVec3*)this) = dir0.Cross(dir1);
			Normalize();
		}
		else
		{
			if (dot<0) *this = sQuat (0, 0, 1.0f, 0); // 180 degrees apart -> 180 degrees rotation around z
			else *this = sQuat (0, 0, 0, 1.0f); // 0 degrees apart -> zero rotation
		}
	} 

The code is really hard to read. It's member functions of quaternion class using xyzw convention, so i can cast the quaternion to a vec3 to access it's xyz numbers, while i access the w number with (*this)[3].
SqL(x) gives the squared magnitude of a vector, so the same as dot(x,x). FP_EPSILON is 1.0e-6f for me.

You can see it deals with the special cases of 0 and 180 degrees in the else scope.
Usually this works for me and i almost never need to handle special cases beside that.

The quaternion formulation also shows us optimized code.
Compare all your code of axis and angle rotation construction and dealing with special cases. You'll likely end up with much more transcendental math functions, branches, and redundant code.

this is why i love posting and asking questions here! thank you very much!