JoeJ said:
But that's because we are too stupid to implement proper iterative solutions :D

I would argue that it's because iteration requires repetition of execution, which, intuitively, feels inefficient. :P

(And perhaps I like it less than other approaches.)

JoeJ said:
Yeah, i see i'm pretty fit already again.

Ah, I'm glad that you're already improving, it would seem! ^_^

But sorry to hear about your wife having caught it, too, and about her having to work in such a state--both for her sake and that of her customers! :/

JoeJ said:
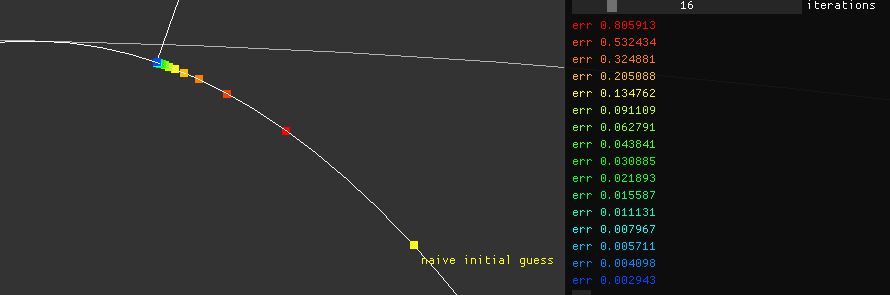
I had an idea to improve it with a better initial guess. Edited the code. Much better, but the problem remains in cases, but it's smaller.

I'm glad to read it! ^_^

I could not accept my failure and kept improving.
I noticed the problem increases the closer we get to the vertical axis, so i used that instead a damping constant.
It's pretty good now, even in a hard case like this, it nicely converges:

Though, to make the printed error zero, i'd need 42 iterations. It would need more work to map the error better.
So it surely is no great solution, but i found no cases where it does not work.

My improvement form before turned out a case of ‘make it seemingly better by making it actually worse’.
I'll completely replace the code from upper post - too much changes to mention them all.

I could not accept a working but slow solution.

Now it's really good, and i can recommend using it. I think 4 iterations are enough in any case, which was may goal. :D

Instead projecting to ellipse tangent line, i constructed a inner circle at the intersection of ellipse normal and up vector. It's neat. No magic constants, no damping, no thresholds.

I'm happy, and guess it's not much worse than Eberlys maybe, which i still should take a look at now…

Eberlys paper has even code.
And the code looks faster than mine, i'd guess something like 5-10x faster.
But he also states, for floats, his maximum iteration count is 149.

So i did this for a comparison, of which i don't know how fair it is:

					float move = vec2(ellipsePoint - oldEllipsePoint).Length(); // travelled distance withi current iteration
					ImGui::TextColored(ImVec4(R,G,B,1), "move %f", move);
					if (move < std::numeric_limits<float>::epsilon())
						break;				

It shows i need only 6 iterations in difficult cases to reach precision limits.

Thus i may even win over Eberlys method? How cool is that?

Or just Blasphemy? I'd reference him. He was here, but can't find his username.

JoeJ said:
Thus i may even win over Eberlys method? How cool is that?

Well done one doing that, I'd say! ^_^

If (and as far as) I understand your method correctly, it does seem pretty good, and should produce good results, I imagine!

As for my own approach, I think that I have a workable method for the case in which the point lies above or below the unsquashed circle--but currently only if it also doesn't lie beyond the left or right extent of said circle…

(In short, I'm still using the difference between the squashed and unsquashed circles, but in this new case I'm using the vertical instead of horizontal position of the test-point to find the relevant widths. But that doesn't help if the test-point is then also beyond the horizontal bounds of the circle, leaving the vertical position no longer mapping to any point on the circle…)

I'm tempted to just clamp the test-point's vertical position in the “width-difference” step such that, below and above the circle, it always ends up at the bottom and top of the circle, respectively. That might be good enough for my purposes, if not quite satisfying…

Thaumaturge said:
If (and as far as) I understand your method correctly, it does seem pretty good, and should produce good results, I imagine!

This is how it works:

You can model an ellipse with circles along it's major axis.
So i get an approximate close point, construct the circle touching that point, calculate exact closest point on the circle, project it to the ellipse and proceed.
The projection errors reduce quickly, so it's fast, and i don't see any failure cases. (Though i have not worked out special cases causing divisions by zero, for example)

Problem with the former method of projecting the query point to the tangent was that this projection was often far away from the current guess on the ellipse, causing oscillations.
With the circles this can't happen because they are not infinite, opposed to a tangent.

Eberlys method surely is more elegant, as he probably constructs a equation to minimize distance, then working on just that ignoring geometry. The iterations are just 5 lines of code of root finding without a need to access memory.
And i guess it works well with much less than 150 iterations, so i really don't know which is faster. Accuracy is probably the same.

JoeJ said:
This is how it works:

…

Okay, yes, I believe that I understand now. Thank you for the explanation! ^_^

Update on my method: I believe that I've managed to reduce the issues that it has to a tolerable level, and indeed, have it working in my project. ^_^

In short, when the player's position lies below or above the circle, I perform a similar process to that previously-described (finding the difference between the width of the squashed and unsquashed circles), but making use of the player's x-coordinate to determine the relevant points on the circle.

Since this gives results slightly different to those of the vertically-interior case, I then interpolate between the two based on the player's x-coordinate. (This still being confined to the case in which the player is above or below the circles, to be clear.)

Furthermore, the player's x- and y- coordinates are clamped for the purposes of this process.

The results aren't perfect, but thus far they seem to be acceptable for my purposes. ^_^