I'm led to believe that there are chaotic trajectories with regard to the Mandelbrot set. Does anyone have experience with this? Am I even making sense?
Pretty picture….
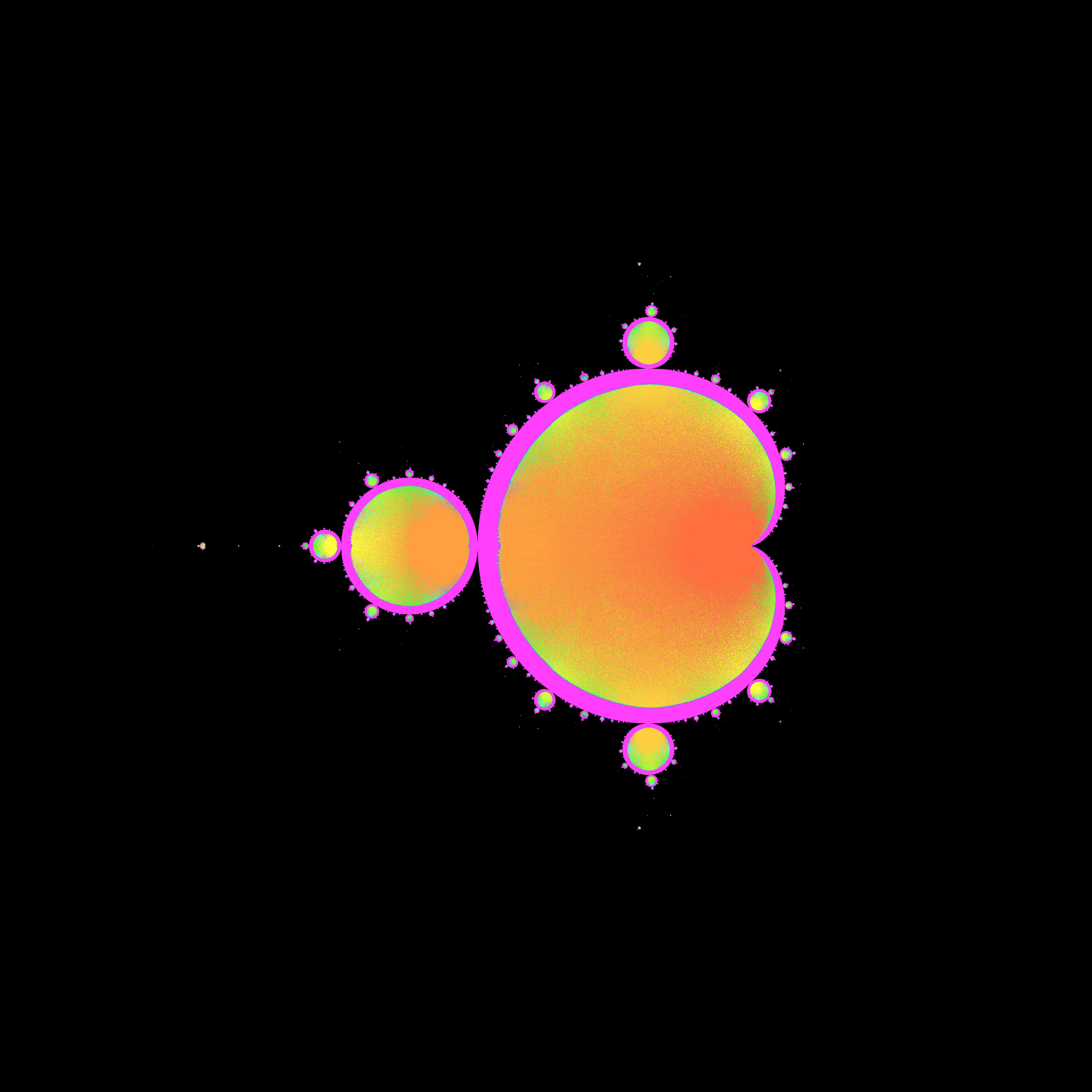
I'm led to believe that there are chaotic trajectories with regard to the Mandelbrot set. Does anyone have experience with this? Am I even making sense?
Pretty picture….

taby said:
I'm led to believe that there are chaotic trajectories with regard to the Mandelbrot set. Does anyone have experience with this? Am I even making sense?
Interpreting ‘chaortic’ naively, i would say yes.
You know i did those experiments, focusing on just a single pixel of the Mandelbrot set. Visualizing the complex number z, we sometimes get nice spirals around on integer number of convergence points (likely so at pixels which do not escape quickly):
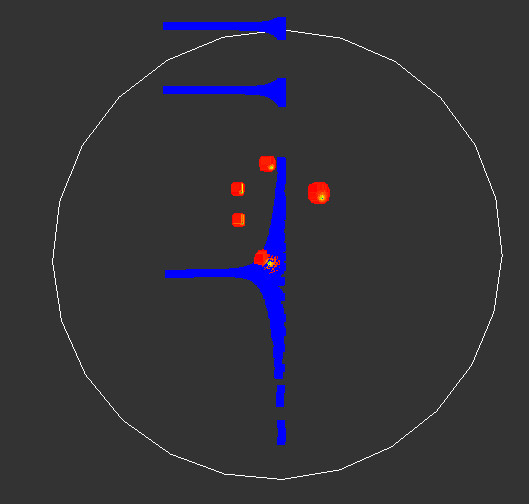
White circle is escape radius. No idea what i had shown with those blue plots, but seems related to these points.
So we see a pattern and no chaos.
Then, looking at another pixel, which does escape quickly, it looks like chaos:
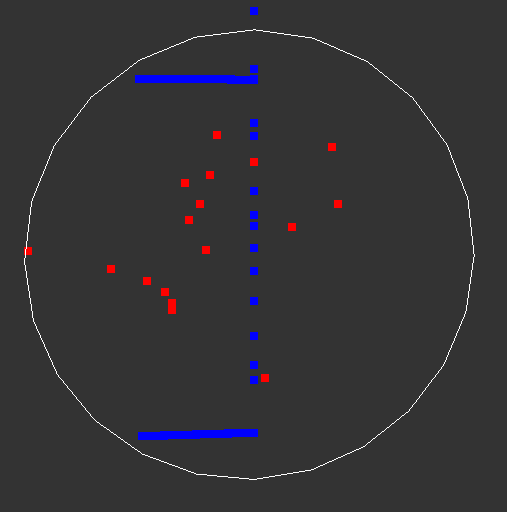
Would be better to draw lines between the points to relate this to a trajectory.
If we did this, we would see in the above spirals image, that points are added to one galaxy after another. Ofc. it does not draw one whole galaxy and begins to draw the next.
Which illustrates the rotation happening in z = z*z + c with the multiplication, while the addition is a translation.
Not sure if this at all is related to your question ; )
Btw, i tried distance estimate for the MandelBox fractal, as discussed last time. The geniuses at fractalforums did post some formulas.
But sadly it only gives distance outside of the set. I would need surface distance from the inside too. Seems i need to figure this out myself…
Thanks for your input JoeJ.
I think that I might have found what I'm looking for. I get an acyclical trajectory when I use any of the following four input locations:
-1, -0.25
-1, 0.25
0.25, -0.5
0.25, 0.5
The following is a diagram of these four trajectories. Are these chaotic?
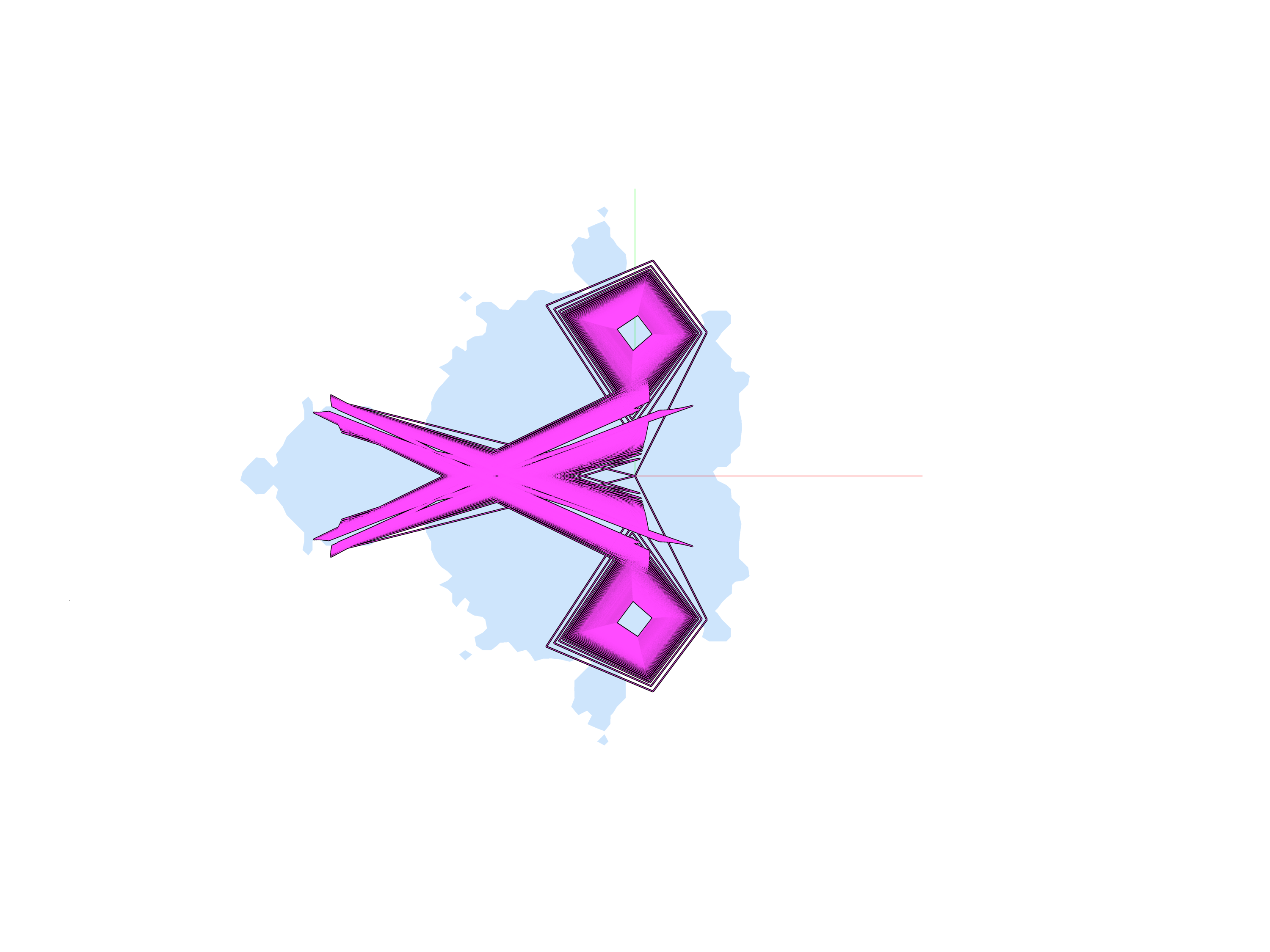
In general, any one trajectory cannot be chaotic, because it is deterministic.
The general classification of a “chaotic” system or function is that a small change in input has a nondeterministic, full-range possible change in output. The simplest chaotic system is the three-body (gravity in space) problem.
The function of “what trajectory do I get, when I follow a point around in the Mandelbrot set?” is chaotic, because a small change in input point may return a full-magnitude, unpredictable change in what trajectory you get, but a single one of those is not “chaotic” in itself – it's just a single part of a larger chaotic system.
Separately: For the points that don't escape, they generate infinite cycles. The full plot of all those cycles is what makes up the Julia set for the Mandelbrot function for a given starting point, and is typically what people draw when they say they plot “the Julia set” (although the Julia set is really a higher-order function generating a set on a function.)
It's maybe related to the logisitc map, which can be mapped to the mandelbrot set and also has such chaotic and ordered sequences: https://en.wikipedia.org/wiki/Logistic_map
Hey, somebody told me to try calculating the Lyapunov exponent. I have no idea where to start.
When you have a math question, try MathWorld first, and if that doesn't work, check Wikipedia.
https://mathworld.wolfram.com/LyapunovCharacteristicExponent.html
AFAIK, chaos is always deterministic. I wrote a deterministic (pseudorandom) number generator once:
https://vixra.org/pdf/1202.0094v3.pdf