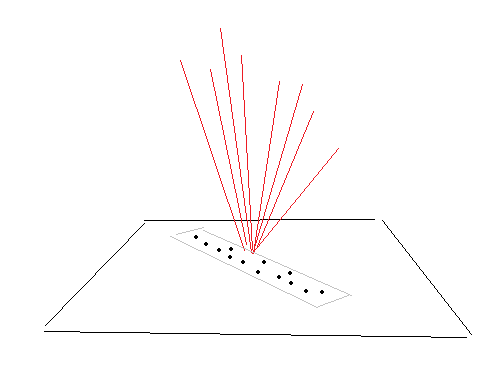
I have a bunch of normals all within a cone - at the moment I am compressing the normals individually, so Im not making use of the fact that the angle between any normal and the cone axis is less than a certain amount,

Each normal consists of three floats (IEEE754 32 bit ). Although the compression I outline below works well for general normals, The fact that they all lie in a cone would imply that I should be able to compress better… any ideas here ??

Current compression:

Take the absolute biggest scalar component of the normal, call it ‘b’, which will be in the range [1/root(3), 1]. Scales to the closed/open range [1, 2) so that the sign and exponent are constant and then storing only the mantissa (as many bits as required) and the sign of the component. The second biggest (absolute) will be in range [ root( (1 - b^2) / 2 ), root(1 - b^2) ] - so similarly scale to [1, 2) etc. The third element can be trivially calculated from the first two on decomopression ie. +-sqrt(1 - b^2 - c"2). Note: when scaling to the range [1, 2) care needs to be taken with fpt rounding etc. as the maximum value should be the floating point value corresponding to bit pattern: 0x3fffffff, which is the biggest value less than 2. When decompressing the two mantissas the bit patterns are ‘OR’d' with 0x3f800000 to get [1.2) and then scaled back to the original range. ( I have code for this, too much for here but I can post snippets….)

If your normal vectors have unit length, you should be able to reconstruct normals from two angles instead of three vector components using the usual spherical coordinates, dropping one degree of freedom due to unit length.

There should be an implicit, “natural” direction to form a reference frame with the cone axis. What is it? What are your cones and your normals? Maybe further assumptions and specializations are possible.

MrPotato said:
The fact that they all lie in a cone would imply that I should be able to compress better… any ideas here ??

Using the cone direction as a plane, you could parametrize the normals to a 2D rectangle on that (requiring no trig). Storing the bounding rectangle of all normals on this plane would be necessary to minimize error. So if cone angles are small, i can imagine 16 bit per normal could work good enough. If your normal distributions per cone are often anisotropic, it might be worth to find the optimal orientation of the rectangle on the plane es well, increasing accuracy but then requiring an additional tangent per cone to store.

LorenzoGatti - Thinking about this - yes, spherical coordinates. just need to work out the angle ranges given a normal (the axis of a cone) and internal angle of this cone. Ill try this at weekend.

JoeJ - Projecting normals to the plane and min/max bounds ? - I'm thinking that finding the optimal plane for this might be some kind of eigenvector solution…. Going to try some ideas at weekend, thanks.

MrPotato said:
JoeJ - Projecting normals to the plane and min/max bounds ? - I'm thinking that finding the optimal plane for this might be some kind of eigenvector solution…. Going to try some ideas at weekend, thanks.

I think the optimal plane normal should be very close to the average of all normal vectors, but IDK if eigenvectors could help to optimize this further.

The harder problem is to find the best orientation of the rectangle on that plane, which is the same problem as finding a line to approximate a set of points in 2D. What i prefer here is to raise complex numbers to the power of 2, sum them up, finally convert back the result by raising to power of 0.5. This gives exact result in O(n) and works much better for me than least squares regression.

After that, you could say to use 4 bits for the shorter side, and 12 bits for the longer side of the rectangle. But it depends on your data if this idea makes sense ofc.