Hello, I am working on a VR game where the player does not have 1:1 control over their hands. Instead, the VR controllers act as a goal that the in-game hands will interpolate towards. (For the curious—this is the game.) Currently, we are using linear interpolation. This works will for when the goal is travelling in a straight line, but when it arcs (which is very often, since our arms primarily move in arcs), the hands will take a shortcut. This is undesirable for our gameplay, as it often makes players feel their arms are shorter than they are.

https://gfycat.com/indolentwelloffcaiman​

An improvement over this is to follow the goal by storing a list of its positions over time.

https://gfycat.com/astonishingqueasybarebirdbat​

This works very well for standard arcing motion, as seen in the first half. However, in the second half we can see that following the goal exactly causes the hands to zig-zag as they approach the goal—this is also undesirable behaviour.

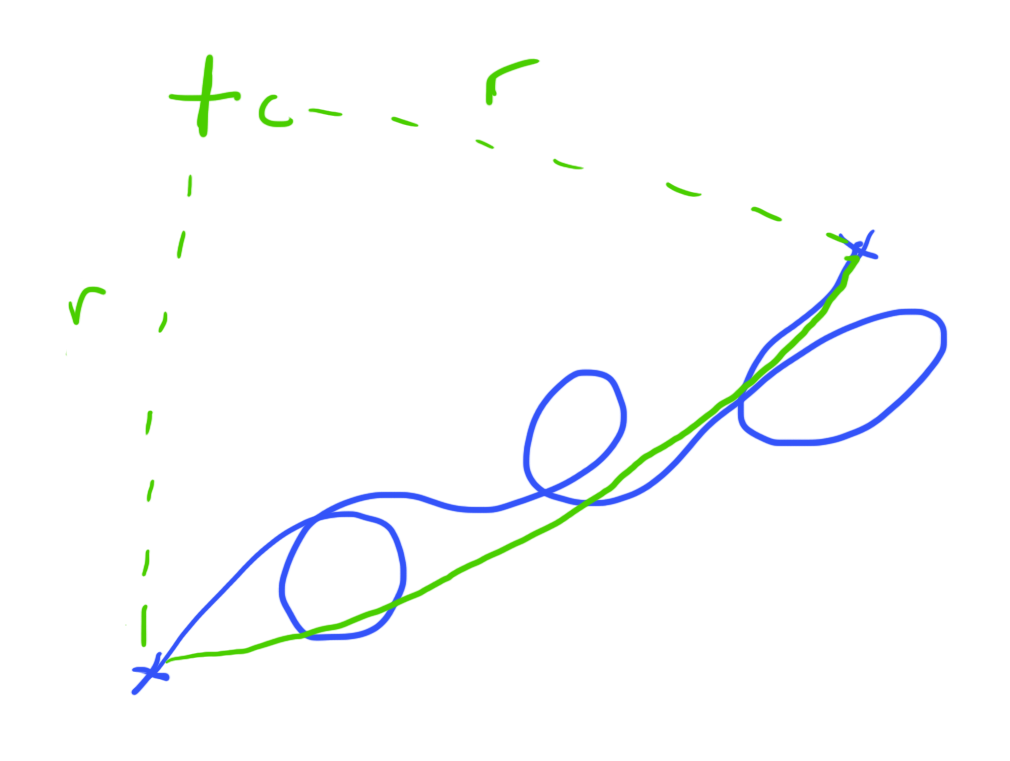
To solve this problem, I am looking for a curve fitting algorithm that, given the blue curves below (represented as lists of positions) would produce something similar to the green curves.

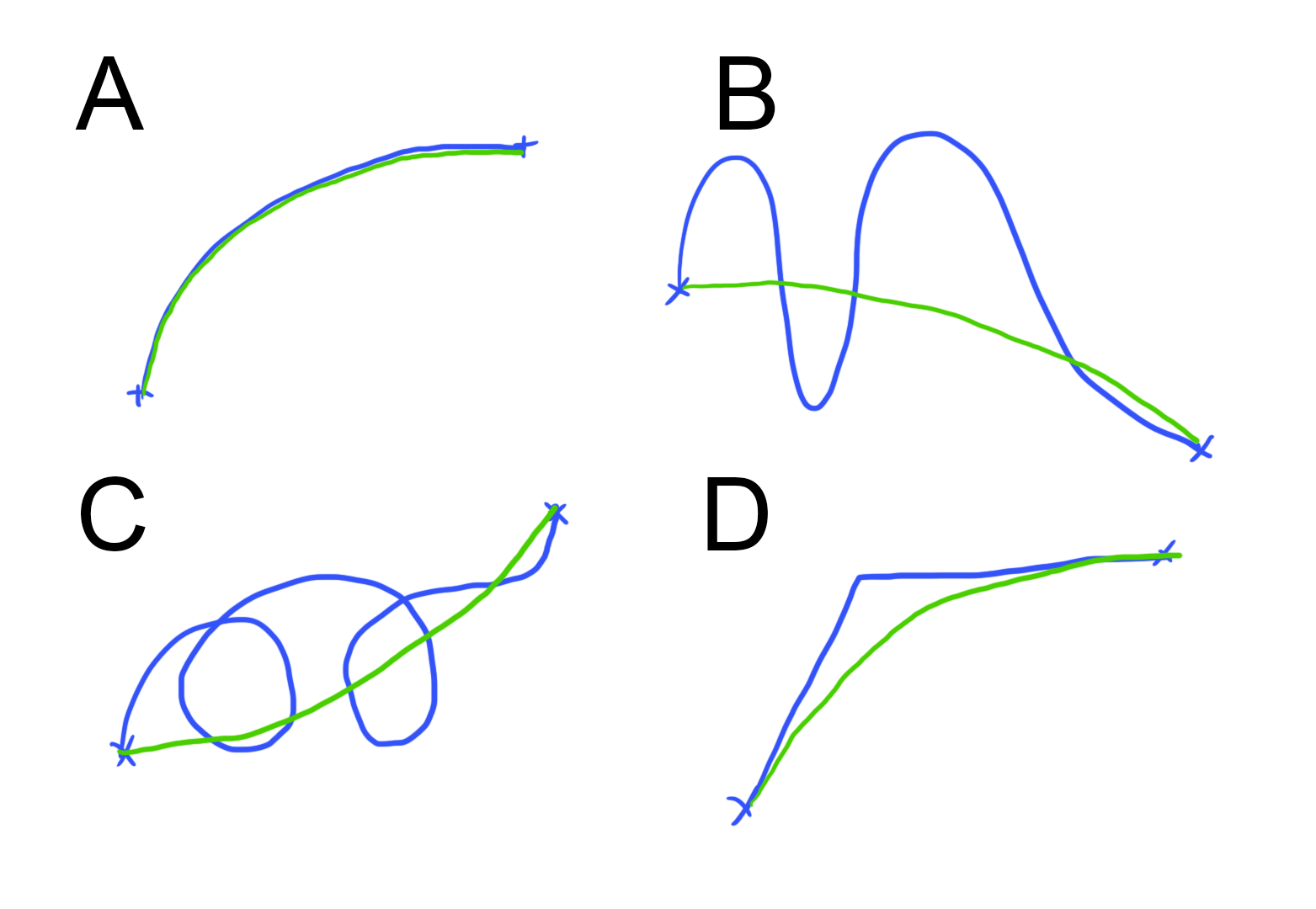
The requirements I'm thinking are that the output curve would

1. Attempt to fit the input curve, but the angle between adjacent points would never be allowed to be greater than some constant (as we can see in A and D). I did a rough pass on this where I trim any edges that do not satisfy this requirement.
2. Not be allowed to “double back” on itself, as seen in B and C.

^^2 is the one I am struggling with. I am searching for a curve fitting algorithm that would somewhat fit (ha) these requirements. I am not concerned with performance, as for the foreseeable future there will only be two objects in the world (the hands) running this code.

Thanks for any replies!

Did some research, and it seems like one promising approach would be to fit an arc (part of a circle) to the points, with an example below.

This arc would have the following constraints

1. It must begin and end at the first and final points from the inputs.
2. It must have a radius greater than some arbitrary k (by setting k to reflect the radii of arcs we naturally produce with arm motions, we would avoid creating tiny little loops from noise).
3. It should fit the input points well.

This article outlines how to transform the problem from 3D space to 2D, as well as how to fit a circle to them using least squares. Getting the first two constraints to match may be tough, but there's always guess and check to fall back on.

Using an arc like this fits all the requirements above, provided the arc stays stable between frames (each frame the hand would consume some points and the goal would produce a new one). Will have to read up a bit more and try it out, but if anyone has run into anything like this before feedback is always appreciated.

EDIT: Did the above, got pretty good results. Next step is to get it in 3D and see if it holds up to real user interactions.

https://gfycat.com/flickeringunsungelectriceel

Not following zig-zag motion is impossible because it would require precognition: the follower doesn't know whether the leader will zig-zag back in the future, or whether it really means to go sideways.

For example, consider your diagram D. The reference could stop at the corner instead of continuing with the second straight segment, and in this case the correct trajectory for the follower would be straight, exactly following the reference.
But the follower must choose a direction as soon as it starts moving and it has no reason to think that the reference will suddenly turn right and that it should anticipate that turn with the appropriate degree of smoothing seen in the diagram.

In any feasible scheme the follower can only begin turning after the reference turns, and the first part of example D can only be a straight line.