Hey,
I have a set of loose point masses. I integrate velocities like this:
for (int i = 0; i < pointMasses.Length; i++)
pointMasses[i].velocity += pointMasses[i].force * dt / pointMasses[i].mass;I thought about making an experiment. I took 4 points masses and positioned them such that they compose a box. I wanted to use rigidbody formulas to make the “rigidbody” rotate correctly, i.e. determine point masses's points such that after integration they still maintain distances between each other unchanged + angles.
The basic formula for velocity of a moving point (Q) relative to rigidbody's center of mass (P) is this:
Q_v = P_v + W x (Q - P)
Q_v - velocity of Q
P_v - linear velocity of rigidbody (or center of mass)
W - angular velocity of rigibodyCode (in C#) that does integration looks like this:
Inputs are:
- pointMasses - list of point masses
- force
- pointOfForceApplication - set to one of the pointMasses
========
float dt = Time.fixedDeltaTime;
Vector3 avgPos = [...];
Vector3 avgVel = [...];
Vector3 angMomentum = Vector3.zero;
Matrix4x4 inertia = Matrix4x4.identity;
{
float xx = 0.0f;
float yy = 0.0f;
float zz = 0.0f;
float xy = 0.0f;
float xz = 0.0f;
float yz = 0.0f;
for (int i = 0; i < pointMasses.Length; i++)
{
float m = 1.0f;
Vector3 r = pointMasses[i].position - avgPos;
Vector3 v = pointMasses[i].velocity;
angMomentum += Vector3.Cross(r, m * v);
xx += (r.y * r.y + r.z * r.z) * m;
yy += (r.x * r.x + r.z * r.z) * m;
zz += (r.x * r.x + r.y * r.y) * m;
xy += (r.x * r.y) * m;
xz += (r.x * r.z) * m;
yz += (r.y * r.z) * m;
}
inertia.m00 = xx;
inertia.m01 = -xy;
inertia.m02 = -xz;
inertia.m10 = -xy;
inertia.m11 = yy;
inertia.m12 = -yz;
inertia.m20 = -xz;
inertia.m21 = -yz;
inertia.m22 = zz;
inertia = inertia.inverse;
}
// get new linear velocity
Vector3 linVel = avgVel + force * dt / 4.0f; // 4 point masses each with mass 1.0
// get new angular velocity
Vector3 pf = pointOfForceApplication - avgPos;
Vector3 torque = Vector3.Cross(pf, force);
Vector3 angAcc = inertia.MultiplyVector(torque);
Vector3 angVel = inertia.MultiplyVector(angMomentum);
angVel += angAcc * dt;
for (int i = 0; i < pointMasses.Length; i++)
{
Vector3 r = pointMasses[i].position - avgPos;
pointMasses[i].velocity = linVel + Vector3.Cross(angVel, r);
}The problem
The problem that I have is that as the point masses set keeps rotating the object becomes “bigger”. I am using a simple 2D box (I am using full 3D formulas though) to keep things as simple as possible. I apply force to one of the vertices of the box.
Have a look at this screenshot:

It shows the initial state. I apply force to the bolded point. After a few seconds of rotation (just angular velocity, I removed linear velocity to make the box stay in one place) this is what I get:
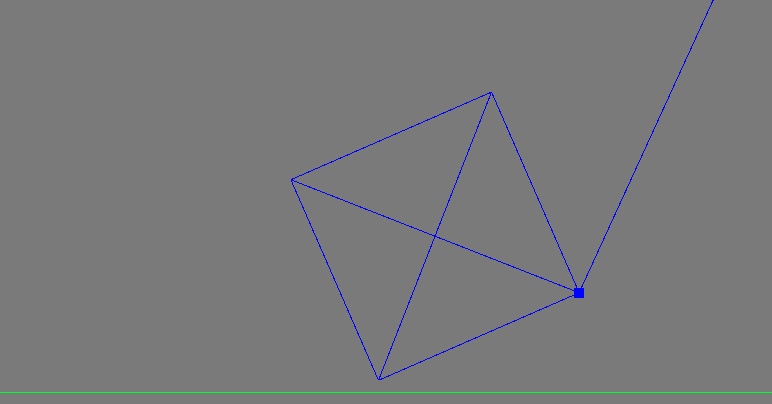
(The long line shows the direction of angular velocity of the bolded point).
Does anyone know why would the box grow bigger as it keeps rotating?