Calin said:
How do I apply a matrix to a vertex position?

http://www.directxtutorial.com/Lesson.aspx?lessonid=9-4-5
 

http://www.directxtutorial.com/Lesson.aspx?lessonid=9-4-5

how cute, reading

[edit] it was a good read, a brush up on stuff I have forgoten. It doesn`t answer my question however. I want to know the math behind matrices. ( I`m not using SetTransform() calls ). How do I get the new vertex position without calling SetTransform() ?

https://www.youtube.com/watch?v=brQZPjiwtRE

Calin said:
I want to know the math behind matrices.

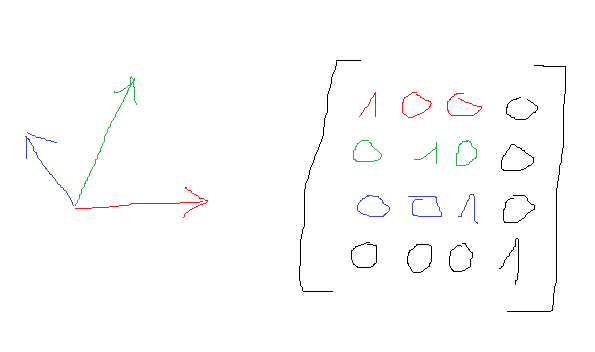
You can understand it in a geometric way, ignoring it is linear algebra. Worked well for me.

On the left we have a transform or frame, like it looks in a 3D modeling program. Red = X axis, Green = Y, Blue = Z.

On the right is the 4x4 Mmatrix with their numbers. Colored upper left is a 3x3 matrix, which we can use if we only care about rotation. 
The three axis are row vectors, colored accordingly. If there is no scale or sheer, those 3 vectors are unit length and orthogonal to each other. You can use them directly, e.g. to display the arrows on the left, but also for more useful things.

The 4th row stores position. (0,0,0) in our case. The right column (0,0,0,1) can be ignored for now (and indeed we often only store a 3x4 transform to save space and avoid useless operations).

Now an example. Assume we have a matrix for a object, and we want to transform a mesh vertex from the objects local space to the world space so we can display, or check collisions etc.
This is quite simple:

vec3 worldSpacePosition = matrix[3] + // position of object 
	matrix[0] * localVertex.x + // vertex x times orientation x axis of object
	matrix[1] * localVertex.y + 
	matrix[2] * localVertex.z;
	

(assuming i can access matrix rows with [] operater, which is usually implemented this way.)

Next example is to do the opposite. We know world position of a point and want to calculate the local position relative to the object.
 

localPosition.x = matrix[0].dot(worldPos - matrix[3]); // first move the position to the origin of the object by subtracting object position,
localPosition.y = matrix[1].dot(worldPos - matrix[3]); // then for each axis see how far the point is away from athe plane of this axis.
localPosition.z = matrix[2].dot(worldPos - matrix[3]);

Do you know how dot product works?
It's essential. if we have a unit vector like a normal, this normal has a plane (the surface it points way from). Using dot product we can measure distance to this plane.
Be sure to understand this. It's not obvious at first but easy. 
If you don't know learn about dot (and cross) product first.

Now you have learned many things:

Rotating vectors. First example did rotate by the matrix, second example did unrotate.

Because matrices are just bunch of vectors, you could now also transform a child bone matrix by the parent bone matrix. Just do above examples for each axis vector and also position.
This also implies that matrix multiplication can be understood by understanding dot product. And if you look up your matrix library multiplication code it is equivalent to doing dot products.

The 'unrotation' or ‘untransform’ is related to taking the inverse of a matrix, which also can be done with simple dot products if it is a orthogonal frame like mostly.

This is usually enough to know about matrices representing transforms. But there are pitfalls:

Conventions:

Row- and Column-major order. Some people prefer to put axis and position into columns not rows. The matrix is then transposed in comparison to my example. DirectX is an example for this.
You can still do the same things, and they often work regardless. But it causes confusion and some trial and error.

Left Handed vs. Right Handed coordinate systems. Some people have Y up, some down, for example.
 

An often used alternative for 4x4 matrix transform is using a vec3 for position and a quaternion for orientation. (Some math gurus even use dual quaternion for both)

This takes less space, but it can not represent scale.

I usually prefer it, especially when working on character hierarchies and related IK and physics tasks.

so the arrows are vectors, I got it

Yeah, the drawn axis arrows are directions, so vectors, and each is stored directly also in matrix form.

The position of the object is a point, also stored (4th. row or column - depending on convention).

So this hopefully demystifies transformation matrices, and you see how all those numbers make sense geometrically, and how they can be used e.g. to get front facing direction of a camera matrix and so on.

BTW, the difference between point and vector can be more than just rhetorical when working with matrices.
E.g.:

vec4 normal (5,0,0,0); // this is a direction, so set 4th number to 0.
vec4 transormedNormal = matrix * normal. // this performs only rotation because the 0 cancels out translation row

vec4 position (5,0,0,1); // this is a point, so set 4th number to 1.
vec4 transformedPosition = matrix * position. // performs rotation and translation

While this is nice maybe, it can waste space and useless instructions for the pure rotation, so matrix libraries often have rotation only functions so there is no need for a 4th number in the vector.

Thinking about the difference between points and vector can sometimes help in general.

It certainly helps a lot to make a difference between rotation and orientation, because that's much harder to understand and deal with.

@JoeJ Now you have to explain to me tensors.

‘Tensor’… no idea what it means. Reading it up on Wikipedia i see it is something we use a lot, but lacking math education i do not know what concepts the word really represents. Sounds like meaning pretty any mathematical construct (a single number, a complex number, a vector, also more of those for n dimensions), that can be related to adjacent constructs of the same type with a linear equation? I wish i knew better… like often : )

@JoeJ I read too, but can not understand what people do with tensors in computer science.
You give me 100 tensors…. and what next? What should i do with your 100 tensors?

When i am complete zero at something i need to read a whole e-book. Preferably with the word "dummies" in the name of the book hahaha

Definitively a book is a lot of help. Bugs never give me time to read a book.