I've decided to implement my own algorithm for optimal reciprocal collision avoidance. It doesn't use linear programming, but iteratively projects velocity on intersections of ORCA lines and checks if it is collision-free. It works great for relatively slow units, but fast units tend to stop under certain circumstances.
The problem arises when there are two or more obstacles with the same velocity, and their velocity obstacles are intersecting with each other, and the goal velocity is inside the both velocity obstacles, and the goal velocity is close to the edges of both of the velocity obstacles rather than the truncated parts.
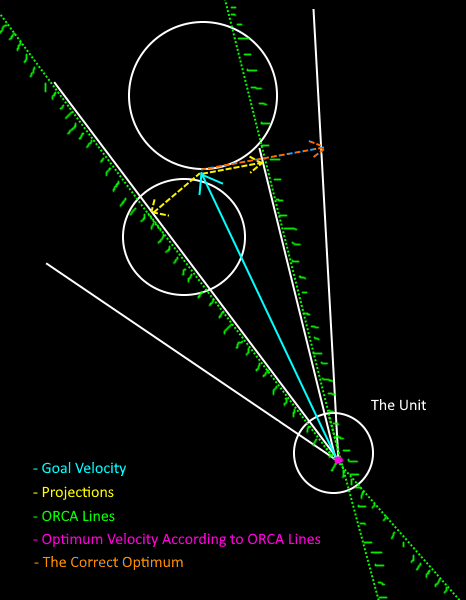
So, according to the ORCA lines, the closest collision-free velocity sometimes becomes not optimal, or locally optimal, which can cause a unit to slow down or go backward or even stop (when obstacles have zero velocity) while there actually exists a better collision-free velocity but is left out due to ORCA lines.
- I've read some papers, but none of them mentioned such problem.
- I've also tried to inspect the library which the original algorithm resides, but I was unable to understand it.
- I've tried merging obstacles into single bounding obstacle, which worked when the problematic obstacles were only two, but when there were more of them, it caused a very big obstacle, which blocked the whole way the agent was supposed to use.
If anyone is familiar with the concept and can let me know how to deal with the issue, or if anyone has another idea, I'll be glad.
By the way, the actual problem is in 3D, but I don't think it makes any difference. And I used 2 as constant T value for truncation of cones, but different values couldn't solve the problem either. Here's a picture, summarizing the problem, the obstacles are standing enemy units in this case: