Very similar. Here's the comparable figure from my 1998 patent on spring-damper physics for ragdolls. Expired this year. The paper from Valve is from GDC 2015.
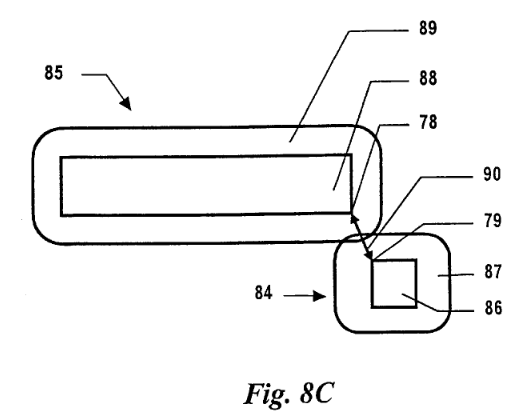
"Skin" and "Bone" contact model.
The rectangular collision objects 86-88 are rigid and are not allowed to interpenetrate. The visual geometry is out at the curved boundaries. With this approach, the closest-points vector 78-79 moves smoothly as two objects come close near a corner. If you use interpenetration and compute the collision as "shortest move to out of collision", the contact vector snaps sharply as a contact reaches a corner. In a system where the time step is variable (simulation and animation rather than real-time games) the integrator keeps cutting the time step to reduce error, trying to zero on where things suddenly changed. Timesteps can drop into the nanoseconds chasing that discontinuity. Don't want that. That's step one to smooth collisions.
Step two is multiple contact points. That takes care of what's called static indeterminacy, which is why a table with four legs not exactly the same length wobbles on a hard surface. You need some minimal springiness or error tolerance to get anything with more than three contact points to settle.
With both of these, contacts become differentiable. A tiny move will not produce a big change in forces. Now you can integrate stably.
This was for a spring-damper system. Those are more accurate, but slower. Games use impulse-constraint systems, which can be solved in constant time, but always look a little off, because there are big velocity changes in one frame time. Real-world large objects don't do that.
With enough compute power, spring-damper physics might come back. It's like ray-tracing - better, but expensive.








