My take on the questions:
First, 2D and 3D are different dimensionality. If you are making the shift from 3D to 2D, some of the concepts shift as well. Just like a cube becomes a square and a sphere becomes a circle, normals change from being vectors in 3D to being vectors in 2D.
Also, possibly contributing to the confusion is that vectors don't have a a position. A vector is just a direction, and a vector can be placed anywhere.
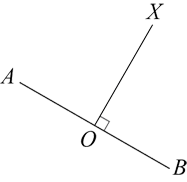
In 3D the normal is perpendicular to a 3D surface. A 3D surface is a plane. So if you have a plane like a flat desk, then you stand a pen on end so it points in the air at a right angle to the surface, that pen is pointing the direction of a the plane or surface normal.
In 2D the normal is perpendicular to a 2D surface. A 2D surface is a line segment or a curve. So if you have a line segment, then you draw a right angle to the line segment, that right angle is the direction of the surface normal.
First of the author said something like this
If we were to retrieve two vectors a and b that are parallel to the surface of the triangle we can retrieve the normal vector by doing a cross product on those vectors
But then what is a surface? Googling it, I think it is just the whole area of a triangle. But then he said "parallel" to the surface. that means this surface has a direction? If I understand parallel vectors. it is a vector that have the same direction. So if we are talking about 2D triangle, at what direction does the surface of the triangle is pointing to? Is this a correct visualization

A normal vector is a vector that is perpendicular to an object at a place. A vector only has a direction, not a location.
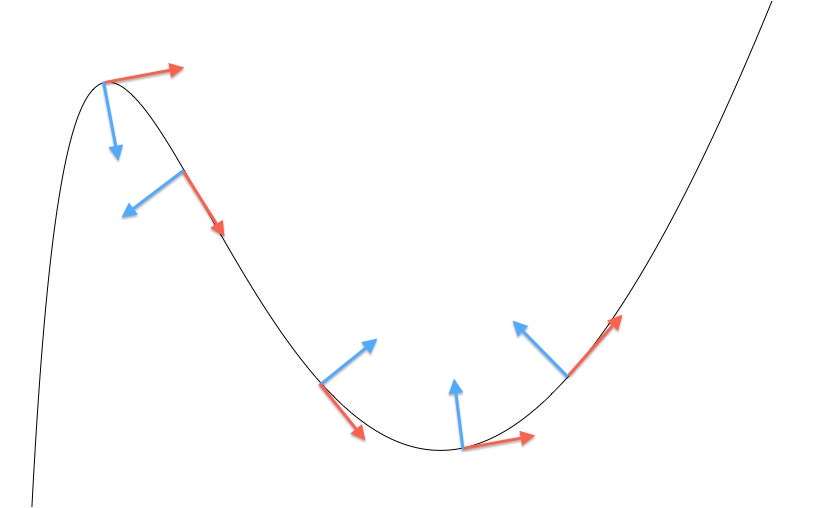
In 2D, a normal vector is perpendicular to a single line or curve. So if you imagine a curve, you've got a tangent line that is parallel to the curve at that point, and a normal line that is perpendicular at that point on the curve. The normal and tangent lines form a "T" shape if you put them along that point.
At the top and bottom of a sine curve, the normal vector would point straight up or straight down.
At any point in a circle, the normal vector would extend out from the center of the circle through that point, like rays from the sun.
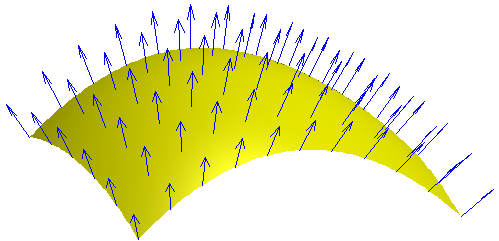
In 3D, the normal vector to a surface is a vector that points directly away from that surface. So if you have a flat desk in front of you, the surface normal points up.
It does not matter if the shape is a triangle or rectangle or hexagon, the surface normal is perpendicular to the surface, pointing up from the surface.
If you have a ball, the surface normal at any point would be like a spiky outward direction.
When they wrote that the vectors were parallel to the plane, it just means they would be flat. It is the direction of the 'flat' at that point relative to the surface or plane. Like an arrow pointing along the edge of a desk, and another different arrow pointing along another edge of the desk. The top of the desk is essentially a plane at that point, and those vectors (that have a direction but do not have a position) would point directly along it.
Second is about plane
The author said something like this
Subtracting two vectors from each other results in a vector that is the difference of the two vectors and since all 3 points lie on the triangle plane, subtracting any of its vectors from each other results in a vector parallel to the plane.
If I am right plane is is about flat shapes. I also going to ask this. if it is flat shape, where is it pointing to?
Is the plane and surface the same here?
thanks
What he describes there is finding two vectors (direction without a position) that is the same direction as two legs of the triangle.
If you are working in 2D then you need to reduce the dimensionality by one. Instead of computing the normal of a 3D object with two vectors, you would need to compute the normal of a 2D curve or line segment.
The normal of a line is similar to a tangent of a line. The normal is perpendicular at that point, the tangent is parallel at that point. The normal points exactly 'away' at that point of the curve, the tangent points exactly 'flat' at that point in the curve.
If you are working with those two vectors you will get a 3D normal. The normal of two legs of a triangle is a direction that points out from the surface of the triangle; drawn on a paper the normal points up out of the paper in 3D. If you want to work in 2D you would find the normal to a single line segment or curve.
This means there is an infinite number of vectors that are parallel to a plane, so all three of the edges of a triangle are parallel to the plane of the triangle.
Still confuse about this. so that means this plane is also the surface? That means in 2D, this plane is facing up or facing to any direction? But let say if the plane is pointing up, does that mean the vertices as well?
No, because you are working in 2D rather than 3D.
Again, vectors are a direction without a position so there are are infinitely many of them. Anywhere in the mathematical universe the vector will remain constant if it has the same direction.
In this case, the vectors point along the direction of the triangle's three legs. If you have a triangle with three points ABC, you can make one vector that points from A to B, one points from B to C, and a third that points from A to C. If you go the other direction, you can have vectors that go B to A, C to B, and C to A.
Since by definition a triangle lies on a single 3D plane, that also means by definition you can use two vectors to define a 3D plane's orientation. It won't find the plane's position because vectors can be anywhere, but it will tell you how the plane is oriented. The normal is perpendicular to that plane.
In 2D you would have a single line or a single line segment rather than a triangle. The normal to that line segment is a perpendicular line, meaning a line that is at a right angle to the line segment.