Hi, I'll try to describe the problem im facing as accurate as I can.

I have two vectors, say A and B and a target direction vector T. I want E = A+B to have the same direction as T. A is the vector (R1,0) rotated by an angle alpha and B is the vector (R2, 0) rotated by 5/3alpha.

So we have this:

A = R1 * (cos(alpha), sin(alpha))
B = R2 * (cos(2/3alpha), sin(2/3alpha))
E = A + B
T = (Tx, Ty)

R1 and R2 are known. T is known as well.

I was thinking of something like:

|E| * normalized(T) = E

I can't seem to solve the equation though, I'm not sure if my trigonometry knowledge is not good enough or if its simply not possible...

Can anyone help me out please?

Thanks!

next time grab ruler, pencil or pen and white paper.then draw the problem or at least draw it in paint, anyway your idea of putting the E to T seems kinda silly but here it is:

or maybe you want to project a vector onto another then this:

//Project A onto B
template <class type> t3dpoint<type>  __fastcall VectorProjectionBDIR(t3dpoint<type> A, t3dpoint<type> B,bool NormalizedB)
{
t3dpoint<type> i = B;

if ( NormalizedB == false ) i = Normalize( i );
type dotp = Dot(A,i);
return i * dotp;

}

Okay seems like I didn't explain the problem properly. Sorry for my poor paint skills...

So I know the length of A and B and I know that the second angle is 2/3s of the first angle (relative to the first). I want to choose alpha, so that E points in the direction of T.

Thanks in advance.

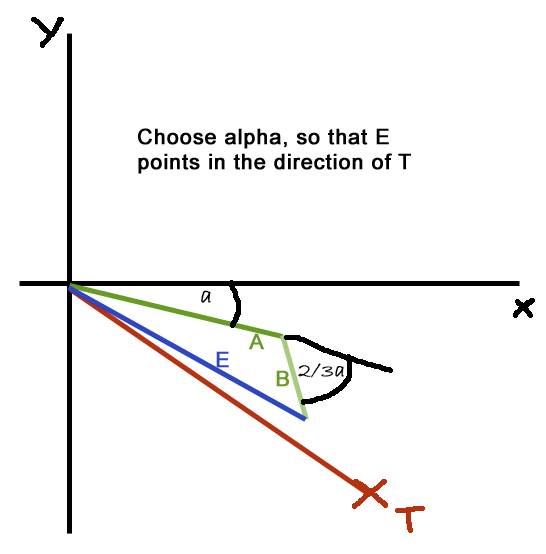
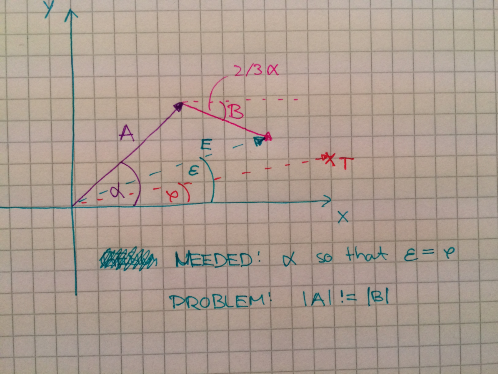
everything is clear now, however your (2/3) * alpha is bigger than alpha and i am not sure why you draw a pic with angles elow x origin since they should be pointed up liek on this picture:

here is my apporach, find angle of T vector, your assumptions (A = R1 * (cos(alpha), sin(alpha))) show that if t points directly right from coord origin then alpha is 0

when alpha is 90 its pointing straight up when 180 then left and when 270 then down. thats how i like it

note i use degrees not radians (for me its more intuitive)

anyway my notebook burned and i am using old one i have no option to compile and test + i had some of my math functions with bugs (not sure if those i show you were bugged, my recent math unit is on other notebook )

const long double pild      = 3.1415926535897932384626433832795;

template <class type> type VALIDATE_TO_360(type angle2)
{
type angle = angle2;

int kat=(int)angle2;

kat=kat/360;

if (angle < 0 )
   angle = angle + (type)(kat+1)*360.0;


if (angle >= 360)
   angle = angle - (type)kat*360.0;

return angle;
}

long double n2dGetPolarCoordAngleAD(double x,double y)
{
if ( (x == 0) && (y > 0) )  { 	return 3.1415926535897932384626433832795/2.0;                   }

if ( (x == 0) && (y < 0) )  { 	return 3.0*3.1415926535897932384626433832795/2.0;                 }

if (x == 0) return 0.0; //actually we cant find the angle
long double k; k = (long double)y / (long double)x;
if ( (x > 0) && (y >= 0) ) { 	return atanl(k);        }

if ( (x > 0) && (y < 0) )  { 	return atanl(k)+2.0*3.1415926535897932384626433832795;  	  }

if  (x < 0)                {	return atanl(k)+3.1415926535897932384626433832795;   	  }




//last versions were without .0 just simple 2 division
return 0.0; //actually we cant find the angle
}

long double GetAngle(vec2 vector)
{
vec2 origin = vec2(0.0, 0.0);
 long double angle;
 angle = n2dGetPolarCoordAngleAD(
 (long double)vector.x-origin.x,
 (long double)vector.y-origin.y) / (pild*2.0);

	   return VALIDATE_TO_360(360.0*angle); //not sure if there should be * 360.0 ut it seems that it should. since i divide with getpolarcoord by two pi
}


now actual function
we define the angles of the A and B so B additionally 2/3 of alpha
1 and 2/3 => 3/3 + 2/3 = 5 / 3

float return_my_angle(vec2 vector)
{
  float angle = float(GetAngle(vector)); //angle between 0-360
//  5/3 * alpha = angle;

return (angle * 3.0) / 5.0;
}

but it should work

so you now have found your alpha

EDIT:

there could be a problem with floating point precision for function

n2dGetPolarCoordAngleAD

with if x == 0 or if y == 0 that needs to be tweaked to use some sort of epsilon like 0.0001 or even smaller so it will assume small numbers as 0.0

Okay thank you first of all, that already helped a little bit, but I'm afraid I dont think this will work. Heres the problem drawn again, this time without mistakes hopefully (sorry about that, it was kinda late for me already).

So the problem is that |A| != |B| and thus your equation of alpha = 3/5*angle won't hold!? Is there any way to extend that relation with the length information of A and B? I couldn't find anything that would help me there..if I had just payed more attention to trigonometry :S

EDIT:

So we know the slope of the target vector, lets call it m.

We can express E as a combination of A and B. This leaves us with

E.x = |A| * cos(alpha) + |B| * cos(2/3alpha)
E.y = |A| * sin(alpha) + |B| * sin(2/3alpha)
m = E.y / E.x

However, I'm not able to solve this..

Okay, someone over at math.stackexchange.com had an answer for me. Looks like it has to be computed numerically.

Thank you for your help anyway ;)

that image was really misleading (talking about that 2/3 alpha)

Yeah, sorry I realised that. Seems like the problem wasnt fully clear to me, yet..