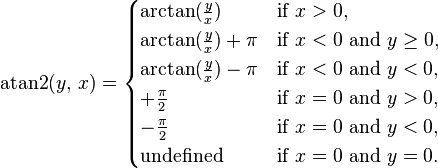Hey guys, can you help me with this?

The problem is about projectile motion. Given an origin point (ox,oy), a target point (tx,ty) and a initial velocity v, I want to find the angle at which the projectile should be launhed from the origin in order to touch the target. This is the formula I found at wikipedia:

Angle required to hit coordinate (x,y) from origin (0,0)

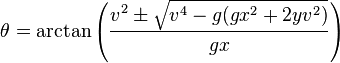
double getAngleToHit(double ox, double oy, double tx, double ty, double v){
    double x = tx - ox;
    double y = -(ty - oy);
    double g = 10;
    return atan2(v*v - sqrt(pow(v,4) - g*(g*x*x + 2*y*v*v)),g*x);
}

double getAngleToHit(double ox, double oy, double tx, double ty, double v){
    double x = (tx - ox)/2;
    double y = -(ty - oy)/2;
    double g = 10;
    return atan2(v*v - sqrt(pow(v,4) - g*(g*x*x + 2*y*v*v)),g*x);
}

The angle returned is not quite right. I watched this code run various times with different parameters and I noticed a pattern... if y is equals 0, that meaning origin and target are on the same height, the result is something like this:

You have not made arcus tangent inverse goniometric function used in wiki formula that equal with atan2 function, see

https://en.wikipedia.org/wiki/Atan2#Definition_and_computation

I don't understand what you mean by that. Can you explain me?

According to C++ standard library documentation, atan2(y,x) is equals to atan(y/x).

As you can see, the relation between atan and atan2 depends on definition values. Since subtracting x and y positions can yield any of those cases, you cannot use "atan2(y,x) is equals to atan(y/x)." assumption that immediate.

May I ask why don't you use atan instead of atan2?

According to C++ standard library documentation, , atan2(y,x) is equals to atan(y/x).

Could you support this statement by some source? It can be true - but I wouldn't think so.

a good summary of the maths can be found here - http://hyperphysics.phy-astr.gsu.edu/Hbase/traj.html#tra12

the above methods seem overly involved to me. not to discount them, they may be more efficient or more accurate - i use a simple approach, which is of course suited for my simple implementation - projectiles have a frame rate "direction" vector and a per-frame "gravity incurrence". i solve this as follows:

1) determine distance to target in frames

2) determine the "gravity incurrence" for this many frames

3) aim that far above the target


step 2 may take a pow operation depending on how gravity is implemented, but generally this method requires a few simple operations.

(and of course should be improved, eg. aiming at where the target will be when the projectile gets there.. implementation can become more involved if you add "is target visible in starting position, is target visible in ending position" various stuff).

the above methods seem overly involved to me. not to discount them, they may be more efficient or more accurate - i use a simple approach, which is of course suited for my simple implementation - projectiles have a frame rate "direction" vector and a per-frame "gravity incurrence". i solve this as follows:

1) determine distance to target in frames

2) determine the "gravity incurrence" for this many frames

3) aim that far above the target

I see what you are doing with your method... While it might be good for what you are doing, I can see that there are two reasons why it may lead to an inaccurate targeting calculation.

The most important reason is that as the firing angle changes the velocity in the X changes, which means that the time (distance to target in frames) will change also. For fast moving projectiles over a shortish distance I don't suppose you will see this as a problem... but over a long range or slow moving projectiles this may be an issue. All projectiles will fall short of the target point by some margin using this method.

The second which is more an game engineering thing than a maths thing, is using number of frame in your calculation is just a substitution for time. If you change it to be time then your method will produce more similar results in a variable-frame rate world when compared to a fixed-frame rate world. As it stands your method may be very incorrect when using a variable-frame rate.

(and of course should be improved, eg. aiming at where the target will be when the projectile gets there.. implementation can become more involved if you add "is target visible in starting position, is target visible in ending position" various stuff).

This relates more to lead targeting which is how far ahead do I need to aim in order to hit them. I have been finding this quite difficult to figure out the maths using a parabolic, though I'm sure an analytical solution exists. It would be awesome to learn the answer if anyone on here knows how to do it. The problem is the same as I described above (as the angle changes so does the flight time) ...In the meantime I'm getting reasonably accurate results using a linear lead target calculation. that is another quadratic calculation using these parameters:

if there is a solution the result is given in time, so the lead is approx:

target_position_vector + target_velocity_vector * time

another reason to make a quadratic solver function. In this case there are also often 2 solutions, you want the smallest.

Thank you all for your help. It turns out I'm dumb, the wiki formula works totally fine like this:

double getAngleToHit(double ox, double oy, double tx, double ty, double v){
    double x = tx - ox;
    double y = -(ty - oy);
    double g = 10;
    return atan2(v*v - sqrt(pow(v,4) - g*(g*x*x + 2*y*v*v)),g*x);
}

The issues I had with the weird trajectory had nothing to do with the angle returned by this function. It turns out I was updating all the entities position twice in my code, which explains why when I divided x and y by 2 the trajectory was correct. So yes, wiki is right.

Moving on, the function requires a check to see if the given speed is enough to hit the target. I'm not a physics expert, so correct me if I'm wrong. In order to guarantee that the speed is enough to touch the target, I need to guarantee that the square root within the formula is not imaginary:

pow(v,4) - g*(g*x*x + 2*y*v*v) >= 0

Solving for v, we have that

v >= sqrt((-2*g*y + sqrt(pow(2*g*y,2) + pow(2*g*x,2))/2))

And the code becomes:

double ProjectileSystem::getAngleToHit(double ox, double oy, double tx, double ty, double& v){
    double x = (tx - ox);
    double y = -(ty - oy);
    double g = gravity;
    double vMin = sqrt((-2*g*y + sqrt(pow(2*g*y,2) + pow(2*g*x,2))/2));
    v = max(vMin, v);
    return atan2(v*v - sqrt(pow(v,4) - g*(g*x*x + 2*y*v*v)),g*x);
}

The way I like to solve this is take the quadratic and pass in the parameters as follows -

double a = ( gravity * relative_distance^2 / velocity^2 ) * 0.5;

double b = -relative_distance;

double c = a + relative_height;

...then I use various solvers depending on the function. In this case something like...

bool solveQuadraticMinimum(double a, double b, double c, double& theta); //getting shortest solution

bool solveQuadraticMaximum(double a, double b, double c, double& theta); //getting highest arc solution

bool solveQuadratic(double a, double b, double c, double& theta1, double& theta2); //getting both...

How did you end up with this quadratic equation for theta? How doesn't it involve any trigonometric function?

1) determine distance to target in frames

2) determine the "gravity incurrence" for this many frames

3) aim that far above the target

I see what you did there but I'm afraid it wouldn't work for my context as pointed by Brum87.

The atan is correct for getting the angle...

You may be getting problems when you solve the quadratic... and in practice the quadratic solution tells you a lot about the solution here.

No quadratic solvings luckily.

It is true that quadratic deviation explains immediate universal attracting force, by Newton law as , dV=m*a; a=F/m F=G* (m1*m2) / r² between two objects, yet the formula of angle retrieving, from provided constant g acceleration, can yield a meeting angle upon this system. It is a big unknown of course if there is a third mass object involved influencingly close. This is only to be a simulated system, not computable, and even precision and timestep greatly influence the pathetic simulation. Newton law is , right now, the only determenistic universal law, yet Newton denied it as "too special" desciption theory, since it would predict a too draconic phenomena for universe , that was believed to not obviosly exist ( unlimited speed attractions)

https://en.wikipedia.org/wiki/Orbit