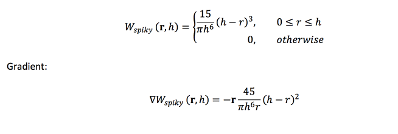Hi am currently breaking down a paper called "Position Based Fluid" and have trouble understanding some symbols.

First off, i dont have any math professional backgrounds at all - i barely understand the basics to break down some formulas but if these gets too complex and i dont have any chance to convert this code.

There is a kernel function for calculation a approximation value based on the difference between two particles - called smoothing function which does some magic math stuff behind, like transforming the distance between two particles into the range of the kernel h with some smoothing...

There are two variants of this formula, one normal and one for gradient:

What are the differerence between those?

I know that means "Change in" and i also found out that the flipped symbol means gradient but i have no clue what this are.

Please help me to break this down.

Thanks and regards,

Final

The gradient is the vector whose coordinates are the derivatives of the function with respect to each variable. But a quick Google search probably already told you that...

It's the Del operator: http://en.wikipedia.org/wiki/Del

Like Alvaro, said, each cooridinate of a gradient vector are the derivatives with respect to it.

For future reference, there's this really nice page that helps me out a lot: http://en.wikipedia.org/wiki/List_of_mathematical_symbols

A more geometrical definition for gradient of a scalar function W is that it is a vector valued function, where the vectors point to the direction where W increasest most rapidly. The length of the vectors indicate how rapidly.

The components of grad(W) are only the coordinate derivatives of W in Cartesian system. Not the case in e.g. spherical coordinates. In most fluid treatments for games, Cartesian coordinates are used, so I don't want to confuse you with this, but it's good to be aware that some definitions are bound to specific coordinate frames while the gradient can be defined in coordinate-free manner.

It may also be useful to know that the "Delta" symbol may refer to the Laplacian, which is a second-order derivative of either scalar or vector function. This may also arise in fluid dynamics.

A more geometrical definition for gradient of a scalar function W is that it is a vector valued function, where the vectors point to the direction where W increasest most rapidly. The length of the vectors indicate how rapidly.

The components of grad(W) are only the coordinate derivatives of W in Cartesian system. Not the case in e.g. spherical coordinates. In most fluid treatments for games, Cartesian coordinates are used, so I don't want to confuse you with this, but it's good to be aware that some definitions are bound to specific coordinate frames while the gradient can be defined in coordinate-free manner.

Yes, you can define the gradient intrinsically (i.e., without referring to coordinates), but be aware that this definition depends on a metric. The exterior derivative of a function at a point is a covector, and a metric allows you to map that to a vector.

I was going to mention this in my first post, but it's unclear to me how this would help the OP.

Ah i see, so basically its just a vector as returning value?

Yes, it's a vector.

One important way to think about the gradient is that if you have a physical system with some associated potential energy function, the corresponding force is minus its gradient. See http://en.wikipedia.org/wiki/Potential_energy#Forces.2C_potential_and_potential_energy .

I have trouble converting the following formula into its gradient form:



My code for this:

private float Wspiky (Vec2f r, float kH) {
	float rlen = r.length();
	if (rlen > kH || rlen == 0) {
		return 0;
	}
	final float tmp = kH - rlen;
	final float term = 15.0f / ((float)Math.PI * (float)Math.pow(kH, 6));
	return term * tmp * tmp * tmp;
}

I found a image for a gradient version, but my implementation of this produces wrong results:

private Vec2f gradWspiky (Vec2f r, float kH) {
	float rlen = r.length();
	if (rlen > kH || rlen == 0) {
		return new Vec2f (0f, 0f);
	}
	final float tmp = kH - rlen;
	final float term = 45.0f / ((float)Math.PI * (float)Math.pow(kH, 6) * rlen);
	return r.mult(-term * tmp * tmp);
}

I dont see any mistake.... please help me.

I dont see any mistake.... please help me.

Assuming that the math routines do what I think they do, this seems fine. How do you know it is not working? Have you plotted the result to see if it looks like you might expect from the geometric interpretation of the gradient?

A word of warning: I once tried out particle hydrodynamics for some fluid simulations. I never got good results, because there are alot of parameters to play with and it requires a lot of iteration to get things work reasonably. Worst of all, usually the behaviour depends sensitively on the number of included particles and the chosen timestep. Change the timestep and all other parameters may need to be revisited.

I dont see any mistake.... please help me.

Assuming that the math routines do what I think they do, this seems fine. How do you know it is not working? Have you plotted the result to see if it looks like you might expect from the geometric interpretation of the gradient?

A word of warning: I once tried out particle hydrodynamics for some fluid simulations. I never got good results, because there are alot of parameters to play with and it requires a lot of iteration to get things work reasonably. Worst of all, usually the behaviour depends sensitively on the number of included particles and the chosen timestep. Change the timestep and all other parameters may need to be revisited.

Yes i know that tuning SPH parameters are really hard - i made some fluid simulations in the past (Fluid Sandbox) based on physX SDK, but even with an existing physics engine it taked me weeks to figure out some paramter configurations which works - almost. There was over 20 parameters for PxParticleFluid to set... pain .... but fortunatly the paper i am targeting right now, just have a few parameters and support small time steps without doing any sub steps.