This is not interference involved also not precision errors or something, this is just a stable way of colorisation of the sphere also i think it has an infinite indepth complexity here (if you wil rize up the palette frequenzy to infinite, as i said, ), here is some 'zoomed' example yet
The circles form one pattern, and the pixels forming the discrete sampling grid is the second pattern. The interference is implicit from the intersection between the two patterns when you sample the continuous circle pattern at the discrete pixel grid.
 some.jpg
some.jpg
Overlay that image and the one from your first post and you'll see that the interference patterns, or fractals if you want, are not the same; neither at the equivalent scaled location or at the equivalent scaled size. Your patterns are thus resolution dependent. That's precisely how interference works.
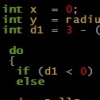
I changed the palette frequenzy up 5times (by putting the ball more far now its centre is 5 km far and has a radius of 3.5 km) in the second picture as i said more details is wisible when rising up the palette frequenzy - what is interfering with what? (I do not see a need of talking
about this interferentions here, i do not see them, it would be better to talk about math structure of this pattern, but i m not to much educated in hyperbolic geometry or such things)
ps probably i could rise up the visual effect by defining nicer palette
(but not sure if got a time to do this today)