Hi,

I have always wondered on this, may be i am missing something very simple, in the perspective shadow map calculation from the paper: http://www.cs.berkeley.edu/~ravir/6160-fall04/papers/p557-stamminger.pdf

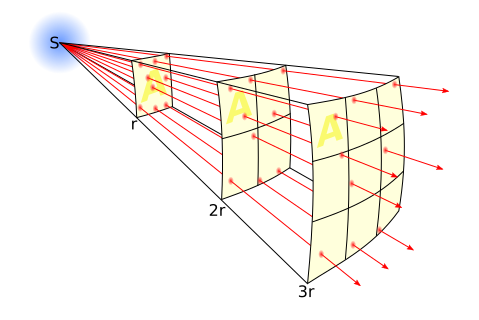
In section 1.1, it mentions that when a ray bundle from shadow map hits the surface at a distance r_s with an angle substended at alpha, and the shadow map pixel width is d_s, the lenght of the surface hit is equal to approximately: d_sr_s/(cos(alpha).

How do we arrive at this derivition?

Any help is much appreciated.

Thanks,

obhi

The ds * rs part is the inverse square law. Here you are only considering the width and not the whole area, so it increases linearly with distance as you would expect (if you stare at an object through a camera at a distance D and see it records a length of X pixels, then walk back to a distance 2D, its length will have decreased to X/2 pixels).

The cosine division part is basically the cosine law in action:

So as the angle approaches 90 (grazing) the perceived length gets smaller and smaller. So if you start with a ray bundle that hits a surface with an perceived width of ds, the true length is going to get larger as the angle tends to grazing (here think of ds as the width of the blue beam). Of course if you are looking at it at normal incidence, then its true length is the same as its perceived length, and cos(alpha) = 1 as expected.

So at 2D the lenght becomes X/2, which means a the surface pixel count should be (for rs units) rs*ds. And the blue line: d*cos(theta) = percieved length = rs*ds (from inverse sq).. Thanks a lot :)

So at 2D the lenght becomes X/2, which means a the surface pixel count should be (for rs units) rs*ds. And the blue line: d*cos(theta) = percieved length = rs*ds (from inverse sq).. Thanks a lot

Yes, that's right (sorry for the typo, it's late - fixed)

No problem, you provided a very helpful pictorial explanation :)