see the following image…

The voxels are contained in an octree, this is an 8-leaf tree, each leaf being an eighth of the cube containing each node.

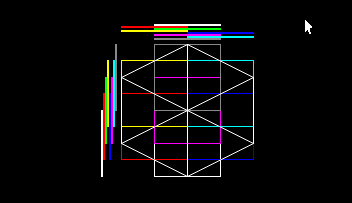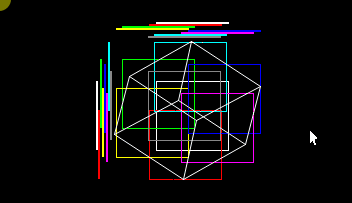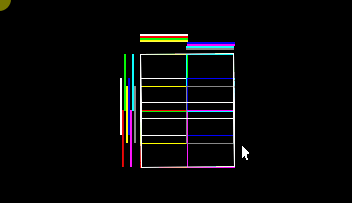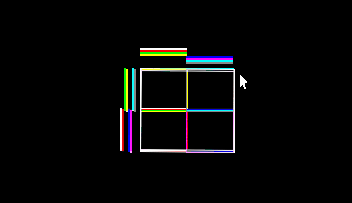
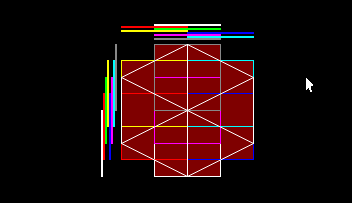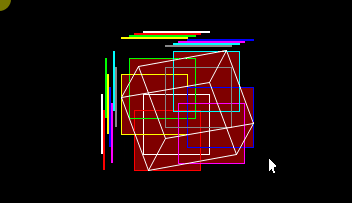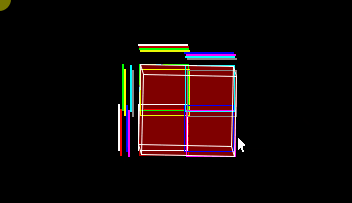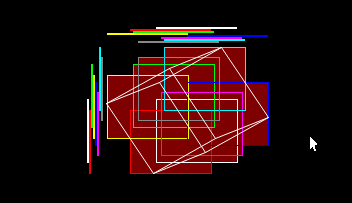
In the image you can see the cube of the root of the octree, the algorithm will draw the voxels inside this isometric cube.

The colored boxes are what each sub cube occupies in 2d, and the lines above and on the left correspond to the occupation in that dimension.

One of the properties of the octree is that given the point of view it is possible to travel the entire tree so that the voxels are drawn correctly

If I go through the box containing the cube (rasterization) and I only paint when there is a possible children, that is, it must have the indication in X and Y that that sheet exists at the same time.

We get a painted of the children of the octree, you can see that the silhouette is correct.

The existence of the children can be checked by having two byte arrays, the X mask and the Y mask, the colored lines on the sides

The children of a point in X,Y and will be: maskX [x] AND maskY [y], only two access to memory and one boolean operator.

The next thing we notice is that in an isometric perspective, this diagram is repeated for each child exactly half the size in 2d.

If it is repeated for each child, in order of view and entering only the nodes that exist in the octree to the level that the size is a pixel or the octree is finished, the correct image of the octree should be obtained.

You can see here in red when the first level has no children, when you have children but the node in the octree no, is in blue, then it paints in lighter blue when you did not find a voxel in the last level and if not, the color of the voxel found

It should be clarified, the order of travel of the octree is not correct, the use of the isometric perspective changes the way of calculating this and I am not finished