Collision detection is an important part of most 3D games. Shooting enemies, avoiding (or failing to avoid) obstacles, even simply staying on the ground usually requires some form of collision-detection. It's a vast subject and there are many excellent articles written about it. However, most of them concern the more sophisticated algorithms, such as BSP and the simple bounding-sphere check receives no more than a passing mention. It is a quite simple procedure but it still could be very useful and there are a couple of subtle points involved. So I thought perhaps I should write something about it.
[size="5"]Straightforward version
The simplest possible way to do bounding-sphere test is to measure the (squared) distance between the two objects in question and to compare the result with the (squared again) sum of their radii. The reason we use the squared distances is to avoid the costly square-root calculation. The code will look something like this:
BOOL bSphereTest(CObject3D* obj1, CObject3D* obj2 )
{
D3DVECTOR relPos = obj1->prPosition - obj2->prPosition;
float dist = relPos.x * relPos.x + relPos.y * relPos.y + relPos.z * relPos.z;
float minDist = obj1->fRadius + obj2->fRadius;
return dist <= minDist * minDist;
}Note: This and the following code snippets use the D3DVECTOR type from Microsoft's Direct3D, if you are using some other 3D library, change the code accordingly.
This procedure is easy indeed and some cases may be even adequate but what if your objects are moving at a considerable speed? Then it could happen that at the beginning of a frame the bounding spheres do not intersect yet by the end of the frame they have passed through each other. If the distance your objects travel in one frame is greater than the size of the object this scenario is quite likely. Clearly we need something more advanced to handle this case.
[size="5"]Improved version
What we need is to somehow incorporate the object velocities into the calculation. That is quite simple if you do just a little bit of vector math (you can skip this section if you have a math phobia).
Let
and 
be the positions of the objects at the time 
.We'll take 
at the beginning of the frame and 
at the end of the frame. Also let 
and 
be the velocities of the objects. Then
Equation 1
and their relative position will be
The distance between the objects will be just the magnitude of the relative-position vector or, which is the same thing, the square of the distance will be equal to the square of the vector:
Note: I use * to denote the dot product between two vectors.
Now all we need is to find if
ever gets less than the minimal allowed distance 
(i.e the sum of the radii of the bodies) during the next frame, that is between
and 
.The way to do it is to check if the distance already less than the minimal (we might have somehow missed the collision on the previous frame, because of physics and AI corrections or whatever) and if not then we need to solve the equation
. This will be the moment when the objects are exactly at the distance . Generally there will be two such cases- corresponding to the moments when the bounding spheres touch for the first time and when they touch for the last time after passing through each other. You will probably be more interested in the former, that is the least of the two values. If we write everything out we get:
I have omitted [0] to make the formula more readable.
This is a simple quadratic equation and we solve it in the usual way, by finding the determinant:
Equation 2
If D<0 then the equation does not have a solution, that is the spheres do not collide at all. If D>0 then the spheres collide (if D=0 then the spheres merely touch each other, you can handle this case either way, depending on the specifics of the situation). The roots of the equation are:
Equation 3
Then we can take
, test if it is between 0 and 1 and if it is then we have the collision. It's straighforward enough but we can take a few shortcuts for the sake of optimisation. First of all, and this is just an arithmetic manipulation, we can cancel the 2's:
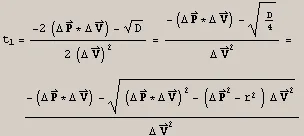
Second, and more important we can test if the roots are between 0 and 1 even before calculating
, in fact even before calculating D. To see how, note that
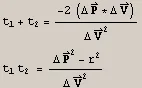
Equation 4
This is a case of what is called Viete's theorem. Let's look closer at this, specifically let's look at the signs of these values. If
then we can say for sure that 
and 
. In that case the collision is already in progress - the spheres are intersecting each other right at the beginning. If 
but 
then both 
and 
and that is another easy case - the spheres are flying away from each other and no collision is going to happen.To make these cases even easier note that the denominators in both cases are greater than 0 - just like the square of any real number. (if they are equal to 0 then the relative speed of the spheres is 0, not moving at all. Then everything is just like in the previous section). Therefore the signs of these expressions are the same as the signs of their numerators. The numerator of the second expression is just the square of the distance between the spheres at t=0 minus the
- the square of the minimal allowed distance. That is exactly what we have calculated in the code snippet 1. So we are going to reuse that code in our new and improved version! Calculating 
will be our next step, we'll need that value later anyway.Ok, so we can find the cases where solution is <0 that is when the collision has already happened. Now we need also to weed out the cases when the solution is >1. That is the collision might happen but not within the next frame, so we are not interested. (if you are interested in these situations as well just skip this check). To find out we just write the condition out:
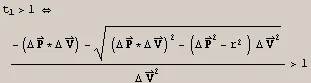
Or, after some algebraic manipulations, we arrive at these 2 conditions
If these two inequalities hold true then
and we know there is no collision withing the next frame.Now, If we passed all the tests then we have no choice but to calculate D and see if it is >0. If you wish to know the exact time (or position) of the collision then you can go on and calculate its square root, find
and so forth. In my code I'll skip those steps for simplicity.BOOL bSphereTest(CObject3D* obj1, CObject3D* obj2 )
{
// Relative velocity
D3DVECTOR dv = obj2->prVelocity - obj1->prVelocity;
// Relative position
D3DVECTOR dp = obj2->prPosition - obj1->prPosition;
//Minimal distance squared
float r = obj1->fRadius + obj2->fRadius;
//dP^2-r^2
float pp = dp.x * dp.x + dp.y * dp.y + dp.z * dp.z - r*r;
//(1)Check if the spheres are already intersecting
if ( pp < 0 ) return true;
//dP*dV
float pv = dp.x * dv.x + dp.y * dv.y + dp.z * dv.z;
//(2)Check if the spheres are moving away from each other
if ( pv >= 0 ) return false;
//dV^2
float vv = dv.x * dv.x + dv.y * dv.y + dv.z * dv.z;
//(3)Check if the spheres can intersect within 1 frame
if ( (pv + vv) <= 0 && (vv + 2 * pv + pp) >= 0 ) return false;
//Discriminant/4
float D = pv * pv - pp * vv;
return ( D > 0 );
}[size="5"]One more improvement
The code in snippet 2 works quite well in many circumstances but there's a little problem with it. It is not a mathematical problem but a computer-related one. Think about the very last calculation
float D = pv * pv - pp * vv;BOOL bSphereTest(CObject3D* obj1, CObject3D* obj2)
{
//Initialize the return value
*t = 0.0f;
// Relative velocity
D3DVECTOR dv = obj2->prVelocity - obj1->prVelocity;
// Relative position
D3DVECTOR dp = obj2->prPosition - obj1->prPosition;
//Minimal distance squared
float r = obj1->fRadius + obj2->fRadius;
//dP^2-r^2
float pp = dp.x * dp.x + dp.y * dp.y + dp.z * dp.z - r*r;
//(1)Check if the spheres are already intersecting
if ( pp < 0 ) return true;
//dP*dV
float pv = dp.x * dv.x + dp.y * dv.y + dp.z * dv.z;
//(2)Check if the spheres are moving away from each other
if ( pv >= 0 ) return false;
//dV^2
float vv = dv.x * dv.x + dv.y * dv.y + dv.z * dv.z;
//(3)Check if the spheres can intersect within 1 frame
if ( (pv + vv) <= 0 && (vv + 2 * pv + pp) >= 0 ) return false;
//tmin = -dP*dV/dV*2
//the time when the distance between the spheres is minimal
float tmin = -pv/vv;
//Discriminant/(4*dV^2) = -(dp^2-r^2+dP*dV*tmin)
return ( pp + pv * tmin > 0 );
}[size="5"]Conclusion
So here it is, the bounding-sphere collision detection algorithm. It might be useful as is (say, for a pool game) or can be a quick-and-dirty test before doing a more sophisticated check - polygon-level, for instance. You may also want to try to improve the accuracy of the collision detection by using a hierarchy of bounding spheres, breaking your object into several parts and enclosing each of them in a bounding sphere of its own.
//Discriminant/(4*dV^2) = -(dp^2-r^2+dP*dV*tmin)
return ( pp + pv * tmin [color=#ff0000][font=arial,helvetica,sans-serif][i][b]<[/b][/i][/font][/color] 0 );