The well-known Weiler-Atherton Algorithm of the polygons clipping usualy is demonstrated in 2D performance. Nevertheless this idea also works in 3D. The demo programs concerned Weiler2D.exe and Weiler3D.exe are in the Weiler3D directory to be unpacked from the attached article resource archive.

1. Weiler-Atherton in 2D

The Weiler-Atherton Algorithm of the two 2D polygons may be performmed as 3 steps:

1. To create the set of segments consisted of the vertexes of the 1st polygon contained inside the 2nd polygon the points of the ribs intersection included.
2. To create the set of segments consisted of the vertexes of the 2nd polygon contained inside the 1st polygon the points of the ribs intersection included.
3. To merge the sets of segments above with the intersection points.

The following illustrations have been created with the Demo Program Wailer2D.exe: In fig 1.1 two randomly created polygons Red and Blue to be clipped.

In fig 1.2 the set of Magenta segments of the the vertexes of the Red polygon are contained inside the Blue polygon and the set of Aqua segments of the the vertexes of the Blue polygon are contained inside the Red polygon.

In fig 1.3 The sets of Magenta and Aqua segments are moved aside for the demonstration purposes.

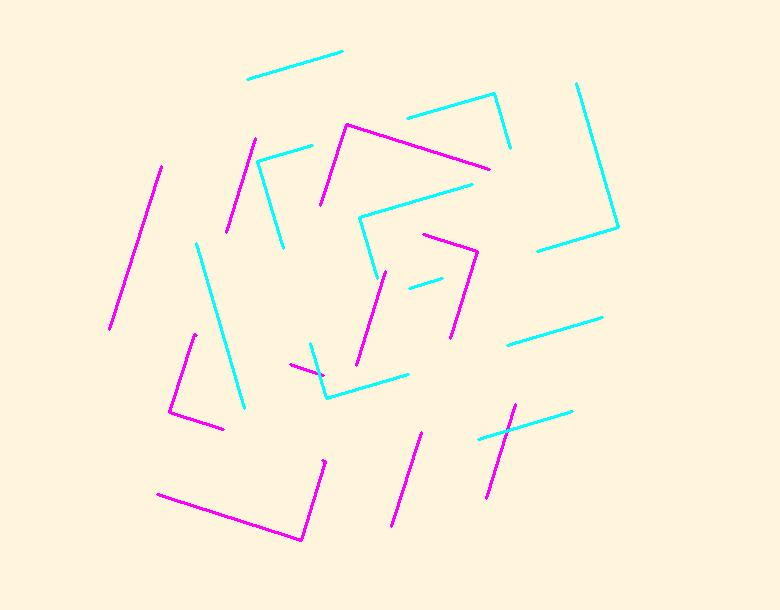
In fig 1.4 The sets of Magenta and Aqua segments are moved together to create clipping polygons.

In fig 1.5 the the Yellow clipped polygons are shown together with the original Red and Blue polygons.

You may create your own performance of the 2D Weiler-Atherton Algorithm with the program Wailer2D.exe. To watch step by step performance use the Right Arrow button while the Play timer is stopped. To start clipping press Enter button. All the commands for Weiler2D.exe available are shown in the Help Dialog (press F1 button to show)

To start the new scenario just press Space Bar. The polygons are randomly created and randomly oriented and randomly rotated.

2.Weiler-Atherton in 3D

The Weiler-Atherton Algorithm of the two polyhedrons clipping may be performmed as 3 steps:

1. To create the set of polygons consisted of the vertexes of the 1st polyhedron contained inside the 2nd polyhedron the points of the polygons inertsection included.
2. To create the set of polygons c consisted of the vertexes of the 2nd polyhedron contained inside the 1st polyhedron the points of the polygons inertsection included.
3. To merge the sets of polygons above with the inersection points.

The next illustrations has been arranged with the Demo Program Wailer3D.exe: In fig 2.1 two randomly created Red and Blue polyhedrons randomly oriented to be clipped.

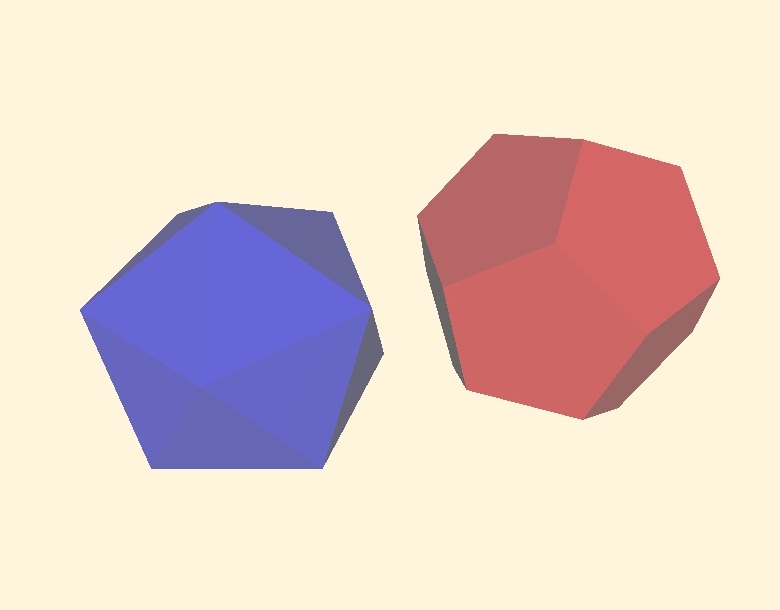
In fig 2.2 the Red and Blue polyhedrons moved into random position to start clipping.

In fig 2.3 the Red and Blue polyhedrons in random position are shown in blending mode as semi-transparent.

In fig 2.4 the sets of the Red polyhedron faces inside the Blue one and the sets of the Blue polyhedron faces inside the Red one the segments of intresection included are moved aside for the demonstration purposes.

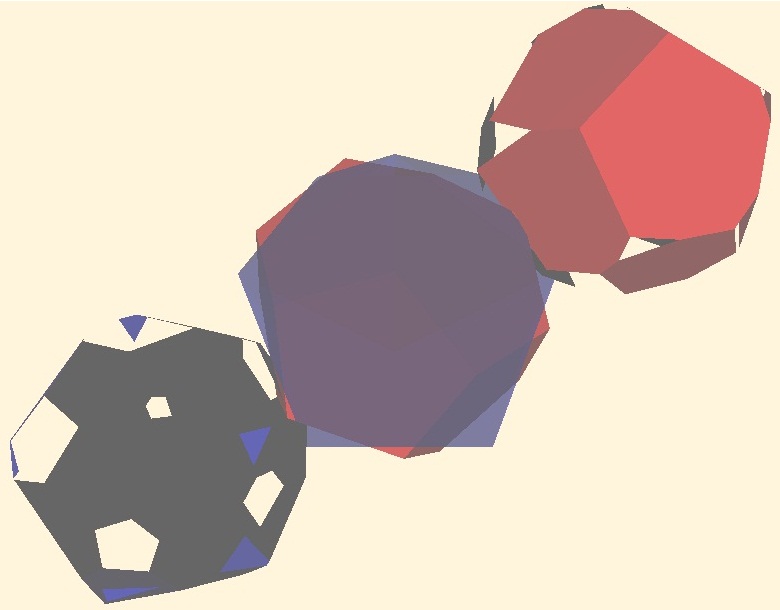
In fig 2.5 the sets of the Red polyhedron faces inside the Blue one and the sets of the Blue polyhedron faces inside the Red one the segments of intresection included are moved together to obtain the clipped polyhedron.

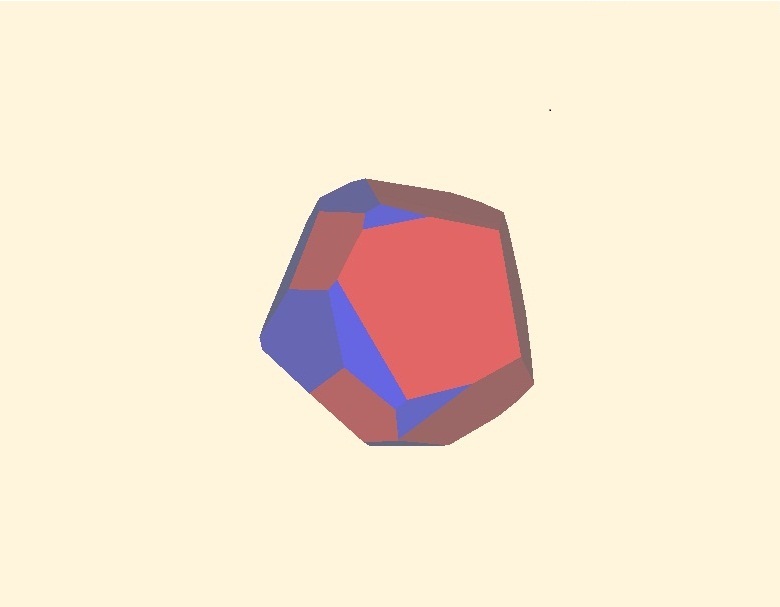
You may select Play menu to watch the clipped polyhedron faces and/or you may use Mouse move with the left mouse button pressed. To watch step by step performance use the Right Arrow button while the Play timer is stopped. All the commands for Weiler3D.exe available are shown in the Help Dialog (press F1 button to show)

To start the new scenario just press Space Bar. The polyhedrons are randomly created and randomly oriented and randomly rotated. The programs above have been developed on the MFC platform. Needless to say that it is not a problem to develop them in Win32 or any other platform. The pseudocode of the procedures used in Weiler3D are provided below:

declare: 
    Plane : space area determined with the normal vector and the distance of axis centre 
    Polygon: list of the vertices layed in one plane 
    Polyhedron: list of the polygons conected 
    
////////////////////////////////////////////////////////////////// 
Procedure main 
begin 
    Polyhedron Red 
    Polyhedron Blue 
    Polyhedron Mixed 
    ClipPolyHedrons( Red, Blue, &Mixed) 
end Proc

////////////////////////////////////////////////////////////////// 
Procedure ClipPolyhedrons( Polyhedron p0, Polyhedron p1, Polyhedron * pRslt) 
begin 
    ClipPolyhedronIn(Polyhedron p0, Polyhedron p1, Polyhedron * pRslt) 
    ClipPolyhedronIn(Polyhedron p1, Polyhedron p0, Polyhedron * pRslt) 
end Proc 

/////////////////////////////////////////////////////////////////// 
Procedure ClipPolyhedronIn( Polyhedron p0, Polyhedron p1, Polyhedron * pRslt) 
//pRslt is a list of polygons of Polyhedron p1 contained inside 
//the Polyhedron p0 intersected polygons including 
begin 
    with Polyhedron p0 for every polygon Polygon 
        pCur = the current polygon; 
        Polygon pNew = the result of the intersection of the Polygon pCur and Polyhedron p1 
        IntersectPolygon(p1, pCur, &pNew) 
        
        if there are any vertices in the Polygon pNew 
            Polygon pNew is appended to the polygon list in Polyhedron * pRslt 
        end if 
    end for 
end Proc 

///////////////////////////////////////////////////////////////////////////// 
Procedure IntersectPolygon(Polyhedron phdr, Polygon plgn, Polygon * pRslt) 
//pRslt is a list of vertises of Polygon plgn contained inside 
//the Polyhedron phdr vertises of the intersection including 
begin 
    if Polygon plgn is completely inside of the Polyhedron phdr 
        make Polygon * pPslt as copy of Polygon plgn; 
        return; 
    end if 
    
    Plane pA //The Plane of the Polygon plgn vertices 
    Polygon pT //The Polygon obtained with the intersection of the Polyhedron phdr by the Plane pA 
    IntersectPlane(phdr, pA, pT); 
    
    if Polygon pT has no vertices 
        return; 
    end if 
    
    ClipPolygons(plgn, pT, pRslt); 
end Proc 

////////////////////////////////////////////////////////////////////////// 
Procedure IntersectPlane(Polyhedron phdr, Plane pA, Polygon * pRslt) 
//pRslt is a list of vertises of the intersection Polyhedron phdr by the Plane pA 
begin 
    with Polyhedron phdr for every polygon Polygon pCur = the current polygon; 
        if all the vertices of the Polygon pCur layed in the Plane pA 
            make Polygon * pPslt as copy of Polygon pCur; 
            return; 
        end if 
        
        let plt - the list of vertices of the intersection of the Polygon pCur with the Plane pA 
        IntersectByFlat(pCur, pA, &plt); 
        
        with the list of vertices plt for all the vertices 
            if current vertice is not in the list of the Polygon * pRslt 
                append current vertice to the list of the Polygon * pRslt 
            end if 
        end for 
    end for 
end Proc 

////////////////////////////////////////////////////////////////////////// 
Procedure IntersectByFlat(Polygon plgn, Plane pA, list of intersection vertices &plt) 
begin 
    with Polygon plgn for all the vertexes let pV = the current vertex; 
        let pVn = the next vertex in the list Polygon plgn 
        double d0 = Distance of pV to Plane pA; 
        double d1 = Distance of pVn to Plane pA; 
        
        if(d0 > 0 && d1 >= 0 || d0 < 0 && d1<=0) 
            continue; 
        end if 
        
        Intersection vertex pU: 
            Vector * pU = new Vector(* pV -(* pVn - * pV)*d0/(d1 - d0)); 
            Append vertex pU to the list of vertices plt 
    end for 
end Proc 

///////////////////////////////////////////////////////////////////////////////////

The pseudocode of the ClipPolygons procedure has been ommited because it is a standard Weiler-Atherton algorithm in 2D. A lot of links concerning this algorithm can be found just by typing "Weiler-Atherton" in a search box (e.g. Weiler-Atherton Algorithm)

Conclusion

The Demo above shows that the Weiler-Atherton Algorithm of clipping is working in 3D as well. The Weiler3D.exe has been created on the basis of NeHe's OpenGL Lessons mentioned in my former article. It seemed worth to use the Weiler-Atherton Algorithm of clipping in 3D simple applications and I believe it will work in 4D and 5D as required.