I've taken the liberty to modify the 'vitals' area simply because I've moved, and no longer wish my address or phone number to be public (marriage has the tendency to do such things
Aside from that, this is the original, unmodified FAQ. There have been no updates and there probably won't be any (I'm using S-Buffers for a project with which I'm contracted under NDA.)
A note from the author:
This may be a bit wordy at times, so I'll try to keep it light with some of my humor -- you may not call it humor, but at least *I* think it's funny.
Where did they come from? s-Buffers were developed for my game engine. Though, since I don't believe that FAQs should have anything to do with commercialization, I won't even mention the name of this product. Let's keep FAQs for their purpose -- FACTS.
The technique described in the next few hundred lines of text bears a close resemblance to some scanline rendering methods of which I believe span-buffering is one of them.
Actually, I had no idea what span-buffering was until I spoke to a gentleman named Chris Babcock who read the original posts about s-buffering. He explained to me what span-buffering was, and as it turns out, the two techniques are similar, but do have some major differences (mainly the Insertion routine and segment manager).
The major difference is that s-Buffers are more so meant for use in game engines. Engines that are meant to produce a high frame rate.
When I posted a note to the rec.games.programmer newsgroup about the fact that I had discovered a technique that would perform z-Buffers in software faster than hardware could, the response was, quite literally, overwhelming. Most of which was plagued with polite suspicion and skepticism. This alone told me that, at least, in the gaming community, this technique was unfamiliar territory. So, I propose to you, the game developer, a new technique, called s-Buffering.
The particular implementation of this technique and it's name are both my own original creation, sparked by my own, sometimes wry thoughts. This FAQ and the techniques contained within are also all my own creation. This isn't to say that there isn't somebody else out there that has once thought about these techniques or variations thereof. I have no control over their thoughts (and wouldn't want to -- Ewwwwww!). I am quite confident, however, that this technique is not popular, not documented, and not in wide use within games.
If you find the information contained within these words, diagrams, and psudo-codes useful to any degree, please contact me. If you use this technique in a product (commercial or otherwise) that you would not have done so if it had not been for this FAQ, please just drop me a line and let me know. It's nice to hear those things. Hearing good things about efforts like this can only spark more.
I would also encourage anybody and everybody to dig in. Play with this new technique. It's not perfect, and the "Insertion" routine can be it's own line of discussion -- inventing many new algorithms for insertion can very possibly improve the performance of this technique in quantum leaps. I would expect that if this technique gains any popularity, you'll see new insertion algorithms popping up in the next Siggraph Proceedings.
I'll be the caretaker of this document. Please make all corrections through me by contribution (internet e-mail preferred).
If you do have other useful information related to this FAQ, !PLEASE! contact me. I may very well want to include it in future versions of this FAQ. Lets keep the InfoBahn alive, let's contribute to it, and share ideas. We've got a hell of a lot of brains out there to draw from.
Striving for speeeeed,
Paul Nettle
Hot Wax Software
"And now for something completely different. A man with six-hundred
thirty-two-thousand four-hundred and forty-two big toes."
[size="3"] Q: "How do I contact Paul?"
My vitals are:
[bquote][This section removed due to a change of address][/bquote] NET: [email="midnight@grafix3d.dyn.ml.org"]midnight@grafix3d.dyn.ml.org[/email]
Please, the name's "Paul", not "Mr. Nettle"
[size="3"] Q: "OK, so what the heck is this all about?!!"
The movie "Weekend at Bernies" quotes this line:
[bquote]"He's got good form!" [/bquote]I think that's one of my favorite quotes because, to me, it has a serious side other than it's humorous description of a corpse being dragged behind a moving boat by a rope, braining itself on buoys along the way.
"Good form" is "Elegance."
Webster defines "Elegant" as:
[bquote]"Marked by concision, incisiveness, and ingenuity; cleverly apt and simple" [/bquote]I couldn't have said it better, Noah. Since elegance is a goal and not a destination, it's something that's to be strived for. You can't reach pure elegance since there is always *something* that's more elegant (the human body, for example).
I hope you find s-Buffers to be "simply brilliant." Not that I'm the brilliant one, mind you, I only discovered the technique. The technique then just started to jump up and down, wave it's arms, blare sirens, and was later found to be screaming out it's advantages at me. I'm just writing them down.
So, back to the question. What's this all about? Elegance, Simplicity and, of course, Speeeeeeeeeeeeeeeeeeeeeeed!
[size="3"] Q: "Why s-Buffers?"
First, consider z-Buffers. If you're not sure EXACTLY how they work, I'll explain briefly:
[bquote]A z-Buffer is a `second copy' of the screen-image. It usually has the same resolution. This z-Buffer is initialized to the largest possible value held by an UNSIGNED INT (for 16-bit INTs, that's 0xFFFF, and for 32-bit INTs that's 0xFFFFFFFF).
During the drawing of polygons, the depth-value for each pixel written has to be kept track of. As you draw each pixel in a polygon, you compare the depth-value of that pixel with the value in the z-Buffer's corresponding pixel location. If the z-Buffer value is larger (farther away from the camera), then the pixel is plotted, and the z-Buffer is updated with the new pixel's depth. If the z-Buffer value is lower (closer to the camera), then the pixel is not drawn since it is hidden behind the existing pixel.[/bquote]This is a very simple approach, and, depending on implementation, can offer pixel-perfect output. However it is very slow and cumbersome.
Your code's inner-most loop (the code that's doing the drawing of the pixels) -- the same code you've hand-assembled for speed is being used to waste clock cycles as if they're as rich a commodity as Madonna CDs. Even if that mean-ol-nasty z-Buffer says the pixel is hidden, you still need to track your deltas. You still have to keep moving through your shades, texture maps, bump maps, colors, etc.
So, you've had to add depth-tracking as well as a slow check to another buffer (possibly outside of your CPU's cache), and a conditional update to that buffer. Whew...what a waste. Such a waste in fact, that I plan to tell you how s-Buffers are not only FAST, but FASTER than z-Buffering in HARDWARE. Keep reading, it's all in here.
Is there a more elegant solution? I believe I have found one. I call it, simply, "s-Buffering."
[size="3"] Q: "What are s-Buffers?"
`S-Buffers' or `segmented-Buffers' are the segmented representation of a z-Buffer. They have three key elements:
- An array of linked-lists (for this example)
- An insertion routine for inserting segments into the s-buffer
- A segment manager
[size="3"] Q: "What is...KEY ELEMENT #1: The s-Buffer itself"
For the sake of simplicity, I'll just use a linked list, later, this can be expanded upon. It's the concept I'm trying to get across here.
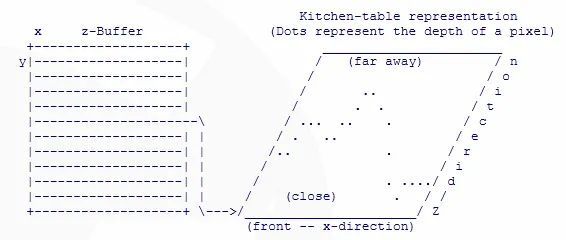
Let's consider our trusty friend, the z-Buffer. Pull out a single scanline from the z-Buffer and set it's representation on the kitchen table (watch out, don't set it in the little puddle of spaghetti sauce).
You now have a single plane. Across the front is the x-direction through a scanline. As you run your finger from the front to the back you're moving it along the depth axis (z-axis). Now go wipe that spaghetti off your finger.
When you look at the entire z-buffer, you're looking at a stack of these planes (that's not true at all, but I want you to think of it that way for now). So, lets just consider the kitchen-table representation.
For each scanline in the z-Buffer, what you have is a list of depth values for each pixel. Even though you may only have a single polygon on the screen, and the depth values in the z-Buffer that the polygon occupies are all the same (it's orientation is perpendicular to the z-axis), you still have to check each pixel, right? Not any more.
From now on, I don't want you to think in terms of pixels. I want you to think in terms of the segments that make up that polygon. In our case, we'll stick with horizontal segments (though orientation isn't important).
When you scan convert a polygon, you break it up into horizontal SEGMENTS:
This is the key to s-Buffers. Now you have a list of segments. Rather that calling any low-level drawing routines to draw these segments, just simply call the s-buffer "insertion" routine.
No, this isn't going to be easy. The "insertion" routine can be a beast all by itself. But, there is a simple 'starter' algorithm that I've included here.
When you're all done scan-converting your polygons and adding your segments to the s-Buffer, what do you have?
You have the ENTIRE screen in a well-formatted, nicely laid out fashion. All the data is in one place, too. The screen is laid out top-to-bottom and each scanline is left-to-right. Can you think of any possible optimizations to take advantage of here? I sure can.
Now it's time to call your 'modified' low-level drawing routine. But first, a glance in the past. In a lot of applications, the low-level drawing routine might look something like this:
void LowLevelDrawer( int x1, int x2, int y, int shade1, int shade1, int Color)
{
[lots of setup code, clipping, etc.]
.
.
.
[draw the scanline]
.
.
.
[any exit code]
.
.
.
[return]
}See all them parameters (I count 6)? That's just for a single piece of a single polygon for a simple gouraud shader. What about a bump-mapper and texture-mapper? Your stack will hate you for that, you're driving it nuts! Push, Pop, Push, Pop, Push, Pop....
Here's a peek at your NEW and IMPROVED s-Buffer drawing routine. It draws the ENTIRE screen:
void LowLevelDrawer( SBUFFER *Sbuf )
{
while( !Done )
{
[do a little setup for this scanline]
.
.
.
[draw all segments for a single scanline (optimized code goes here)]
.
.
.
[next scanline]
}
[any exit code]
.
.
.
[return]
}One thing to note is that as you're drawing, if you watch it in slow-motion, you'll see that you're drawing each scanline from left-to-right, top-down. Nice and clean. I'll address this cool feature later...
[size="3"] Q: "What is...KEY ELEMENT #2: The insertion routine"
Due to the nature of it's possible complexity, the Insertion routine is the most important key element of the s-Buffer algorithm. As such, it's also the most confusing routine to write.
Like some compression routines, any version of the de-compression routine can de-compress the data stored in compressed form. However, each version of the compressing code is different. Better compression can be obtained by better analysis. The format of the output is still the same, but substantial gains can be made by better analysis in the compressing code. I believe that the Insertion routine can also have this trait. A better analysis on the part of the Insertion routine can simplify the job of the low-level drawing routines.
My point is that there is ALWAYS room for improvements to be made to any insertion routine. The closer to perfect elegance, the better.
Take my rudimentary psudo-code for example. The code relies on splitting segments that may not need splitting simply to keep the algorithm simple for explanation's sake. It does the job, but it is wasteful.
Granted, the segments won't overlap (that would defeat the purpose of s-Buffering all together). But on many occasions, a segment may be split into two segments side-by-side, causing the low-level drawing routines more effort, and wasting memory by using up more segments than are necessary. And ultimately more time is spent in the drawing phase.
Please note that the following code may not be satisfactory for real use, but will certainly improve the performance of your application regardless.
You'll need these defined before we can start...
Cur = Start of the existing segment list
New = Segment to be added to the list cccccccc
nnnnn
The Cur's right-half is overlapping with the entire New segment, and an intersection must be tested for. These examples only represent where the start x coordinates and ending X coordinates fall, they in no way represent the depth values.nnnnn
Possible cases:
Case 1:
-> cccccc
-> nnnnnn
Case 2:
-> cccccccc
-> nnnnnnnn
Case 3a:
-> ccccccccc
-> nnnnnnnnn
Case 3b:
-> cccccccccc
-> nnnnnnnnnn
Case 3c:
-> ccccccccc
-> nnnnnnnnnnnnnnnnn
Case 3d:
-> ccccccccccc
-> nnnnnnnnnnnnnnnnn
Case 3e:
-> c
-> nnnnnnnnnnnnn
Case 3f:
-> c
-> nnnnnnnnnnnnn
Case 4a:
-> ccccccccccccc
-> nnnnnnnn
Case 4b:
-> ccccccccccccc
-> nnnnnnnnnnn
Case 4c:
-> ccccccccccccc
-> n
Case 4d:
-> ccccccccccc
-> nnnnnnnnnnn
Case 4e:
-> ccccccc
-> nnnnnnn
Case 5:
-> cccccccccccccc
-> n
Case 6:
-> cccccccccccccc
-> nnnnnnn
Case 7:
-> c
-> nnnnnnnnnnnnn
Case 8:
-> ccccccc
-> nnnnnnnnnnnnnn
Case 9:
-> c
-> n
Case 10:
-> cccccccccccccc
-> nnnnnnnnnnnnnn if (New is entirely off-screen)
return;
// Make sure segment is sorted left-right
if (the list is empty)
{
just add it
}
while(we still have entries in the list)
{
// Case 1
if (New.x1 > Cur.x2)
{
// Next Cur
// Continue Checking
}
// Simply off-screen? (do this check again 'cause New is changin')
else if (New.x1 >= ScreenResX || New.x2 < 0)
{
// Return
}
// Case 2
else if (New.x2 < Cur.x1)
{
// Add New before Cur;
// Return
}
// Case 3
else if (New.x1 < Cur.x1)
{
// Split New at Cur's left-most point
// Add New's left-half before Cur
// Replace New with it's right half
// Continue checking
}
// Case 4
else if (Cur.x1 < New.x1)
{
// Split Cur at New's left-most point
// Add Cur's right-half after Cur
// Next Cur
// Continue checking
}
// Cases 5 & 6
else if (Cur.x2 > New.x2)
{
// Case 5
if (New.x1 == New.x2)
{
// If New's starting Z is behind Cur's starting Z, just return
// Split Cur at New's right-most point + 1
// Replace Cur with it's right half
// Add New before Cur
// Return
}
else
// Case 6
{
// Split Cur at New's right-most point + 1
// Replace Cur with it's right half
// Call IntersectSplit for New and Cur's left-half
// Return
}
}
// Cases 7 & 8
else if (Cur.x2 < New.x2 )
{
// Case 7
if (Cur.x1 == Cur.x2)
{
// Split New at Cur's right-most point + 1
// If Cur is behind New's left-half, replace Cur with New's left-half
// Continue checking using New's right half
}
// Case 8
else
{
// Split New at Cur's right-most point + 1
// Remove Cur from the list
// Call IntersectSplit for Cur and New's left-half
// Continue checking using New's right-half
}
}
// Cases 9 & 10
else
{
// Case 9
if (Cur.x1 == Cur.x2)
{
// If Cur is behind New, replace Cur with New
// Return
}
// Case 10
else
{
// Remove Cur from the list
// Call IntersectSplit for Cur and New
// Return
}
}
}
// Just add it to the end
// ReturnIntersectSplit() simply finds the intersection of two lines that start at the same x coordinate, end at the same x coordinate and returns the order in which the two segments appear from left->right, unless one segment is totally behind the other, in which case it simply returns the single segment.
Note that your splitting code must be very accurate. Not making an accurate splitting routine or an accurate IntersectSplit() routine may cause artifacting in the foreground polygons caused by polygons hidden behind them.
Besides, if your intersection and splitting routines are accurate, then you can expect more accurate results than a 16-bit z-Buffer.
For more information on inserting segments into the list, see the Q titled: "What are some ways to improve the Insertion routine?"
[size="3"] Q: "What is...KEY ELEMENT #3: The segment manager"
The segment manager is simply a reservoir of pre-allocated segment structures. These segment structures hold the actual segments that are linked together in the s-Buffer's linked lists.
If you were to malloc() and free() segments as you needed them, you run the risk of fragmenting memory, and running out of larger chunks of memory for other parts of your application. Not to mention the extra overhead of the malloc() and free() routines.
To solve this problem, a segment manager is needed. It keeps a reservoir of segments, and gives you free segments as you ask for them. This may be done in any number of ways. It's also very fast.
A simple data example would be an array of SEG pointers that is "grown" as needed, in blocks of...say...512 segments at a time. When you run out of available segments, you simply allocate another block, and give one up.
Here's some psudo-code for the GetSegment() routine:
SEG *GetSegment( void )
{
if (there are no available segments)
{
GrowReservoir()
}
Find an available segment
Decrease the number of available segments in the reservoir
Return the segment pointer
}InitSManager()
[bquote]Allocates the default base number of segments for the reservoir probably by calling GrowReservoir()[/bquote]UninitSManager()
[bquote]Frees all memory in use[/bquote]ResetSManager()
[bquote]Marks all segments in reservoir as "available"[/bquote]GetSegment()
[bquote]Find an available segment (call GrowReservoir() if none are available), mark it as used, and return it's pointer.[/bquote]CopySegment()
[bquote]A simple memcpy() will do[/bquote]GrowReservoir()
[bquote]realloc() the reservoir's array of segments in increments of some pre-determined number. Use a #define for this number for fine-tuning memory usage.[/bquote][size="3"]Q: "What are some ways to improve the Insertion routine?"
Now, it's your turn. Let's have some optimizations. I'd love to see any code/psudo-code submissions to the FAQ! Here are some things to consider:
- Using a Binary-searchable tree instead of a linked list
- Checking entire New segments for fully behind or in-front before adding or quitting.
- [this section not complete]
Considering the accuracy of splitting two 2D line segments, the accuracy is perfectly pixel accurate where as a 16-bit z-Buffer is only partially accurate for a 32-bit world coordinate system.
[size="3"] Q: "What kind of performance can I expect?"
I can't say, at this time, exactly what sort of performance improvements to expect over z-Buffer. It all depends on the application, the code used for the segment manager, and especially the insertion routine. When I have some numbers, I'll include them here.
However, let me explain why I believe you can expect better results out of s-Buffering than z-Buffering in hardware. No this dude ain't nuts, that's right, software that's faster than hardware. Keep on readin'.
When you're rendering to the s-Buffer, if you're clever about it in your insertion routine, you can eliminate many segments before they get into the s-Buffer, so you've just eliminated a segment that your code would have spent VERY valuable time drawing. Consider this example:
There are (roughly) 300 pixels in the above example. 200 of which overlap. Using z-Buffering in hardware, you will have to draw 500 pixels, keep in mind that you'll also have to track the z-coords for each pixel for use with the z-buffer hardware. But we'll ignore that fact for now.
So you draw blast out 500 pixels. This is your lowest-level code. This is your fastest stuff.
You've just rendered a full-screen of polygons, and 40% of it was for nothing. Jeesh! 40%! What a waste!
Consider s-Buffers. They immediately find that where you have an overlap in the example, there is no extra drawing to be done. Granted this takes a little time (not much, mind you). But the savings is 40% of screen-space coverage! You're simply NOT drawing those pixels!
There are other advantages, too.
s-Buffers allow you to cut your drawing to the significant pixels ONLY. You draw 300 pixels (without tracking the z-coord along the way).
Unless the hardware is drawing the stuff for you (which s-Buffers should be nicely adaptable to -- if the hardware supports scanline drawing of textures, shades, etc. rather than entire polygons) then you're still doing the drawing. The z-Buffer hardware is only helping you out with your low-level code. It's only doing something for you. It's not reducing the number of pixels you draw, it's just doing some work for you.
s-Buffers not only reduce your workload by reducing the amount of screen space coverage you're drawing to, but it does the z-Buffering for you. Just like hardware does. Granted there is overhead for inserting segments, but nothing compared to the rendering of them to the screen only to find that they're not viewed.
So, in this example, you see about a 5/3 speed improvement. It gets much better as you have more hidden polygons. But, with z-Buffering, your performance just plummets with more hidden polys. It's an inverse non-linear scale to your disadvantage.
[size="3"] Q: "Yeah, so like, what about memory?"
Since you've written a segment manager (which is, by definition -- a memory manager) you've got control. You decide how much memory to allocate at any one point in time. The smarter your segment manager is the better off you'll be.
But there is still the issue of how much memory to store the required segments in the list.
For simple gouraud shading, here's what I would expect a segment structure to look like:
typedef struct segment
{
short start_x, end_x; // starting and ending Xs
short start_z, end_z; // starting and ending Zs
char start_s, end_s; // starting and ending shade values
} SEG;This does NOT include any inefficiencies in your segment manager or insertion routine (see the insertion routine questions for details).
You may not be doing simple grayscale gouraud shading. You might have colors, too. Add a byte (or whatever your app requires) for color.
Then there's the texture mapping information. This adds to the size, too -- possibly almost doubling the amount of memory required. But in some games (especially Wolfenstien-style games), you can still find a tremendous memory advantage over z-Buffers since the segments will most likely be so long.
These are things to consider when using s-Buffers. If you find that the s-Buffers will use more memory than z-Buffers, you've got a decision to make: Speed or Memory?
[size="3"] Q: "What are some more possible advantages of s-Buffers?"
As you render the s-Buffer, you'll be rendering the screen top-down, and each scanline from left to right. I can't think of any obvious advantages this offers other than the fact that it makes your low-level drawing routine a tightly optimized muscle machine.
If you have any cool ideas to make use of this unique feature, please lemme have 'em!
It would be an easy task to add information to your s-buffer lists that allows you to determine which scanlines have changed since the previous render so that your screen updates only contain updates to the scanlines that have changed. This will reduce the amount of time you spend updating the slow RAM on your video card (for PCs).
For more, see the next two sections on Masking and Transparencies.
[size="3"] Q: "What about masking?"
Many games have dash-board masks or the like. s-Buffers offer a clean way to handle this.
You can add a flag to your segment structures that can make it a masking segment.
This way, you can build a masking s-Buffer, use it as your starting point when you render, and insert segments into it, not letting them interfere with the masking segments. This will remove the need to perform pixel-by-pixel masking as the image is drawn to the screen.
This will also prevent your low-level drawing routines from having to render pixels behind the mask.
[size="3"] Q: "What about transparencies?"
By extending the masking idea a bit further, you can flag certain segments as transparent. As you insert segments, any non-transparent segments that fall behind the transparent ones won't remove the transparent segments. Any non-transparent segments that end up in-front of the transparent ones will clip the transparent segments.
This brings up the problem that some segments now overlap with transparent segments, making the Insertion routine that much more complex.
Note that transparencies modify the image behind them. If these transparent segments are kept in order of left-right (following their non-transparent neighbors in back-front order) within the linked-list for a scanline, as the low-level drawing routine draws the transparent segments, the non-transparent ones will already have been drawn, and the transparency modifications will fall into place nicely.
[size="3"]
Q: "What are the disadvantages?"
If s-Buffers are used to store many small segments, of if you use an inefficient Insertion routine, you might find that the memory requirements will be quite high. I would expect that this would only be a concern in a small percentage of the applications out there.
There can be much difficulty in writing the insertion routine.
s-Buffers won't work with some implementations of curved surfaces as a z-Buffer will.