This is going to be a tutorial on how to put together a simple 3d engine. It assumes you already know a bit of Glide and MSVC++ programming but you don't have to be a diehard professional. You just need to know the basics. I'll assume you already have your Glide SDK running and you can compile some simple Glide-programs.

setup.zip is a little program to setup and close your Glide programs. The code in the tutorial was written for Glide but most of it can easily be used for any other system like OpenGL or DirectX.

We'll take a look at a couple of problems:

1. Making an Object structure
2. Loading an Object in to your structure using 3DS .ASC files
3. Rotating an Object
4. Gouraud shading our Object
5. And loading and displaying TGA files

I just want to make one more statement. Many of the things I write may not be very elegant code and I know that most things can be done far more efficient but I'm a starter, just like most of you. This is the way I managed to do certain things. If you have any comment on how to improve my program's please let me know.


[size="5"]Making An Object Structure

The Object structure is a structure in which we will keep information concerning a specific object, like shape, color, position, etc. First we should know which information we need to save in our structure. We'll need at least the Vertex en Faces information and maybe we could use some sort of object id number. We'll also need to save our 2d 'screen' coordinates. Let's split up our problem and fist take a look at how to save a single vertex. Take a good look at structs1.zip to see that I mean.

Next we do this for every datatype we need. These can be Faces, Normals, 2d and 3d coordinates, etc. When completed I could look something like structs2.zip.

Now we can simply define a Object structure. I use pointers in the object structure because we don't know the number of vertices and/or faces in advance. By using pointer we can just load a file in memory and then make the pointer to point to the information in memory. The whole file should look something like structs3.zip


[size="5"]Loading An Object Into Your Structure Using 3DS .ASC Files

Now starts the fun part, loading you own 3d files. Let's have a look at this so called .ASC fileformat. A sample of such a file is located in sample.zip

.ASC files can be generated using 3DStudio (if anybody knows any other piece of software which exports this format, please let me know !) but free ascfiles can be found all over the web.

As you can see the file starts with the Ambient light color. For now we can just skip this. After that follows objectname, number of vertices and number of faces. This is the first information we need to know. We will use fgets and fscans to read a line at a time. We can excess the file using the following code:

Now the only thing that remains is reading our vertices and faces. But before we can do that we must make a local pointer and reserve memory for this info.

The whole loadroutine could look something like this:

Note:

• This routine does a few other things besides just loading an object in memory. It can take a scale factor as argument. This scalefactor is used to scale the object when it is loaded. This is simply done by lust multiplying all vertices with the scale factor.
• fscanf could be used is many cases which would have resulted in cleaner code, but for some reason it just didn't work! Any ideas?
• I use a command called PrecomputeVertexNormals(...). This may seem useless at this time as there is no such function but it is used if gouraud shading is enabled. I'll get to this function when talking about gouraud shading.
• The function ReadTil(string) reads on till the string is found. Most asc files contain pagenumbering, so if we always just go to the next line we will get in trouble. ReadTil() is defined like this:
  
  
  #define ReadTil(string) while(strcmp(line, string)) fscanf(fp, "%s", line);
  
  [size="5"]Rotating An Object
  
  Now I'll be explaining just the minimal you'll be needing to know about 3d rotation. If your serious about coding 3d you should get yourself a book. A good startingpoint would be The Black Art of 3d Game Programming. It is written for dos and uses old technique's but it's illustrates the problems well.
  
  

  

  
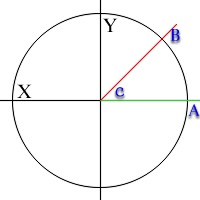
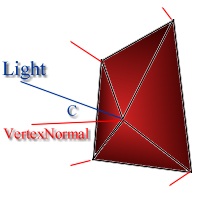
  If we want to rotate an object in three dimensions we first have to look how we're going rotate an object in two dimensions, as this is almost the same problem but if we want it in 3d we must do it over three angles instead of one. Take for example the figure shown here and we want to rotate point A to point B. The rotation angle is now C. Normally we would do something like this:
  
  
  Xnew = COS( C ) * Xold
Ynew = SIN( C ) * Yold
  
  But this only works if C is the angle calculated from the horizontal line. If we want to work around this problem we will need to change our calculation in to:
  
  
  Xnew = COS( C ) * Xold - SIN( C ) * Yold
Ynew = SIN( C ) * Xold + COS( C ) * Yold
  By now we have rotated one point over one angle in one direction. The next thing to do is just repeating this principle in all direction X, Y and Z. A MSVC++ code version could look like this:
  
  
  void RotateObject(D3Object_ptr Object, int angleX, int angleY, int angleZ)
{
float temp_x, temp_y, temp_z;
int count;

for(count=0; count < Object->NumVertices; count++)
{
temp_x = c[angleX] * Object->Vertices_local[count].x - s[angleX] * Object->Vertices_local[count].y;
temp_y = s[angleX] * Object->Vertices_local[count].x + c[angleX] * Object->Vertices_local[count].y;

Object->Vertices_world[count].x = c[angleY] * temp_x - s[angleY] * Object->Vertices_local[count].z;
temp_z = s[angleY] * temp_x + c[angleY] * Object->Vertices_local[count].z;

Object->Vertices_world[count].y = c[angleZ] * temp_y - s[angleZ] * temp_z;
Object->Vertices_world[count].z = c[angleZ] * temp_z + s[angleZ] * temp_y;
}
}
  As I said this is the absolute minimal you need to know if you want to create a 3d program for your self. Please refer to some good books if you want to know more.
  
  
  [size="5"]Gouraud Shading Our Object
  
  Let's see... We now have our Object loaded, rotated and we could easily render it to screen. Just divide every X and Y by its Z (the further the point is the bigger Z, so the point is divided by a bigger value resulting in points that are closer to the origin (which should be at the center of the screen) if they are further away from the camera. But if you didn't use any color in your polygons it is going to look really awful. Let lighten this up a little bit.
  
  Let me start with flat shading. If we flat shade an object we calculate the normal of a face, calculate the angle between the lightsource and the face normal and use this angle as an indication of the amount of light that hits this face. See the following pictures to illustrate this.
  
  

  

  
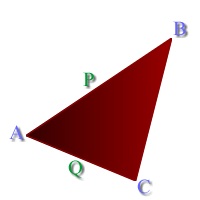
  We can calculate a normal using the following formula. Let us assume we know the vectors AB (P.x, P.y, P.z) and AC (Q.x, Q.y, Q.z). The normalvector now has the following components.
  
  N.x = ( ( Q.y * P.z ) - ( Q.z * P.y ))
N.y = ( ( Q.z * P.x ) - ( Q.x * P.z ))
N.z = ( ( Q.x * Py ) - ( Q.y * P.x ))
  

  

  
  To calculate P and Q use the this: Let us assume B and C are to coordinates with are not in the origin and we would want to know the vector BC. To get the components of BC just subtract all the B components from the C components. This would make:
  
  
  P.x = B.x - A.x
P.y = B.y - A.y ... etc (this also counts for Q)
  We now can calculate the angle C between the lightsource and the normal of the face.
  
  
  LengthOfNormal = SQRT(( N.x * N.x ) + ( N.y * N.y ) + ( N.z * N.z ))
LengthOfLight = SQRT(( Light.x * Light.x ) + (Light.y * Light.y ) + ( Light.z * Light.z))
Angle = ACOS(( N.x * Light.x )+( N.y * Light.y )+( N.z * Light.z )) / ( LengthOfNormal * LengthOfLight)
  
  

  

  
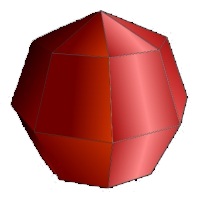
  Now use the Angle to scale all color components R,G and B of the face. All this should result into an object looking something like shown left. All the calculation stay the same if we go on to gouraud shading. The only difference in we don't use the facenormals but we calculate vertexnormals.
  
  Just figure out which faces share a vertex. Then calculate the normals of these faces, add them and divide them by the same number of faces.
  
  

  [nbsp][nbsp][nbsp][nbsp]

  
  Calculate the angle C between the Light and the Vertexnormal as we did with flat shading and again use it to scale the colorcomponents of the vertex. The picture left is an example of how it could look... not such a good one but that is because it is handdraw.
  
  Simple..huh?
  
  Well, I skipped some details. One such is we must do the calculation of the vertexnormals in advance and save them in memory to decrease the number of calculation we have to do in real-time.
  
  The sourcecode for recalculating the vertexnormals, calculating the angle between the lightsource and the vertexnormal and scaling the colorcomponents can be found in gouraud.zip.
  
  
  [size="5"]Loading And Displaying TGA Files
  
  This part of the tutorial has nothing to do with 3d programming, but if you are creating a game or any other application you will sometimes have to use static ( non 3 dimensional ) screens. These are almost always just simple pictures that fill the whole screen. I will show you how you can load a TGA picture directly on screen and how you can load an TGA in to memory and then copy it to the screen using grLfbWriteRegion(). All TGA routines I describe only work with UNCOMPRESSED TGA!
  
  Loading a uncompressed TGA is very simple. Skip the first 18 bytes, then read all the pixelsvalues as RGB (one byte each). That means if we read a screen of 640 x 480 we need to read 640*480*3 bytes = 921600 bytes. Look at loadtga.zip to see an example source