Writing Fast Code: Introduction To Algorithms and Big-O
Comments


Who is this written for? Do professional developers need this help or is this for folk trying to break into the industry?

@colonycapture This will benefit anyone who wants an introduction to Algorithms and Big-O. This may include professional developers who have not taken this in a university setting (e.g. self-taught) or a beginner.

Efficient way of searching a weakly ordered 2D array in at worst linear time: http://www.cs.geneseo.edu/~baldwin/math-thinking/saddleback.html

Thank you for this, we're doing an algorithm course at my university atm and this is exactly what we're learning about, however, I find your examples and explanations much more easy to understand. You're a life saver!




Thanks a ton to get me started on algorithms, very well written , descriptive with nice example with less technical jargon.

Who is this written for? Do professional developers need this help or is this for folk trying to break into the industry?
I was completely unaware of this kind of stuff until I entered university, so I suspect it will cover a blank hole for many self-taught programmers (and I'm sure you'll agree with me the subject is hugely important). I wrote more than a couple of bubble sorts in my earlier years due to ignorance :)

Where's the second half of the article? It cuts off right when it's about to get to the good stuff! It doesn't mention that mergesort is O(n log n), which IIRC is the theoretical optimum for sorting algorithms (and it's pretty interesting to implement, too). Then it might bring up space considerations and sorting stability, which can also be important depending on the situation, and compare with heapsort (though that might be confusing since it's not really divide-and-conquer). Then it might discuss how randomization can turn quicksort, an O(n^2) algorithm, into an algorithm that often performs better than most O(n log n) algorithms in practice.
That would make a more complete intro on writing fast (and good?) algorithms, at a minimum. At the risk of making it even more of an article about sorting, it might link a few hybrid algorithms and discuss how popular languages/libraries implement their sorting algorithms, e.g. python and Java 7 use timsort (hybrid of mergesort and insertion sort), and g++ uses a hybrid of introsort (which is itself a hybrid of quicksort and heapsort) and insertion sort. That would be a good time to remind people to not reinvent the wheel when it's not necessary, since in most languages it's easier, faster, and almost certainly less error prone to tell the built-in algorithms how to handle your game's objects rather than writing your own algorithms.



This is the tip of the tip of the iceberg. If you want to get a really good reference and resource for all things concerning algorithms, I strongly recommend getting this book:
http://mitpress.mit.edu/books/introduction-algorithms
One thing I'll say about books: They cost money, but they are much more thorough and deep than any collection of articles you could ever hope to find on the internet. IMHO, They're well worth the investment.
The other book I strongly recommend: http://www.amazon.com/Mathematics-Programming-Computer-Graphics-Edition/dp/1435458869
This book deals with all of the advanced mathematics and concepts related to computer graphics programming. Choosing the right datastructure/algorithm is half the battle, having a good conceptual background and the supporting mathematical tools at your disposal is the other half. This book is somewhat terse with its explanations, but I've found it to be quite a valuable resource for filling in the gaps in my knowledge.

@Imelior & @slayemin You guys are totally correct. Rereading my article, I have the same thoughts as you guys. I guess I cut it off like that because it was getting pretty lengthy. But still...

I am glad you added the
Note: That little tidbit about computers doing repeated addition is a bit of a lie.
Because thats not quite exactly how a decent algorithm or computer would implement it.
Overall decent article.
Notes:
Should add the O notation to help better reinforce when you are talking about it, such as the case of O(n^2) is to signify the notation and difference.
Also, you should double check your greek letters, omega, theta, etc... and which one is best/worst because you have at least one instance mixed up backwards...

Yeah, one thing that should be mentioned about O notation is that it can be a bit of a trap. O notation is useful for large datasets, but because it drops constants and even constant multipliers, it can be misleading when dealing with games. Games often have fairly small datasets, so two custom algorithms that are both O(n), but in reality O(3n) and O(n + 1000) can actually make for a fairly big performance difference for a game.
I'm not saying Big O is useless, but that a developer should make sure they don't fall into a trap of always using the algorithm with the best O notation, without looking at their dataset size and their average usage scenario. (as well as worst and best case and how often those two cases actually come up)

I like how this is written. Also it can be very important to anyone really just getting into Computer Science at a University. This will be one of the first classes a Computer Science major would take so I do find it wise for someone to know the basics of Big O. You'd also be studying these sorting algorithms for the most part early in the class.




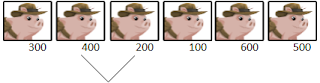
Did you know computers are stupid machines? They are actually so stupid that they don't know how to multiply; instead, they add - whenever you say 2*5, the computer is really doing 2+2+2+2+2!
Just thought it should be point out that this isn't at all what computers are really doing. They do know how to multiply and generally do long (or partial product, or something even more clever perhaps) multiplication (and division) pretty much like any person would. Please forgive me if you correct this later in the article and I missed it, but it seems a pretty glaring oversight given the subject matter.
Would have made a good example of the classic teaching mechanism of "What I told you earlier isn't entirely true..." to reveal how computers actually use much more clever algorithms and the binary long multiplication is in fact surprisingly trivial.

Did you know computers are stupid machines? They are actually so stupid that they don't know how to multiply; instead, they add - whenever you say 2*5, the computer is really doing 2+2+2+2+2!
Just thought it should be point out that this isn't at all what computers are really doing. They do know how to multiply and generally do long (or partial product, or something even more clever perhaps) multiplication (and division) pretty much like any person would. Please forgive me if you correct this later in the article and I missed it, but it seems a pretty glaring oversight given the subject matter.
Would have made a good example of the classic teaching mechanism of "What I told you earlier isn't entirely true..." to reveal how computers actually use much more clever algorithms and the binary long multiplication is in fact surprisingly trivial.
Agreed, in fact in this particular example one would hope that the compiler would know to replace any *2^n with a shift n left




Ever wondered what makes code fast? Here we take a look at different algorithms, their running time, and Big-O.



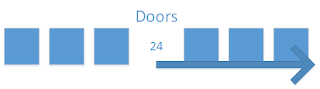
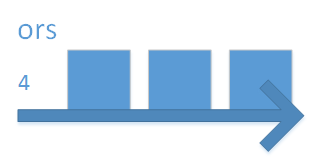
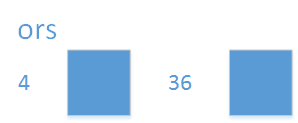







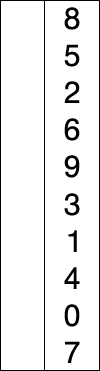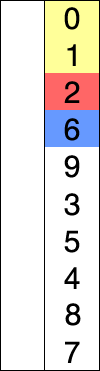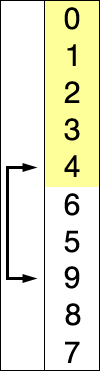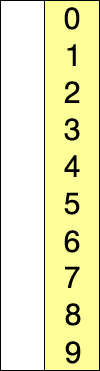



Very Nice.