Collision detection is an area of game development that scares most into using third party physics APIs due to its seemingly vertically-steep learning curve. Most programmers understand the axis-aligned bounding box (AABB) algorithm but have trouble transitioning to the more difficult algorithms such as SAT and GJK. Swept AABB is the middle player that will show a lot of the problems that can occur with normal AABB and help understand core concepts used in more advanced collision techniques.
This article assumes you understand the AABB algorithm. There is also a bit of vector math, but it won't get overly complicated. Examples are done in C/C++ but can be easily converted to other languages. At the end, I have given source files for C/C++ and C#.
What is Swept?
AABB has a major fundamental problem that may not be visible at first. Take these 3 examples:
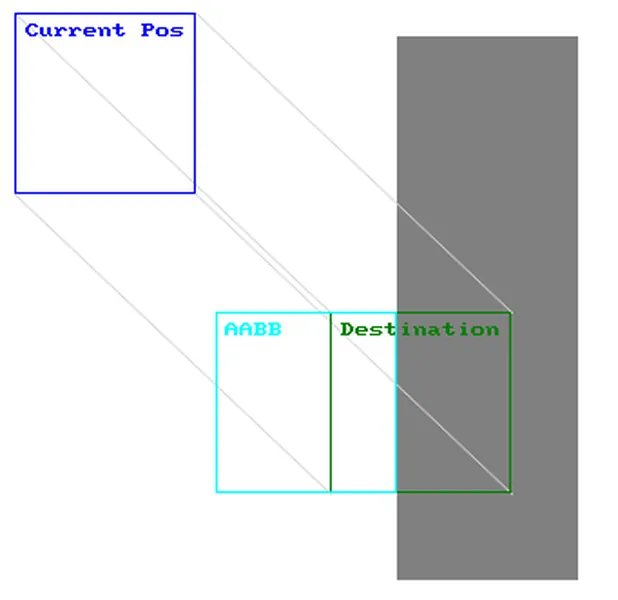
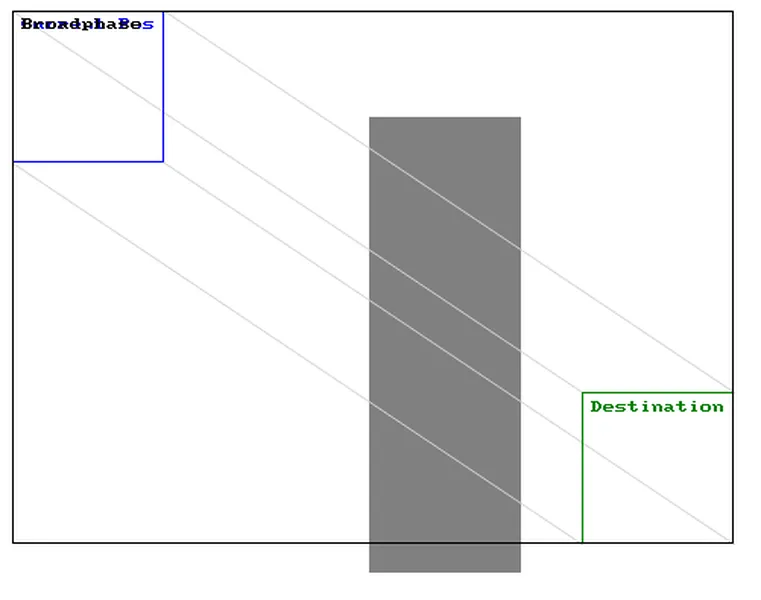
Example 1: A normal AABB collision. The blue box is where the box is at the beginning of the frame. The green box is where the box is expected to be by the end of the frame. The aqua box shows where AABB will place the box after collision. The gray box is a static (unmovable) block that is tested for collision. This shows a normal collision. The box is moved to the nearest point that is not a collision. This is fine and is the expected result of AABB.
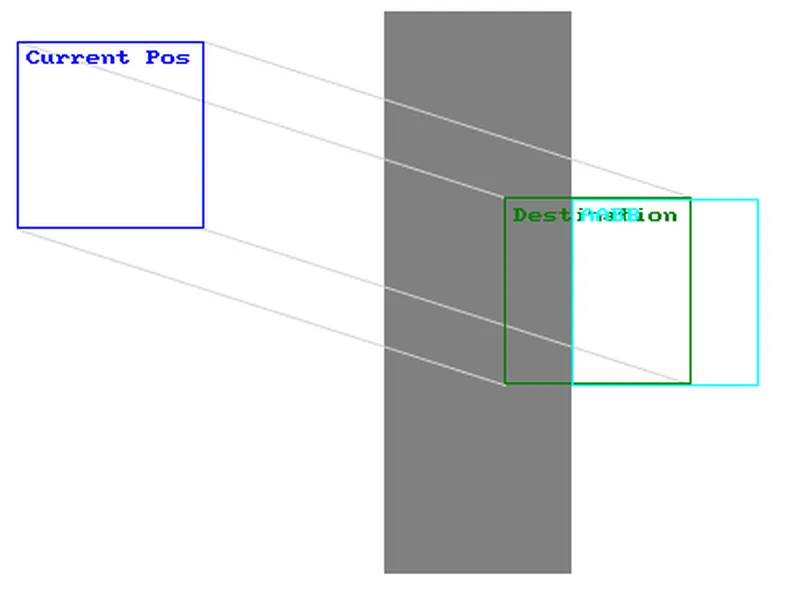
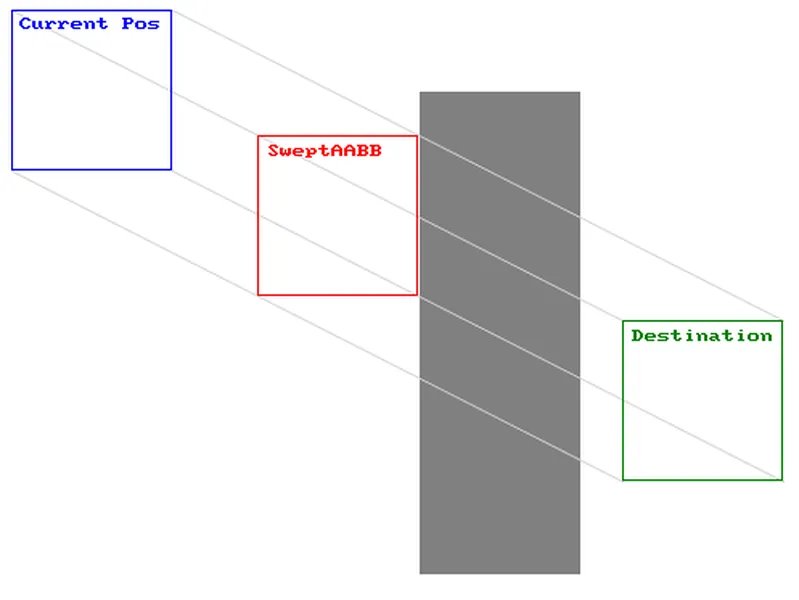
Example 2 shows a similar collision where the destination is further on the opposite side. As you can see, AABB has placed the response box on the opposite side of the block. Logically, this makes no sense as it has magically passed through the object.
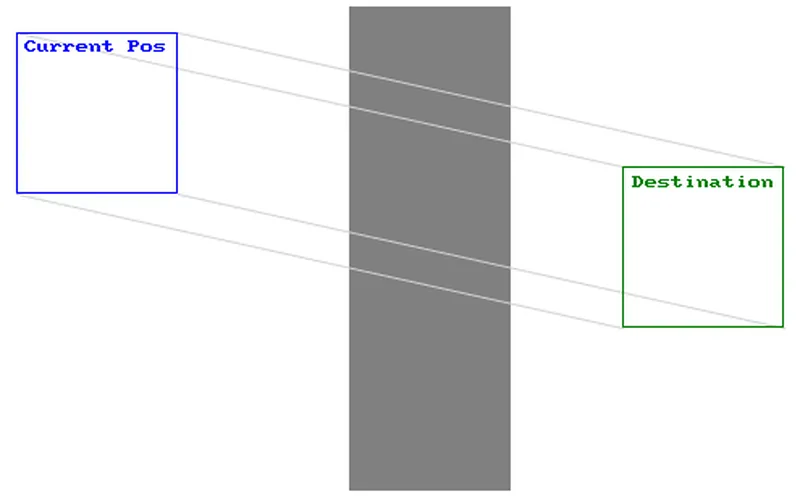
Example 3 shows a destination that doesn't collide with the object. AABB will assume that there was no collision and the moving box will move through it like there was no collision at all. So when do these problems occur? These problems usually appear when objects are moving fast and/or the program is running at a low frame rate. To avoid this, we need to somehow predict where the box travelled between each frame. This concept is called swept.
Implementing Swept AABB
In this implementation, we will assume that a box is defined by a position at the top-left corner of the box and a width and height. Now that we are taking swept into consideration, we also need to remember the velocity.
The velocity of an object is how far the object will move per second. If we multiply the velocity by the delta time, you will have the displacement that the object must move in this frame.
So we will define our box like so:
// describes an axis-aligned rectangle with a velocity
struct Box
{
// position of top-left corner
float x, y;
// dimensions
float w, h;
// velocity
float vx, vy;
};
vx and vy refer to the velocities, w and h are the box dimensions. The function that will perform the test will look like this:
float SweptAABB(Box b1, Box b2, float& normalx, float& normaly)
The first parameter is the box that is moving. The second is the static box that will be tested against. The last two parameters make up the normal of the collided surface. This will be used later on when we want to respond to the collision.
A normal is the direction that an edge of an object is facing. Think of a perpendicular arrow pointing away from face at 90 degrees.
The return value is a number between 0 and 1 that indicates when the collision occurred. A value of 0 indicates the start of the movement and 1 indicates the end. If we get a value of 1, we can assume that there was no collision. A value of 0.5 means that the collision occurred halfway through the frame. This will also be used later to respond to the collision.
Now, to first start the algorithm, we need to find the distance and time that it takes to reach a collision on each axis.
float xInvEntry, yInvEntry;
float xInvExit, yInvExit;
// find the distance between the objects on the near and far sides for both x and y
if (b1.vx > 0.0f)
{
xInvEntry = b2.x - (b1.x + b1.w);
xInvExit = (b2.x + b2.w) - b1.x;
}
else
{
xInvEntry = (b2.x + b2.w) - b1.x;
xInvExit = b2.x - (b1.x + b1.w);
}
if (b1.vy > 0.0f)
{
yInvEntry = b2.y - (b1.y + b1.h);
yInvExit = (b2.y + b2.h) - b1.y;
}
else
{
yInvEntry = (b2.y + b2.h) - b1.y;
yInvExit = b2.y - (b1.y + b1.h);
}
xInvEntry and yInvEntry both specify how far away the closest edges of the objects are from each other. xInvExit and yInvExit is the distance to the far side of the object. You can think of this is a being like shooting through an object; the entry point is where the bullet goes through, and the exit point is where it exits from the other side. These values are the inverse time until it hits the other object on the axis. We will now use these values to take the velocity into account.
// find time of collision and time of leaving for each axis (if statement is to prevent divide by zero)
float xEntry, yEntry;
float xExit, yExit;
if (b1.vx == 0.0f)
{
xEntry = -std::numeric_limits::infinity();
xExit = std::numeric_limits::infinity();
}
else
{
xEntry = xInvEntry / b1.vx;
xExit = xInvExit / b1.vx;
}
if (b1.vy == 0.0f)
{
yEntry = -std::numeric_limits::infinity();
yExit = std::numeric_limits::infinity();
}
else
{
yEntry = yInvEntry / b1.vy;
yExit = yInvExit / b1.vy;
}
What we are doing here is dividing the xEntry, yEntry, xExit and yExit by the object's velocity. Of course, if the velocity is zero on any axis, it will cause a divide-by-zero error. These new variables will give us our value between 0 and 1 of when each collision occurred on each axis. The next step is to find which axis collided first.
// find the earliest/latest times of collisionfloat
entryTime = std::max(xEntry, yEntry);
float exitTime = std::min(xExit, yExit);
entryTime will tell use when the collision first occurred and exitTime will tell us when it exited the object from the other side. This can be useful for certain effects, but at the moment, we just need it to calculate if a collision occurred at all.
// if there was no collision
if (entryTime > exitTime || xEntry < 0.0f && yEntry < 0.0f || xEntry > 1.0f || yEntry > 1.0f)
{
normalx = 0.0f;
normaly = 0.0f;
return 1.0f;
}
The if statement checks to see if there was a collision or not. If the collision time was not within 0 and 1, then obviously there was no collision during this frame. Also, the time when the collision first entered should never be after when it exited out the other side. This is checked, and if it failed, then we assume that there was no collision. We specify 1 to indicate that there was no collision. If there was a collision, our last step is to calculate the normal of the edge that was collided with.
else // if there was a collision
{
// calculate normal of collided surface
if (xEntry > yEntry)
{
if (xInvEntry < 0.0f)
{
normalx = 1.0f;
normaly = 0.0f;
}
else
{
normalx = -1.0f;
normaly = 0.0f;
}
}
else
{
if (yInvEntry < 0.0f)
{
normalx = 0.0f;
normaly = 1.0f;
}
else
{
normalx = 0.0f;
normaly = -1.0f;
}
} // return the time of collisionreturn entryTime;
}
Since all of our boxes are axis-aligned, we can assume that there are only 4 possible normals (one for each edge of the box). This simple test will figure that out and then return the collision entry time. This is all of the code we will use for swept AABB but it won't work correctly in certain cases! That is because we need to implement broadphase (we will cover this soon). But, for now, there is a whole other step in a collision, and that is the response.
Responses
A collision response is how we want the object to behave after a collision. Before going into some of the different types of responses, we need to figure out the new point where the collision occurred. This should be easy now that we have our swept AABB function.
float normalx, normaly;
float collisiontime = SweptAABB(box, block, out normalx, out normaly);
box.x += box.vx * collisiontime;
box.y += box.vy * collisiontime;
float remainingtime = 1.0f - collisiontime;
Doing 1.0f - collisiontime will give us the remaining time left in this frame (0 to 1 value again). This will perform the collision correctly and might be enough for some uses. But if you try to move the box diagonally into the object ("hugging the wall") then you'll find that you can't move. The moving box will not move at all. This is where the different responses can help.
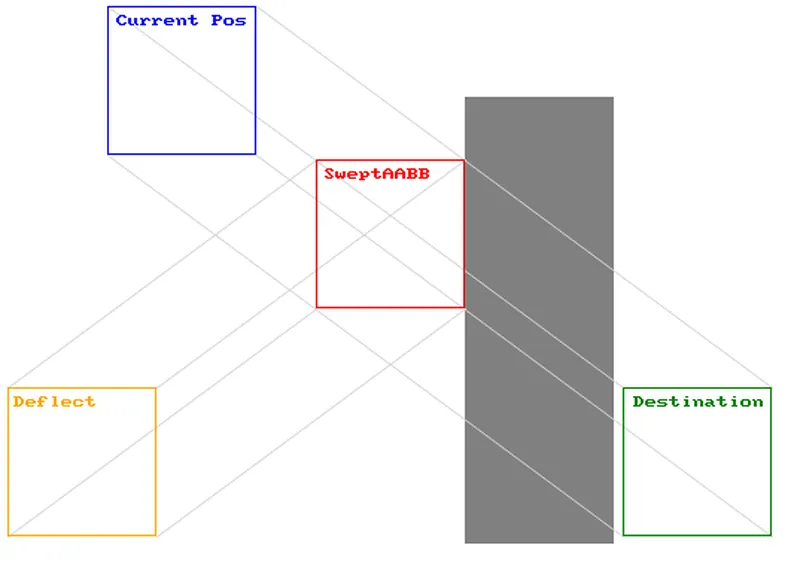
Deflecting
This is most common in games like pong where there is a ball that bounces off objects.
You will notice that when the objects collide, the moving object still has some velocity left in it. What will happen is that the remaining velocity will be reused to move it in the opposite direction, creating a bounce-like effect.
deflectbox.vx *= remainingtime;
box.vy *= remainingtime;
if (abs(normalx) > 0.0001f) box.vx = -box.vx;
if (abs(normaly) > 0.0001f) box.vy = -box.vy;
First we are reducing the velocity by our remaining time. Then we negate the velocity on whichever axis there was a collision. Pretty simple.
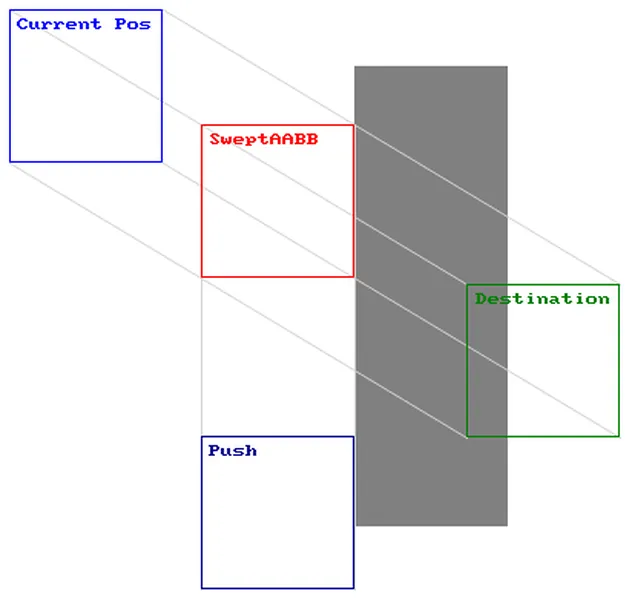
Push
Pushing is more of the traditional "wall hugging" concept where if you run towards a wall on an angle, you will slide along the wall.
// push
float magnitude = sqrt((box.vx * box.vx + box.vy * box.vy)) * remainingtime;
float dotprod = box.vx * normaly + box.vy * normalx;
if (dotprod > 0.0f) dotprod = 1.0f;
else if (dotprod < 0.0f) dotprod = -1.0f;
NewBox.vx = dotprod * normaly * magnitude;
NewBox.vy = dotprod * normalx * magnitude;
It reuses the remaining velocity and pushes it in the direction that is parallel to the collided edge. The first step is to calculate the magnitude of the velocity (this is a programmer version of the Pythagorean Theorem). The next step is performing the dot product with the velocity and the normal of the collided face. We must then normalize this scalar (because we are going to set our own distance). The final step is to multiply the normalized dot product, the switched normal and the magnitude. Alternatively, you could normalize the velocity after calculating the magnitude, so then you don't have to normalize dotprod.
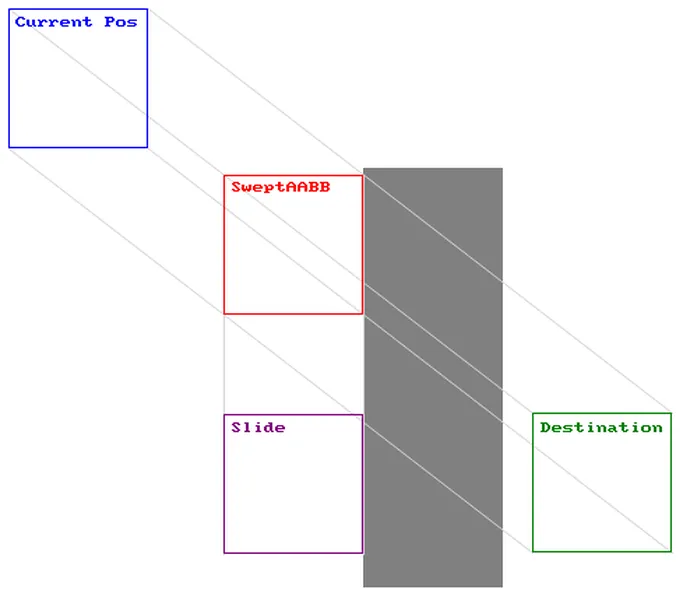
Slide
The problem with the push technique is that it may push the object along faster than expected. A more realistic approach is to do sliding.
This uses vector projection to find the equivalent position on the edge. This is a simpler approach than the push method.
// slide
float dotprod = (box.vx * normaly + box.vy * normalx) * remainingtime;
NewBox.vx = dotprod * normaly; NewBox.vy = dotprod * normalx;
The first thing to remember is that we are swapping the normals around (swap x value with y value). We calculate the dot product, multiply it by the magnitude, and finally multiply it by the swapped normal value. And now we should have our projected velocity.
Broad-Phasing
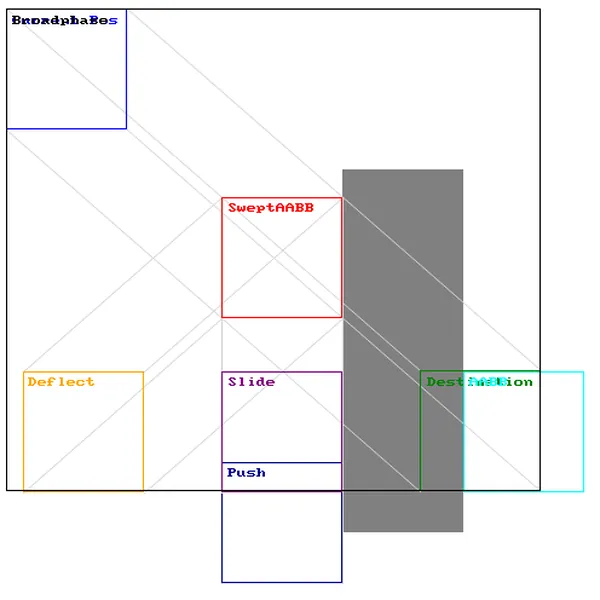
The swept AABB algorithm runs pretty fast, but as more objects come into play, the performance will drop rapidly. A way to combat this is called broad-phasing. This is where you can do a faster, less accurate test to quickly determine if there isn't a collision. There are a few techniques to do this (such as circular distance) but, because our objects are all axis-aligned boxes, it makes sense to use a box again.
The black box around the outside shows us the broad-phase area. This is a box that we can perform a simple AABB test to check if there is a collision or not. Looking at the image, it is safe to say that if an object is not in this broad-phase area, it will not collide with the object. But just because it is within the broad-phase area, does not indicate that there is a collision. If there is a collision with the broad-phase area, we know that we should perform the swept AABB check to get a more precise answer.
Box GetSweptBroadphaseBox(Box b)
{
Box broadphasebox;
broadphasebox.x = b.vx > 0 ? b.x : b.x + b.vx;
broadphasebox.y = b.vy > 0 ? b.y : b.y + b.vy;
broadphasebox.w = b.vx > 0 ? b.vx + b.w : b.w - b.vx;
broadphasebox.h = b.vy > 0 ? b.vy + b.h : b.h - b.vy;
return broadphasebox;
}
This first step is to calculate the broad-phase area. As bad as this looks, all it is doing is adding the velocity to the edge (depending on the direction of the velocity). Now all we have to do is a generic AABB test.
bool AABBCheck(Box b1, Box b2)
{
return !(b1.x + b1.w < b2.x || b1.x > b2.x + b2.w || b1.y + b1.h < b2.y || b1.y > b2.y + b2.h);
}
This is a rather simplified function that returns true if a collision occurred. Now we should be able to put all of the pieces together like this:
// box is the moving box
// block is the static box
Box broadphasebox = GetSweptBroadphaseBox(box);
if (AABBCheck(broadphasebox, block))
{
float normalx, normaly;
float collisiontime = SweptAABB(box, block, out normalx, out normaly);
box.x += box.vx * collisiontime;
box.y += box.vy * collisiontime;
if (collisiontime < 1.0f)
{
// perform response here
}
}
Limitations
The implementation described here has some limitations that you may have figured out already. These include:
- Doesn't take resizing into consideration (i.e. if a box resizes throughout the frame).
- Only allows linear movement. If your moving box is moving in a circular fashion, it will not check where it was extended out on the curve.
- Only allows one box to be moving (i.e. if two boxes move towards each other and collide). This is something I intentionally left out as it starts to involve many of the physics concepts like mass and force.
- It is still only square shapes! You can't even rotate them! This is obvious because the name of the algorithm sort of says that already. But if you have conquered swept AABB, then you might be ready to move onto the next level (like SAT or GJK).
- It is made for 2D only. Luckily, it is quite easy to convert this code to 3D. So long as you understand the concept well, you shouldn't have much trouble with it. I kept it as 2D to keep things as simple as possible.
Code
All of the C/C++ code specified in this article is available for download here. I have also implemented it in C#. This example code will not run a demonstration; it shows only the functions involved. And, just for the hell of it, here's a picture of everything in action:








Excellent tutorial!
Thank you for this contribution,
can't wait to implement this in my own project!