[/font] [font="Arial"][size="2"]
When writing a real time 3d graphics engine the first thing that you should do is decide exactly what is required of the system, particularly if the engine is for game. The next question you should ask yourself is "how can I cheat this?". When I was given the original concept for the landscape engine I most recently wrote it was immediately apparent that the view point would not be required to tilt to any significant degree. The nature of a landscape obviously allows many simplifications in scene management that are not possible with a more general purpose scene management system. When rendering a landscape we always know that we are dealing with a continuous surface that stretches out in all directions. This document is incomplete so far as describing all of the intricacies of developing a fully fledged 3d engine, there are always complexities and implementation specific cases that must be dealt with. Rather this document covers the main design issues giving the reader a good background knowledge on what I did and how I did it.
[size="5"] Restrictions
This is a list of all the restrictions that I considered reasonable to impose on the level structure and camera system within the engine, not all the possible restrictions were actually used but it is important to know what you can and cannot get away with. If you work within the industry for someone other than yourself it might be a good idea to check the list you make with whoever makes the decisions, John Carmack would not have been a happy man if he spend six months writing the DOOM engine only to have his boss say he wants six degrees of freedom! (John Carmack of course does not have a boss, he can afford to do what he wants regardless, I'm jealous, you can tell!)
- Over hangs are not required so scene data comprises of a grid of evenly spaced points called a height map, this makes scene management so easy its unbelievable.
- It is not necessary to be able to tilt the camera.
- [size="2"] The camera is external under control from the user indirectly and can be moved to avoid getting too close to the landscape.
Before I describe how the landscape is actually drawn it is probably best if I describe the basics of linear texture mapping (apologies to anyone who considers this an insult). A triangle is made up of 3 vertices and 3 edges. At each of the vertices we have values that require interpolation with the minimum being U and V co-ordinates into the texture. The U and V co-ordinate pairs essentially describe a triangular area on the texture map that is mapped onto the triangle that is displayed on screen. We map the texture by stepping down the left and right edge of the triangle calculating the appropriate value for U and V at each point then stepping across the horizontal line in a similar manner using the resulting U and V values to index the texture map in order to establish the colour that we need to write to the frame buffer. Lighting or other effects will usually be applied before writing to the frame buffer.
If you evaluate triangle texture mapping with respect to a landscape it starts to become clear that we are performing edge scanning where it is not necessary, that is if we render two triangles together with a shared edge then we are scanning and performing interpolation on the shared edge twice, since we have established that the landscape represents a continuous surface then this totals up to a lot of waste.
[size="5"] My Solution
The algorithm presented here is one I originally conceived during the summer of 95 between finishing university and starting work at SCI. At the time I was working on a Game engine with my good buddy Richard Matthias. The Game Engine was to be a reworked version of the engine I wrote as part of my degree dissertation.
The first step is to determine which axis of the height field best matches the horizontal axis on the screen, this can be done quite simply by checking the camera's At-Vector to see which out of the X and Z component (In the Left-Handed co-ordinate system with increasing Y pointing upwards) have the greatest magnitude. The following code snippet should demonstrate what I mean.
if ((abs(cam_look_x)>abs(cam_look_z))
{
//camera X component is dominant
//making Y the best match.
}
else
{
//Y axis is dominant
//making X the best match.
} The next step is to determine the grid points that make up the visible surface. There are probably many ways of doing this. My approach (that I'm sure is not the most efficient) is to find a grid point that is visible and then step along the line best matching the X axis on the screen, I test each grid point by transforming it into screen space until I find the edges of the view port. I then step along the other map axis until I have built two arrays containing the grid points that are just off the screen at each side, the arrays stretch from just under the camera to whatever your chosen display distance is unless the top of the screen comes first.
Each pair of array entries will represent a line from the left hand side of the view port to the right hand side, this is really the key to the algorithm, we can use this to eliminate redundant edge scanning. We will be rendering the landscape using vertical strips rather than the horizontal strips more commonly found in polygon rendering. We now construct a table containing one entry for each vertical line on the screen. Each table entry will contain information concerning what has been drawn so far and where it has been drawn. We initialise the table with some relevant co-ordinates, the following sample code shows a possible declaration for the table as well as an initialisation function.
#define screenwidth 320 //width of the screen.(in pixels)
#define screenheight 200 //height of the screen (in pixels)
typedef struct {
int disp_height;
int last_height;
char *disp_pos;
int U,V;
} ytab_struct;
ytab_struct ytab[screenwidth];
void initialise_ytab()
{
ytab_struct *ytptr;
int ind;
ytptr = &ytab
for (ind=0;inddisp_height=screenheight;
ytptr->last_height=screenheight;
ytptr->U=ytptr->V=0;
ytptr->disp_pos=address_of_screen_ram + ind + (screenwidth*screenheight);
ytptr++;
}
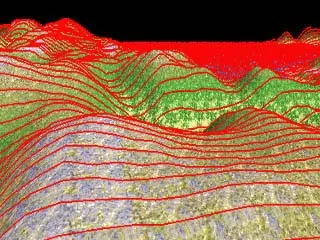
}For each pair of entries in the point array we should scan pixel by pixel from the left hand side to the right hand side of the screen, we should be looking at one point per vertical line. Between the transformed grid points we should interpolate the vertical position on the screen. It is also necessary to interpolate the U and V values for the grid points. This process is very similar to scanning an edge of a triangle or polygon although we have to do a separate 'edge' for each grid point that lies within the screen for the relevant line in the height field. If we were to plot the vertical position of each point as we perform the interpolation you should get a result something like the following image. The image has hidden lines removed for clarity.
Landscape plotted as scans.
We can now look at texture mapping. To texture map the landscape we simply take the newly interpolated values for Y, U and V and use them to draw a vertical line between the level of the relevant value for disp_height and the newly interpolated Y position. If the new Y value is less than the relevant disp_height then we know that the line segment is obscured by part of the landscape in front of it (or the base of the screen). After we have drawn the vertical line in a similar manner to scanning an internal line of a triangle we store the new Y position, U and V back into the table, we also update the values for disp_pos. In reality the entire process of interpolating across the screen and interpolating vertically up the screen will be done in a single assembler function for optimal performance, for the purpose of demonstration the following 'c' pseudo code fragment describes a function that is passed the vertical line position (as 'ind'), the newly interpolated Y position (as 'new_y') and the U & V co-ordinates.
void DrawVerticleStrip(int ind, int new_y, int U, int V)
{
int pos;
if (ytab[ind]->disp_height>=new_y)
{
//the line is totally obscured.
ytab[ind].last_height]=new_y;
ytab[ind].U=U;
ytab[ind].V=V;
return;
}
if (ytab[ind]->last_heightdisp_height=screenheight;
ytptr->last_height=screenheight;
ytptr->U=ytptr->V=0;
ytptr->disp_pos=address_of_screen_ram + ind + (screenwidth*screenheight);
ytptr++;
}
}If you have managed to keep up then you should now be seeing the benefits of this algorithm, we have completely eliminated overdraw within the landscape and there is no wasted edge scanning. The edge scanning is not only efficient but we have eliminated a significant amount of edge scanning that polygon based systems would need however efficient, but not without cost.
We now have a landscape that is texture mapped entirely with a singe bitmap, this is obviously quite limiting in many ways. We could try to texture map the landscape with one massive texture map but even a 4 megabyte texture map (2048 x 2048) would be inadequate if the height field was of any really usable size (see Possible Additions). Because of the manner we are texture mapping the landscape we cannot use a standard tile based texture mapping system to add detail since the algorithm prohibits us from determining the boundaries of the would be tiles. The solution that I use is to implement what I call 3 dimensional texture mapping.
[size="5"] 3 Dimensional Texture Mapping.
By layering multiple (but related) texture maps on top of each other we can create what I call a 3 dimensional texture map. Instead of using a rectangular bitmap that we address with U & V co-ordinate pairs we will have a texture cube that we address with U, V and W co-ordinates (with W addressing the layer). I originally looked at using these texture maps for simulating damage in a DOOM / QUAKE style engine, each of the layers would show a progression from say an undamaged wall through a cracked up wall through to a jumble of wires (or whatever you would suggest is underneath), I could then show damage to a wall by adjusting the W texture co-ordinate where damage occurs. Applying this to a landscape reveals a simple order for a potential 3 dimensional texture map, we can go from water through sand (or mud) onto grass and then onto rock and maybe snow. The image bellow shows a potential 3 dimensional texture map for a landscape.
A 64x64x32 3-dimensional Texture map.
[size="5"] Where Do We Get 'W' From?
Since we now need to address the texture map with an additional texture co-ordinate we need to know where to get this value from. It is a simple thing however to add the third texture co-ordinate to the above algorithm once we have it. The traditional way to determine from a landscape what is water, grass, rock etc. is to infer this information from the level described by the height field, this however limits us to a definite order to landscape detail. My preference is to provide an additional 'w' map similar to the original height map. We can create this 'w' map by starting with the height map and editing it to include the extra detail we want. We could for example add lakes half way up a mountain, you could also add a little bit of random noise to flat areas of the landscape so that it jitters between similar textures in order to break up the texture maps.
The image underneath shows the final landscape with the 3 dimensional texture map applied. The version of the code that rendered this included some subtle lighting as well.
The final rendered image, with some subtle lighting.
The same image with the horizontal Scans superimposed.
[size="5"] LimitationsIt is very difficult to add detail not included in the 3 dimensional texture map, if for example you wanted to add a road this could only be done by either overlaying polygons containing road detail or by using one of the existing texture's with the associated blending out to the surrounding texture map.
When the camera turns to a point where the dominant axis changes there is a slight visible jump. this can be reduced by scanning the height field at 45 degree angles as well as along the primary axis but this will only reduce the jump, it will never eliminate it entirely.
The landscape gets its speed and efficiency by not using triangles or polygons. This however introduces a problem if you wish to also make use of hardware accelerators. I hope to cover methods of rendering this kind of landscape using hardware accelerators in a future document.
Despite camera tilt not being a requirement the system can render tilted cameras but only to a limited angle. This can be increased by creating multiple render routines that render in directions different to bottom-up.
[size="5"] Possible Additions
One method of circumnavigating the problem of additional detail (and maybe introducing a little extra speed) would be to go back to using a single large texture map. Instead of trying to produce a single texture map that covers the entire landscape, we only concern our selves with a section localised around the current camera location. By operating a large texture (perhaps 1024x1024 = 1 megabyte) as a sliding window as we move around the landscape we can add whatever additional detail we require as we go. As the camera moves we would modify the data at the edges of the sliding window probably using the 3 dimensional texture map approach as a base and then adding roads and lighting on top. Any additional data could be added at this time with little cost to the render time. In a game environment it may be possible to add damage, scorch marks and tire marks on the fly to the temporary texture map, we would lose them if we moved away sufficiently from the area and then returned but who cares in a game?