...the time taken scales linearly with the number of nops in the sequence, so they'd be O(N)
You're going to confuse him, lol. Any constant time process repeated N times is O(N). nop itself is O(1).
Would a statement that has no effect (which the compiler optimizes out) count as O(0)?
That would be an understandable way of looking at it, but big-O is used to measure algorithmic complexity rather than compiler behavior. Like Hodge said, O(0) means 'this process has zero complexity in all cases'. It's a sort of "What is the sound of one hand clapping?" kind of thing.
EDIT:
Looking at Properties / Multiplication by a constant on the Wiki page:
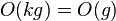 if k is nonzero
if k is nonzero
Assuming g = 1, this would translate to O(k) = O(1). It is explicitly stated that k must be nonzero, but in order for O(0) = O(1) being true, that would have to be the case.
Now don't ask me why k must be nonzero, but presumably it's just for that reason.
Wait... of course k must be non-zero... otherwise you could magically turn any O(nx) algorithm into O(1) and the whole thing wouldn't make sense any more...
It would make sense because if k were zero then you'd be doing no work, so you'd have no complexity. It would be O(0). The reason non-zero values simply drop the k is that complexity is concerned with growth rates rather than direct measurements. This is a measure of how the performance will change as the size of the set increases:
k = 1
O(kN)
When N goes from 1 to 10 complexity increases (1 to 10) by a factor of 10. The rate of change is linear.
k = 5
O(kN)
When N goes from 1 to 10 the complexity increases (5 to 50) by a factor of 10. The rate of change is linear.
The constant k is irrelevant to the rate of change as N increases. However, if k is zero then no work is done, regardless of the set size, so we get O(0).
A programming example. Let's say k is the time it takes some process to work on an array of size N:
array someArray[N];
/////////////////////measuring the complexity of this section
for(item in someArray) {
//do constant 'k' amount of work
}
/////////////////////end section
If k is one second then an array with 60 members takes one minute to process. If we double the array size, the time doubles, etc. This is linear complexity: O(N). The k is irrelevant.
However, what if we remove the loop? Now k is zero, and it turns out our complexity is also zero, because no matter the size of the array we do no work on it. This is O(0).


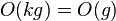 if k is nonzero
if k is nonzero



