Quote: Original post by owl
I even remember my dad telling me (when I was just a kid) to take a string and measure a circle to see how much it's length was, and, if I'm not wrong, measuring with physical objects still gives a values closer to 3.14etc than 4.

Closer to pi, but not pi as it is mathematically defined, even if you somehow were to eliminate measurement errors, since the geometric definition of pi demands a perfectly flat euclidian space, something which you are not in.

Quote: Original post by Eelco

Quote: Original post by nilkn

Quote: Original post by szecs
I'm pretty sure it should be easy to explain with mathematics (convergence, "lim" stuff and formulas), but I want to be convinced with simple GEOMETRY. Just like Archimedes would. So that I can IMAGINE it.

I feel it has to so something with fractal geometry, but this thinking ("we can construct an object that looks like a line blah blah") seems to be too "reverse thinking" to me. I don't feel that warm "I'm convinced" feeling.

But maybe I'm trolling myself.

It seems to me the most evident geometric reason is that the tangents to the limit curve--the circle--exhibit all possible directions while the tangents to the zig-zag curves are always either horizontal or vertical. This is the basic geometric issue which prevents the limit machinery from working out as you would expect.

I pointed it out earlier in this thread, but since you mentioned Archimedes I'll say it again. The issue I just described does not occur when you use circumscribed n-gons like Archimedes did.

In the present example, we have uniform convergence of curves to a limit without convergence of the derivatives. In Archimedes' examples, we have both convergence of curves to a limit and convergence of the derivatives.

'the derivatives'? Only the zero'th and first, actually. That still leaves the nagging question as to why it is only those two that matter.

I don't understand what you mean.

You have a sequence of curves. Each curve has a derivative. Those derivatives form a sequence of functions. That's what I was referring to.

Quote: Original post by nilkn

Quote: Original post by Eelco

Quote: Original post by nilkn

Quote: Original post by szecs
I'm pretty sure it should be easy to explain with mathematics (convergence, "lim" stuff and formulas), but I want to be convinced with simple GEOMETRY. Just like Archimedes would. So that I can IMAGINE it.

I feel it has to so something with fractal geometry, but this thinking ("we can construct an object that looks like a line blah blah") seems to be too "reverse thinking" to me. I don't feel that warm "I'm convinced" feeling.

But maybe I'm trolling myself.

It seems to me the most evident geometric reason is that the tangents to the limit curve--the circle--exhibit all possible directions while the tangents to the zig-zag curves are always either horizontal or vertical. This is the basic geometric issue which prevents the limit machinery from working out as you would expect.

I pointed it out earlier in this thread, but since you mentioned Archimedes I'll say it again. The issue I just described does not occur when you use circumscribed n-gons like Archimedes did.

In the present example, we have uniform convergence of curves to a limit without convergence of the derivatives. In Archimedes' examples, we have both convergence of curves to a limit and convergence of the derivatives.

'the derivatives'? Only the zero'th and first, actually. That still leaves the nagging question as to why it is only those two that matter.

I don't understand what you mean.

You have a sequence of curves. Each curve has a derivative. Those derivatives form a sequence of functions. That's what I was referring to.

Emphasis mine. The second derivative and upwards are all zero for a polygon, so they do not converge at all.

I wasn't talking about second and higher derivatives. Is your question why one needs the convergence of the sequence of first derivatives in order for arc length to commute with the limit operation but one does not need convergence of higher derivatives? The answer to that is probably that only first derivatives are necessary to compute arc length.

Quote: Original post by nilkn
I wasn't talking about second and higher derivatives. Is your question why one needs the convergence of the sequence of first derivatives in order for arc length to commute with the limit operation but one does not need convergence of higher derivatives?

Yes

Quote: The answer to that is probably that only first derivatives are necessary to compute arc length.

Thats a good one; it completes the answer to the general question of what sets working and non-working methods apart.

Indeed convergence of tangent direction of the curves is necessary as well, because the arc length formula says so.

Quote: Original post by Fenrisulvur
I'm not exactly sure which terms and notation you're taking as "common", here, or in what sense. Are you rejecting structure like metric spaces and definitions like that of the circle I gave in favour of some unstated common-sense interpretation, or are you familiar with such structural abstractions and objecting to having it all rehashed?

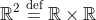
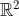
More the latter. For example, this says the same thing in three ways: "the set of ordered pairs of real numbers, in other words ". What seems strange to me is that I believe the first would reach the largest audience since the Cartesian product is likely to be introduced later in any math program. It's maybe justified by the use of in the mapping notation to make the connection more immediate, but functional notation with implicit (co)domain and range would've worked as well.

Quote:

Quote: Original post by Way Walker
(you even got fed up with it and just said you would be using "vector space axioms", which usually goes without saying)

Oh, no it doesn't. That line would've been torn apart in a more formal setting, I hadn't defined any structure other than a metric at that point. Do you have any idea how many vector spaces can be constructed on R*R?

How many are isomorphic? Or, more to the point, how many are isomorphic to the Euclidean space?

Quote:
I maintain that an answer to the troll's paradox is going to have to be structural, it's going to have to illuminate criteria which govern whether a sequence of bounding shapes do or do not coverge to give the circumference of the circle, and we're probably going to need a formal definition of what a circumference actually is.

I agree, but the simplest definition would be to simply integrate the length along the curve.

Quote: Original post by JoeCooper
I don't think we could possibly have a procedure that can validate any and all possible shapes you could throw at it, for all manner of procedures, with my philosophy-student level math.

Maybe true, maybe not. I was hoping something would come out of the discussion. [smile]

Quote:
As I understood the specifications originally, all I felt I needed to do was to show that this particular gizmo isn't approximating a circle.

Actually, the problem is that it is approximating a circle (defined as the set of points) but not all of its properties are good approximations of the properties of a circle. In particular, the perimeter, but also, for example, the first derivative. The n-gon method also doesn't provide good approximations of all the properties of a circle, like the second derivative.

Quote:
I don't mean this to sound hostile in any way, but you seem confident that you have a superior handle on the maths to everyone else - why not pitch a fitness test?

Doesn't seem hostile and I almost certainly don't have a superior handle on the math. For one thing, I know very little about fractals.

I've been trying to think of a good fitness test, but I'm having trouble finding a necessary condition. One problem being that the limit of the derivative is not just incorrect, but undefined.

Quote: Original post by Eelco
'the derivatives'? Only the zero'th and first, actually. That still leaves the nagging question as to why it is only those two that matter.

On a more generic level to nilkn's answer, the different derivatives have different meanings. Having a continuous first derivative makes a function smooth, so, since the lack of smoothness is part of the problem, it wouldn't be a surprise if the first derivative is important. Likewise, if curvature isn't an issue, then the second derivative probably isn't important.

Quote:
Emphasis mine. The second derivative and upwards are all zero for a polygon, so they do not converge at all.

Technically, they do converge, just not to the same value as the derivatives of the figure the polygons converge to. I wonder if they have to converge to the same value, or if convergence is enough (e.g. it just needs to be smooth). Of course, I'm not sure that you can have the zeroth derivative converge to the right value and the first derivative converge without the first derivative converging to the right value.

Can maybe you explain this in a different way? If the problem is that there is smaller areas between the circle and fractal, why doesn't the approximation get better as we approach infinity?

because it never shortens the path, but always just redirects it. as such, it can never change a value.

it would, though, get close to the area.

The definition "all points with a distance r" is not very useful in the context of the circumference because it defines a set and there is no such thing as the "length of a set". So usually when we speak about the circumference we mean the length of a closed curve which is given by arc length, which is only defined for differentiable curves. The proposed approximating curves are only piecewise differentiable which still allows to "extend" the notion of length. But here is the kicker: the proposed sequence of curves does not converge in the space of piecewise differential curves since the limit isn't piecewise differentiable (there are more than finitely many discontinuities). So technically the limit diverges.

Another way to look at it is that this approach measures the length of the circle in the "Manhattan metric" which is obviously not the same as the euclidean metric, so Pythagoras probably has no problem at all since you use another space than he does. In a spherical geometry for example the radius and circumference aren't even directly proportional (pi is a function of r if you will).

oy, all this discussion over a misunderstanding of what was being measured? The pic is just adding bounding limits (or a way to approximate area by squares), not the circle's perimeter. Its a trig-trick-problem. That is why it approximates to 4 all the time. To measure the perimeter, you have to use the hypoteneuse of the cut corners + sides. If you don't, No mater how far you derive it down, it will always be over-measuring the distance of the length between the two straight-edges (circle side), hence it approximates to 4, not half-tau (pi).

The diagonal paradox has always been always been an issue with human perception of segmentation and understanding of infinite approximation. One thinks they are measuring a diagonal, but they are not, they are still just measuing the original verticals and horizontals (they just cant see the segmentation combined with the interweave), so they infer diagonal measurement when there never was any cause to do so. This is also backed up by the fact they never stopped measuring the original lengths/structure to begin with (i.e., you can divide a line an infinite number of times, but the sum of its segments length is still the same as the original line).

To measure the perimeter, you have to use the hypoteneuse of the cut corners...

And now explain why a polygonal approximation is "more valid" than the proposed version .