So I think it's about time I talk about that secret super-duper technique I was going to talk about, but said I would post elsewhere first, because it was so good. I'm already satisfied with how things are going (in other areas), so I don't mind posting it. I made all these screenshots and methods in 2016.
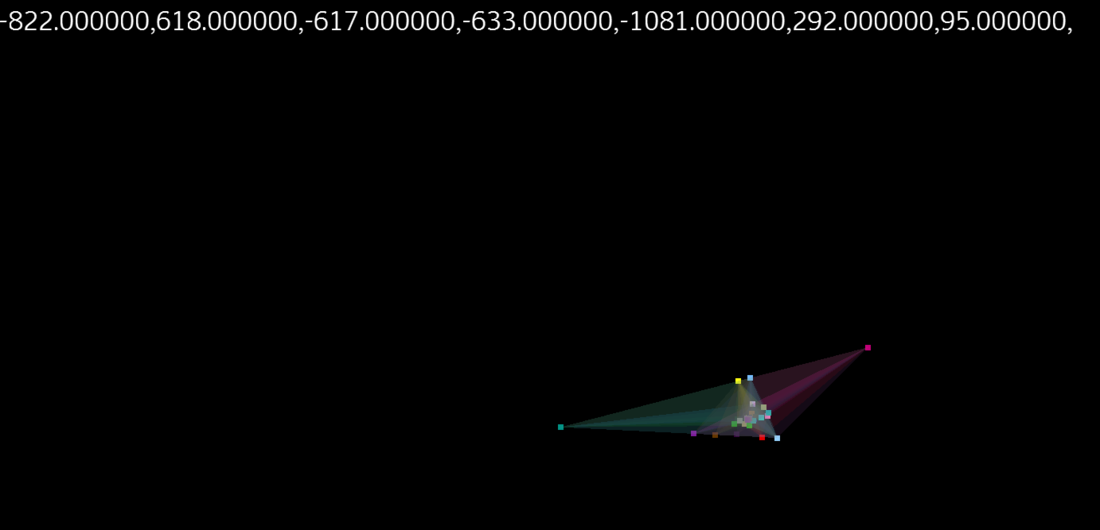
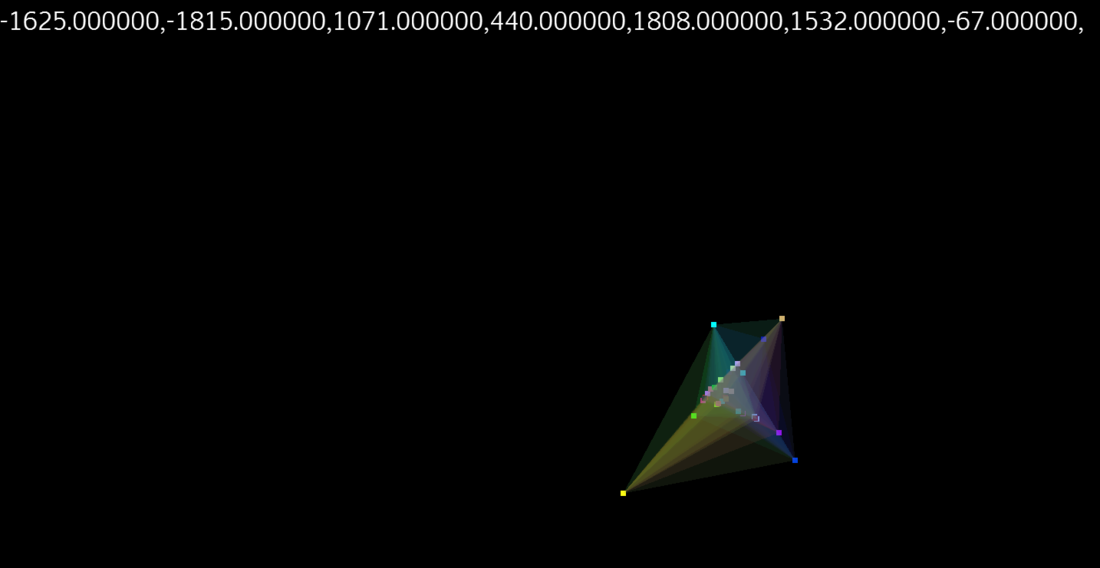
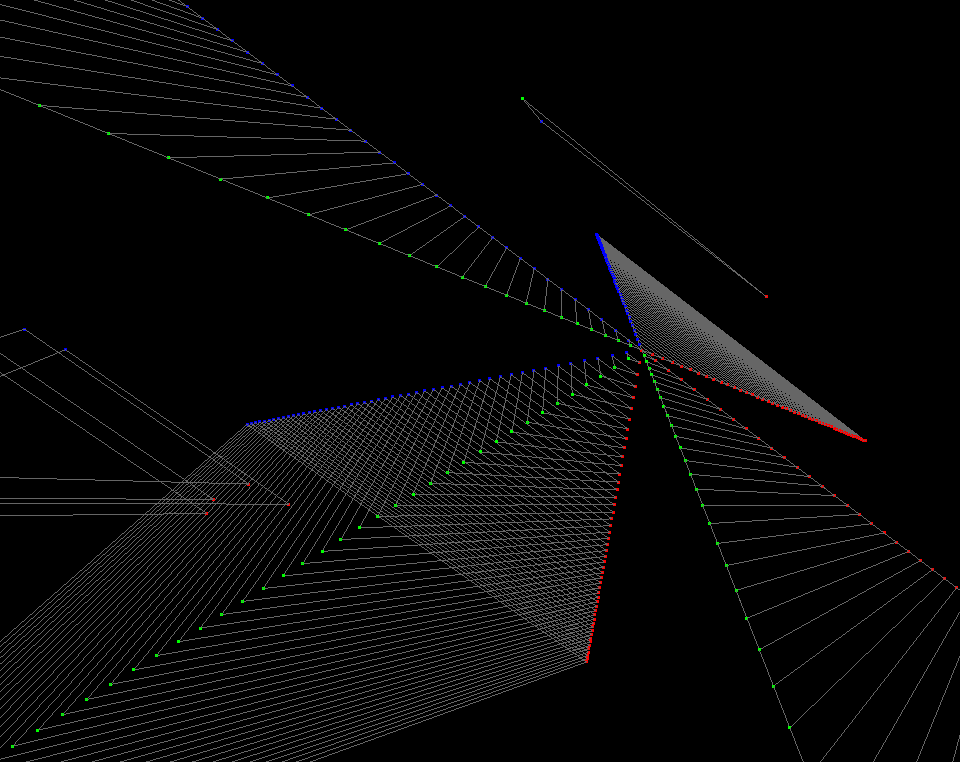
I was wrong in the screenshots with only 1 prism and 3 triangles, as that means only 3 3-plane point intersections from a total of 4 planes. There should actually be 4 3-plane point intersections from them: 123, 124, 134, 234
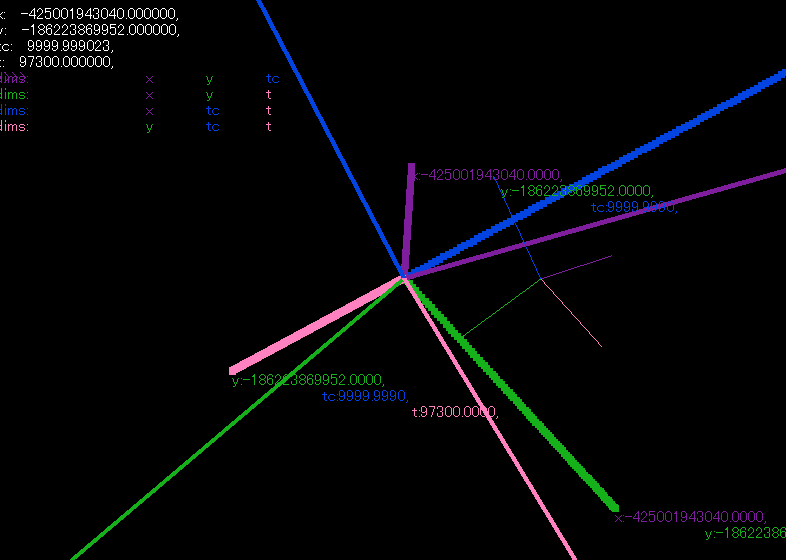
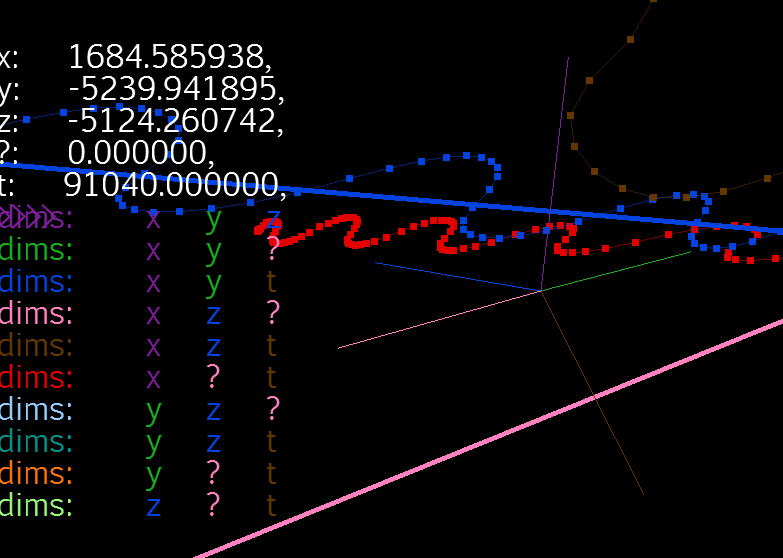
The basic idea is we can think of any point in any dimensional space using axes as one of either two things. 1.) The simple case is that a point is the vector components (coordinates) along each axis added together to make one vector and thus point. But, 2.) equivalently in 3D and lower spaces as expressed in our 3D space world, but not equivalent in higher dimensional spaces, expressed in our 3D space world, we can also think of the 3-point(s) as the intersections of the hyper-planes (3D normal vector + distance) where each plane is at a distance along the axis (which are skewed, to fit all together in a 3D space representation) and the normal is obtained by the direction of that (skewed) axis vector. The result is 4 3-point intersections for 4D space, and 15 3-point intersections for 7D space, etc. The skewed axes can also be used with method #1, but with addition of a vector along the skewed axes.
You can use the axes for whatever you want: x,y,z,t or mass or acceleration components. It can be connected together in 7D or other dimensions to form a shape. It is best in some cases (#1 but not really #2) to choose skewed axes that don't counteract each other in opposite directions, so that less space is shared, however it is unavoidable with method #1 but method #1 is the one that will give a single-point intersection.